2020—2021学年人教版高一数学《两条平行直线间的距离》课件(19张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《两条平行直线间的距离》课件(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 335.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 08:40:10 | ||
图片预览



文档简介
3.3.4 两条平行直线间的距离
掌握两条平行线间的距离公式(重点),并会灵活应用(难点).
新课导入
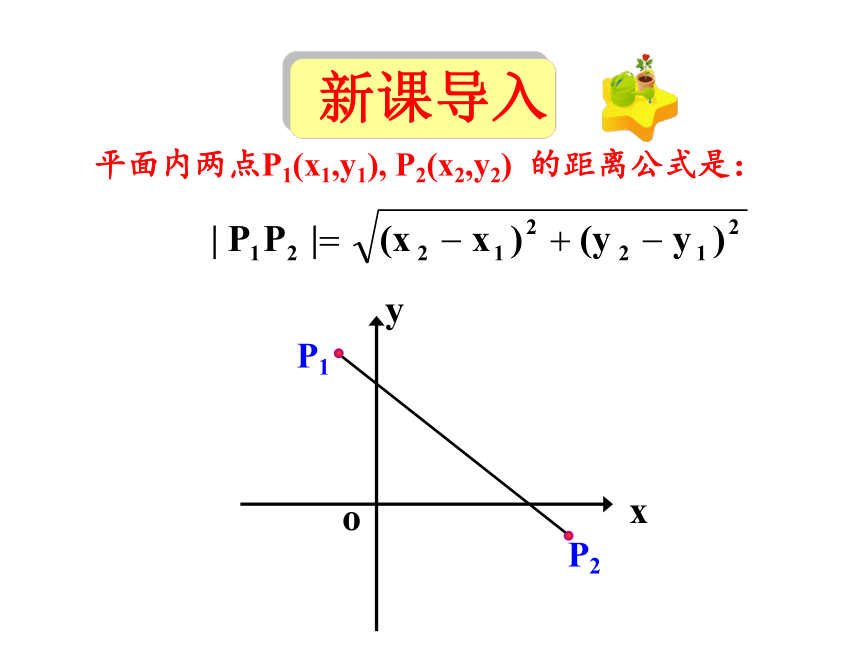
平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是:
y
x
o
P2
P1
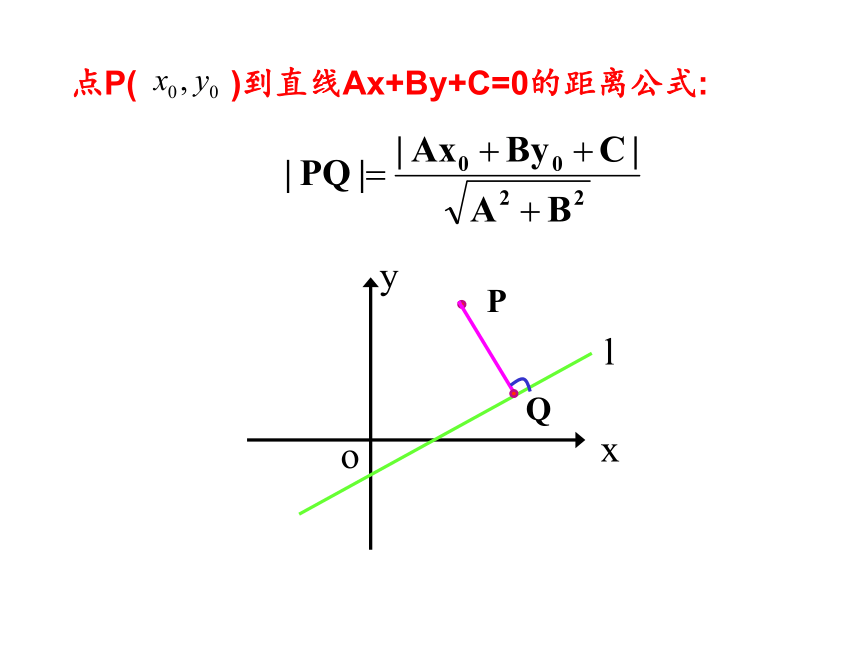
Q
P
y
x
o
l
点P( )到直线Ax+By+C=0的距离公式:
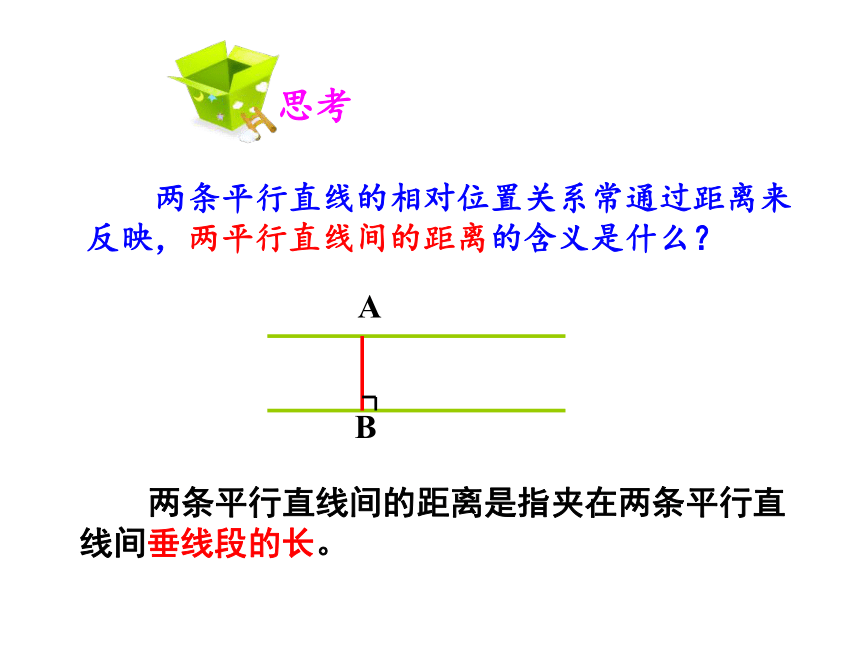
两条平行直线的相对位置关系常通过距离来反映,两平行直线间的距离的含义是什么?
思考
A
B
两条平行直线间的距离是指夹在两条平行直线间垂线段的长。
A
B
A1
B1
A2
B2
夹在两条平行直线间垂线段的长相等。
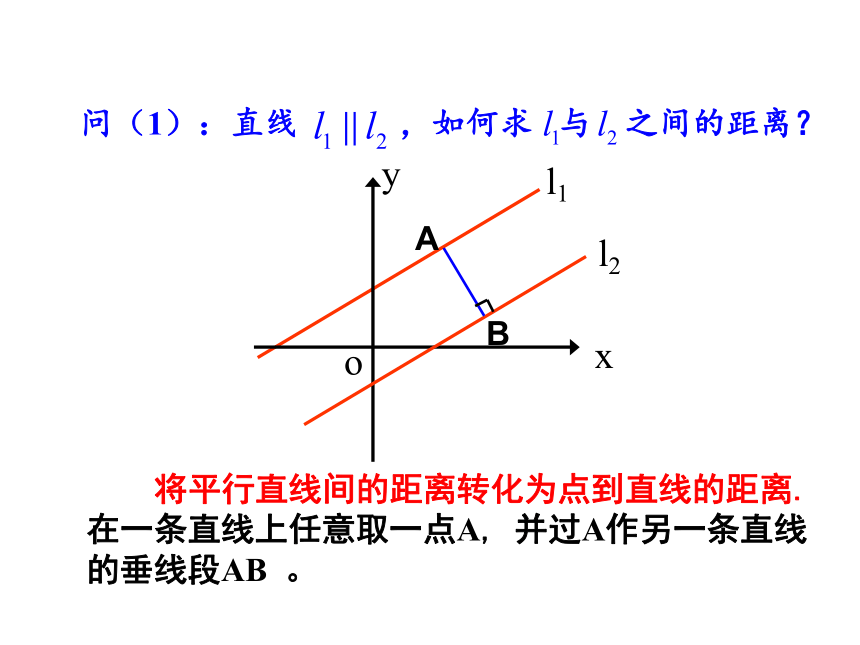
问(1):直线 ,如何求 与 之间的距离?
将平行直线间的距离转化为点到直线的距离.在一条直线上任意取一点A, 并过A作另一条直线的垂线段AB 。
y
x
o
l2
l1
A
B
问(2):如何取点,可使计算简单?
y
x
o
l2
l1
A
B
A
B
A点取在 与坐标轴的交点时,计算较为简单。
求平行线 2x-7y+8=0 和 2x-7y-6=0 的距离。
解: 在直线 2x -7y -6=0 上取 P( 3, 0), 则 P( 3, 0)到
直线 2x -7y +8 =0 的距离就是两平行线间的距离。
例题分析
问(3):你能根据上述例题,探究Ax+By+C1=0与Ax+By+C2=0这两条直线间的距离是多少?
两条直线的系数有什么特点?
y
x
o
l2
l1
A
B
在l1与x轴交点处取 ,A点到 的距离
由于两平行直线l1和l2的斜率k1=k2,所以两直线必可写成Ax+By+C1=0与Ax+By+C2=0的形式,所以可以用公式:
该公式用来计算两平行直线间的距离。
注意:两直线方程中A,B系数分别相同。
例1.
变式1:求下列两条平行线间的距离:
(1) ;
(2) ;
例2.
求与直线l:5x-12y+6=0平行,且到l得距离为2的直线的方程。
解:设所求直线为5x-12y+C=0,
所求直线为5x-12y-20=0或5x-12+32=0。
即|6-C|=26,解得C=-20或32。
变式2:已知到两条平行直线2x-y+2=0和直线2x-y+4=0的距离相等的直线方程为________.
例3.
课堂小结
法一:可将求平行直线间的距离
转化为求点到直线的距离。
y
x
o
l2
l1
A
B
法二:两条平行线Ax+By+C1=0
与Ax+By+C2=0的距离是
随堂练习
布置作业
课本:P116习题3.3
A组 10、
P120 A组 10、11
P120 B组 4
掌握两条平行线间的距离公式(重点),并会灵活应用(难点).
新课导入
平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是:
y
x
o
P2
P1
Q
P
y
x
o
l
点P( )到直线Ax+By+C=0的距离公式:
两条平行直线的相对位置关系常通过距离来反映,两平行直线间的距离的含义是什么?
思考
A
B
两条平行直线间的距离是指夹在两条平行直线间垂线段的长。
A
B
A1
B1
A2
B2
夹在两条平行直线间垂线段的长相等。
问(1):直线 ,如何求 与 之间的距离?
将平行直线间的距离转化为点到直线的距离.在一条直线上任意取一点A, 并过A作另一条直线的垂线段AB 。
y
x
o
l2
l1
A
B
问(2):如何取点,可使计算简单?
y
x
o
l2
l1
A
B
A
B
A点取在 与坐标轴的交点时,计算较为简单。
求平行线 2x-7y+8=0 和 2x-7y-6=0 的距离。
解: 在直线 2x -7y -6=0 上取 P( 3, 0), 则 P( 3, 0)到
直线 2x -7y +8 =0 的距离就是两平行线间的距离。
例题分析
问(3):你能根据上述例题,探究Ax+By+C1=0与Ax+By+C2=0这两条直线间的距离是多少?
两条直线的系数有什么特点?
y
x
o
l2
l1
A
B
在l1与x轴交点处取 ,A点到 的距离
由于两平行直线l1和l2的斜率k1=k2,所以两直线必可写成Ax+By+C1=0与Ax+By+C2=0的形式,所以可以用公式:
该公式用来计算两平行直线间的距离。
注意:两直线方程中A,B系数分别相同。
例1.
变式1:求下列两条平行线间的距离:
(1) ;
(2) ;
例2.
求与直线l:5x-12y+6=0平行,且到l得距离为2的直线的方程。
解:设所求直线为5x-12y+C=0,
所求直线为5x-12y-20=0或5x-12+32=0。
即|6-C|=26,解得C=-20或32。
变式2:已知到两条平行直线2x-y+2=0和直线2x-y+4=0的距离相等的直线方程为________.
例3.
课堂小结
法一:可将求平行直线间的距离
转化为求点到直线的距离。
y
x
o
l2
l1
A
B
法二:两条平行线Ax+By+C1=0
与Ax+By+C2=0的距离是
随堂练习
布置作业
课本:P116习题3.3
A组 10、
P120 A组 10、11
P120 B组 4
