2020—2021学年人教版高一数学《圆与圆的位置关系》课件(18张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《圆与圆的位置关系》课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 08:41:52 | ||
图片预览






文档简介
圆与圆之间的位置关系
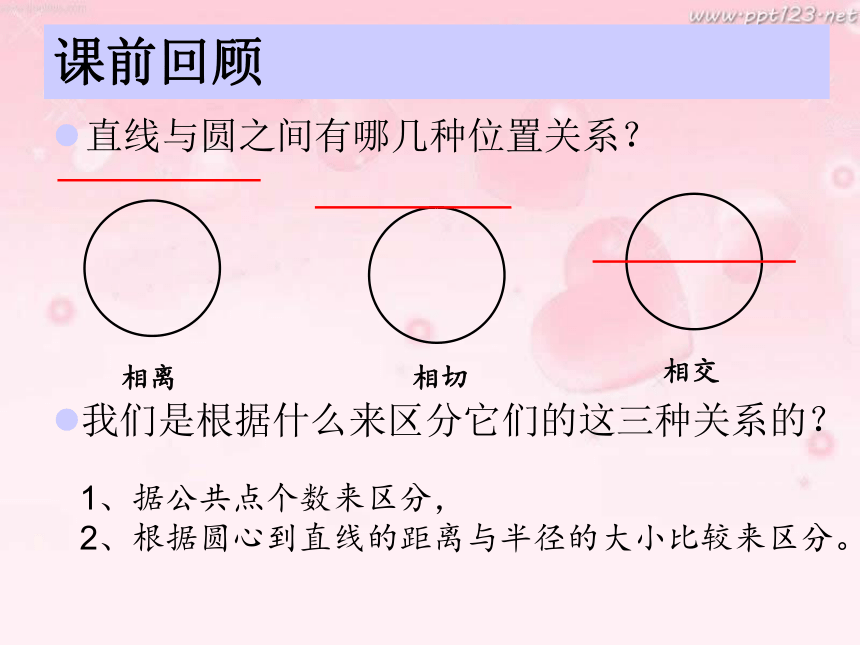
课前回顾
直线与圆之间有哪几种位置关系?
我们是根据什么来区分它们的这三种关系的?
相交
1、据公共点个数来区分,
2、根据圆心到直线的距离与半径的大小比较来区分。
相离
相切
思考
如果把这里的直线改为圆,则圆与圆之间又会有什么样的位置关系呢?我们又可以根据什么来区分它们的这些位置关系呢?
观察
观察
观察
实验探究
圆与圆的位置关系如下:
观察两圆的这五种关系,你能说出它们各自有什么特点吗?比如公共点的个数以及一个圆上的点
在另一个圆的内部还是外部?
小结
相离
(没有公共点)
相切
(一个公共点)
相交
(两个公共点)
外离
内含
相交
外切
内切
一个圆上的所有点都在
另一个圆的外部
一个圆上的所有点都
在另一个圆的内部
除公共点外,一个圆上
的点都在另一个圆的
外部
除公共点外,一个圆上
的点都在另一个圆的
内部
一个圆上的点有的在
另一个圆的内部,有
的在另一个圆的外部
想一想
问题1:圆是轴对称图形吗?
它的对称轴是什么呢?
是,对称轴是任何一条
直径所在的直线。
问题2:圆与圆组成的图形呢?
也是轴对称图形,对称轴是
通过两个圆的圆心的直线。
对称轴
认识连心线:
通过两圆圆心的直线叫做连心线。连心线上两圆心的距离叫做圆心距。
连心线是两圆组成的图形的对称轴。
根据对称性可知,如果两圆相切,则切点一定在连心线上。
如果大圆半径为R,小圆半径为r,圆心距为d。则在五种情况下三者之间有什么样的数量关系呢?
(1)外离
(2)内含
(3)外切
(4)内切
(5)相交
总结
圆的五种位置关系
外离
内含
内切
无公共点,一个圆上的所有点都
在另一个圆的外部
无公共点,一个圆上的所有点都在另一个圆的内部
两个公共点,一个圆上的点有的在另
一个圆的内部,有的在另一个圆的外部
一个公共点,除公共点外,一个圆上
的点都在另一个圆的内部
一个公共点,除公共点外,一个圆上的点都在另一个圆的外部
相交
外切
将这五种数量关系用数轴表示为
思考题:相交时, 只有一边的条件能判断两圆相交吗?
2.已知⊙1和⊙2的半径分别为5cm和3cm,如果⊙1和⊙2相切,则圆心距=
练一练
1.在图中有两圆的多种位置关系,请你找出 还没有的位置关系是 .
8或2
相交
思考5:判断圆与圆的位置关系的方法的操作步骤:
代数法:
1.将圆C1与圆C2方程联立成方程组;
2.通过减法消元,得到一个 二元一次方程,通过代入消元法得到一个一元二次方程
3.求出其判别式△的值;
若△>0,则直线与圆相交;
若△=0,则直线与圆相切;
若△<0,则直线与圆相离.
几何法:
1.由圆的方程一般式,求出圆心坐标和半径R和r;
2.利用点到点的距离公式求圆心间的距离d;
3.比较d与R+r,R-r的大小关系:
恳请老师给予点评和指导
课前回顾
直线与圆之间有哪几种位置关系?
我们是根据什么来区分它们的这三种关系的?
相交
1、据公共点个数来区分,
2、根据圆心到直线的距离与半径的大小比较来区分。
相离
相切
思考
如果把这里的直线改为圆,则圆与圆之间又会有什么样的位置关系呢?我们又可以根据什么来区分它们的这些位置关系呢?
观察
观察
观察
实验探究
圆与圆的位置关系如下:
观察两圆的这五种关系,你能说出它们各自有什么特点吗?比如公共点的个数以及一个圆上的点
在另一个圆的内部还是外部?
小结
相离
(没有公共点)
相切
(一个公共点)
相交
(两个公共点)
外离
内含
相交
外切
内切
一个圆上的所有点都在
另一个圆的外部
一个圆上的所有点都
在另一个圆的内部
除公共点外,一个圆上
的点都在另一个圆的
外部
除公共点外,一个圆上
的点都在另一个圆的
内部
一个圆上的点有的在
另一个圆的内部,有
的在另一个圆的外部
想一想
问题1:圆是轴对称图形吗?
它的对称轴是什么呢?
是,对称轴是任何一条
直径所在的直线。
问题2:圆与圆组成的图形呢?
也是轴对称图形,对称轴是
通过两个圆的圆心的直线。
对称轴
认识连心线:
通过两圆圆心的直线叫做连心线。连心线上两圆心的距离叫做圆心距。
连心线是两圆组成的图形的对称轴。
根据对称性可知,如果两圆相切,则切点一定在连心线上。
如果大圆半径为R,小圆半径为r,圆心距为d。则在五种情况下三者之间有什么样的数量关系呢?
(1)外离
(2)内含
(3)外切
(4)内切
(5)相交
总结
圆的五种位置关系
外离
内含
内切
无公共点,一个圆上的所有点都
在另一个圆的外部
无公共点,一个圆上的所有点都在另一个圆的内部
两个公共点,一个圆上的点有的在另
一个圆的内部,有的在另一个圆的外部
一个公共点,除公共点外,一个圆上
的点都在另一个圆的内部
一个公共点,除公共点外,一个圆上的点都在另一个圆的外部
相交
外切
将这五种数量关系用数轴表示为
思考题:相交时, 只有一边的条件能判断两圆相交吗?
2.已知⊙1和⊙2的半径分别为5cm和3cm,如果⊙1和⊙2相切,则圆心距=
练一练
1.在图中有两圆的多种位置关系,请你找出 还没有的位置关系是 .
8或2
相交
思考5:判断圆与圆的位置关系的方法的操作步骤:
代数法:
1.将圆C1与圆C2方程联立成方程组;
2.通过减法消元,得到一个 二元一次方程,通过代入消元法得到一个一元二次方程
3.求出其判别式△的值;
若△>0,则直线与圆相交;
若△=0,则直线与圆相切;
若△<0,则直线与圆相离.
几何法:
1.由圆的方程一般式,求出圆心坐标和半径R和r;
2.利用点到点的距离公式求圆心间的距离d;
3.比较d与R+r,R-r的大小关系:
恳请老师给予点评和指导
