1.2.2 直角三角形全等的判定(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 1.2.2 直角三角形全等的判定(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 476.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 11:05:21 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学下册第1章三角形的证明
1.2
直角三角形
第2课时
直角三角形2
【知识清单】
1、判定两个直角三角形全等的方法有HL、SSS、SAS、ASA、AAS
;
2、证明两个直角三角形全等的思路:首先考虑利用HL定理,再考虑利用一般的三角形全等的证明方法.
【经典例题】
例题1、已知:如图,∠ACB=∠ADB=90°,AC=AD,E在AB上.求证:CE=DE.
【考点】直角三角形全等的判定方法.
【分析】先利用HL判定Rt△ABC≌Rt△ABD,从而得到对应角相等,对应边相等,再利用SAS判定△BEC≌△BED,从而得到CE=DE.
【解答】证明:∵∠ACB=∠ADB=90°,
在Rt△ABC和Rt△ABD中,
AC=AD,AB=AB,
∴Rt△ABC≌Rt△ABD(HL).
∴∠ABC=∠ABD.
BC=BD.
在△BEC和△BED中,
BC=BD,∠ABC=∠ABD,BE=BE,
∴△BEC≌△BED(SAS),
∴CE=DE.
【点评】本题考查三角形全等的判定方法,判定两个直角三角形全等时,首先考虑HL定理,再考虑一般方法有:SSS、SAS、AAS.
例题2、(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.
【考点】?直角三角形全等的判定;全等三角形的性质.
【分析】根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AE=AD+DE,所以BD=DE+CE;
根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AD+AE=BD+CE,所以BD=DE-CE.
【解答】(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE-CE;
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵AB=AC,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE-CE.
【点评】此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS,SAS,
ASA,AAS等.这种类型的题目经常考到,要注意掌握.
【夯实基础】
1、已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和?△DEF全等
的是(??
?)?
A.AB=DE,AC=DF??????
???B.AC=EF,BC=DF?
C.AB=DE,BC=EF????????
??D.∠C=∠F,BC=EF
2、如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据
是(
)
A.HL
B.AAS
C.SSS
D.ASA
3、在直角三角形中,其中一个锐角是另一个锐角的3倍,则此三角形中最小的角是(
)
A.15°
B.22.5°
?C.30°?
D.45°
4、要判定两个直角三角形全等,下列说法正确的有(?
?)?
①有两条直角边对应相等;?②有两个锐角对应相等;?③有斜边和一条直角边对应相等;
?④有一条直角边和一个锐角相等;?⑤有斜边和一个锐角对应相等;??⑥有两条边相等.?
??A.6个
B.5个
C.4个
D.3个
5、如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加
一个适当的条件:
,(答案不唯一),使△ADB≌△CEB.
6、如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要
添加的一个条件是
.
7、如图,在Rt△ABC中,AC⊥AB,垂足为A,AD⊥BC,垂足为D,∠1=∠2,有下列结
论:①AB∥DE;②∠B=∠3;③∠C=∠1;④∠B与∠2互余;⑤∠3=∠2.其中正确的
有
(填写正确的序号).
8、在△ABC中,高AD和BE交于F点,且AC
=BF,求:∠ABC的度数.
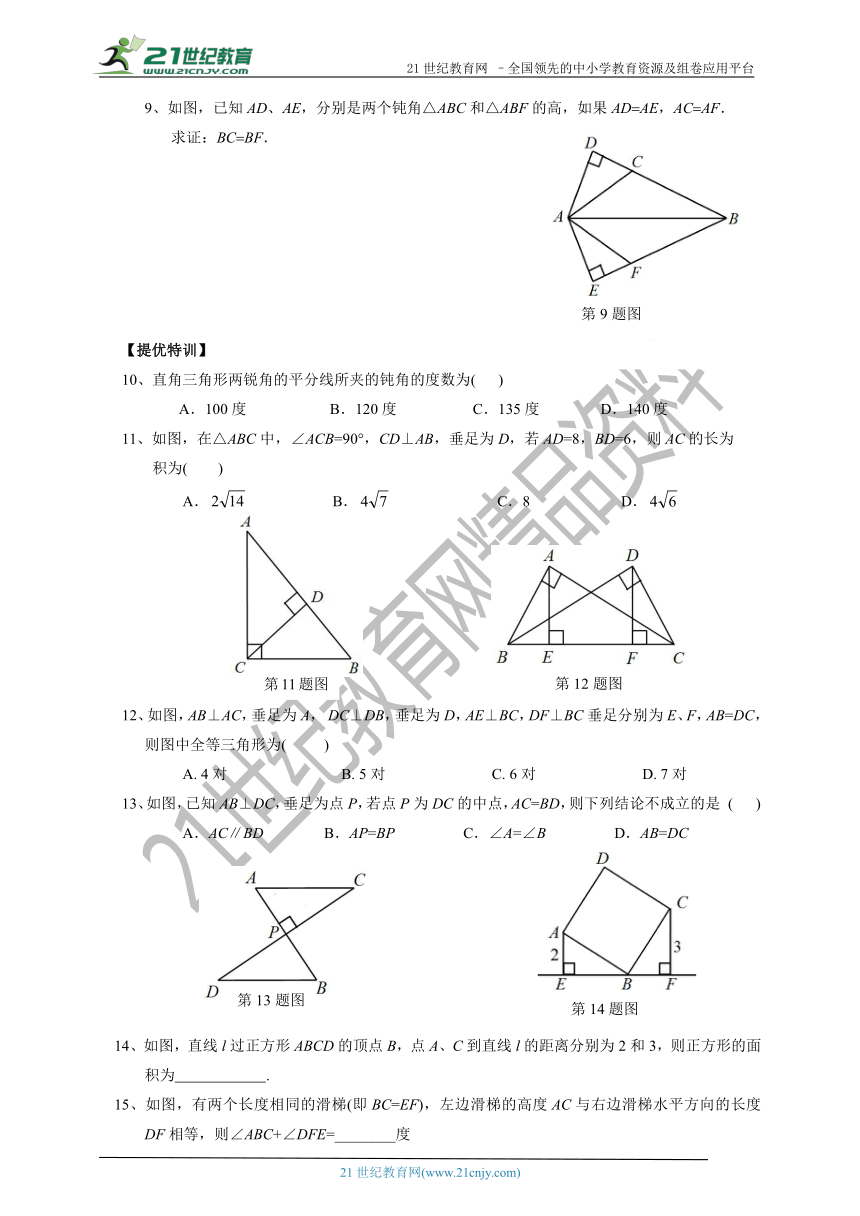
9、如图,已知AD、AE,分别是两个钝角△ABC和△ABF的高,如果ADAE,ACAF.
?
求证:BCBF.
【提优特训】
10、直角三角形两锐角的平分线所夹的钝角的度数为(
)
?A.100度
B.120度
C.135度
D.140度
11、如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AD=8,BD=6,则AC的长为
积为(
)
A.
B.
C.8
D.
12、如图,AB⊥AC,垂足为A,
DC⊥DB,垂足为D,AE⊥BC,DF⊥BC垂足分别为E、F,AB=DC,则图中全等三角形为(
)
A.
4对
B.
5对
C.
6对
D.
7对
13、如图,已知AB⊥DC,垂足为点P,若点P为DC的中点,AC=BD,则下列结论不成立的是
(
)
A.AC∥BD
B.AP=BP
C.∠A=∠B
D.AB=DC
14、如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的面积为
.
15、如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=________度
16、如图,在四边形ABCD中,∠B=∠D
=90°,∠BAD=135°,若AD=4cm,BC=10cm则四边形ABCD的面积为
cm?2.
17、如图,在△ABC与△ADE中,AB=AC,AD=AE,连接BE、CD,若∠ABE=∠ACD=90°,
求证:OD=OE.
18、如图,在△ABC中,BC=12,AB=2AC,D为BC延长线上一点,且CD=4,
(1)当AB=16时,求△ABC的面积;
(2)当AB变化时,求证:AD的值为定值,并求出这个定值.
【中考链接】
19、(2020?山东枣庄)
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为
?
A.10°
?B.15°
C.18°
D.30°
20、(2020?山东菏泽)
如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,求证:CE=DB.
参考答案
1、B
2、A
3、B
4、D
5、BD=BE或AD=CE或AB=BC等
6、AC=DE
7、①②③④
10、C
11、A
12、D
13、D
14、13
15、90
16、84
19、B
8、在△ABC中,高AD和BE交于F点,且AC
=BF,求:∠ABC的度数.
解:45°或135°
有2种情况,如图(1),(2)
?
∵∠BFD=∠AFE,
又AD和BE是△ABC的高,
∴∠ADC
=∠AEH
=90°,
∴∠DAC+∠C=90°,∠FAE+∠AFE=90°,
?
∴∠AFE=∠C,
∴∠C=∠BFD,
∵AC
=
BF,∠DAC
=∠FBD,∠BFD=∠C,?
∴△CAD
≌△
FBD,
?∴AD=BD.
?
如图(1)时∠ABC=45°;
?
如图(2)时∠ABC=135°.
?∵AD=BD,AD⊥BD,
?∴△ADB是等腰直角三角形,
?
∴∠ABD=45°,
?∴∠ABC=180°-45°=135°,?
故答案为:45°或135°.
9、如图,已知AD、AE,分别是两个钝角△ABC和△ABF的高,如果ADAE,ACAF.
?求证:BCBF.
证明:∵AD、AE,分别是两个钝角△ABC和△ABF的高,
∴∠D=∠E=90°,
在Rt△ADB和Rt△AEB中,
∵,
∴Rt△ADB≌Rt△AEB(HL),
∴
DB=EB,
在Rt△ADC和Rt△AEF中,
∵,
∴Rt△ADC≌Rt△AEF(HL),
∴
DC=EF,
∴BD-DC=EB-EF,
∴BCBF.
17、如图,在△ABC与△ADE中,AB=AC,AD=AE,连接BE、CD,若∠ABE=∠ACD=90°,
求证:OD=OE.
证明:证法(1):∵∠ABE=∠ADC=90°,
∴△ABE与△ACD均为直角三角形,
在Rt△ABE和Rt△ACD中,
∵,
∴Rt△ABE≌Rt△ACD(HL),
∴
BE=CD,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABE=∠ADC=90°,
∴∠CBE=∠BCD,
∴OB=OC,
∴OD=OE.
证法(2):∵∠ABE=∠ADC=90°,
∴△ABE与△ACD均为直角三角形,
在Rt△ABE和Rt△ACD中,
∵,
∴Rt△ABE≌Rt△ACD(HL),
∴∠AEB=∠ADC,
∵AD=AE,
∴∠ADE=∠AED,
∵∠ODE=∠OED,
∴OD=OE.
18、如图,在△ABC中,BC=12,AB=2AC,D为BC延长线上一点,且CD=4,
(1)当AB=16时,求△ABC的面积;
(2)当AB变化时,求证:AD的值为定值,并求出这个定值.
解:(1)如图(1),过C作CE⊥AB,垂足为点E,
设BE=x,则AE=16-x,
又BC=12,AB=16,AC=AB=8,
在Rt△BEC中,根据勾股定理得:x2+CE2=122①,
在Rt△AEC中,根据勾股定理得:(16-x)2+CE2=82②,
联立①②,消去CE2得:144-x2=64-(16-x)2,
解得:x=,
把x=代入①得:CE=,
则S△ABC=AB·CE=×12×=;
如图(2)
所示:,过A作AF⊥CD,垂足为点F,
设CF=x,AF=y,AC=a,AB=2a,
在Rt△ACF中,根据勾股定理得:x2+y2=a2①,
在Rt△ABF中,根据勾股定理得:(12+x)2+y2=(2a)2②,
②-①得:8x=
a2-48③,
在Rt△AFD中,根据勾股定理得:
AD2=AF2+FD2=y2+(4-x)2=x2+y2-8x+16,
将①和③代入得:AD2=a2+48-a2+16=64,
因为AD>0,
所以开方得:AD=8,
则AD的值为定值,且定值为8.
20、(2020?山东菏泽)
如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,求证:CE=DB.
证明:∵ED⊥AB,∴∠ADE=∠ACB=90°,∠A=∠A,
BC=DE,
?
∴△ABC≌△AED(AAS),?
∴AE=AB,AC=AD,?
∴CE=BD.
第18题图
第18题图(2)
第20题图
第15题图
第16题图
第5题图
第9题图
第20题图
第19题图
第14题图
第6题图
第7题图
第12题图
第2题图
第18题图
第13题图
第18题图(1)
第11题图
例题2图
第17题图
第17题图
第9题图
第8题图(1)
第8题图(2)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学下册第1章三角形的证明
1.2
直角三角形
第2课时
直角三角形2
【知识清单】
1、判定两个直角三角形全等的方法有HL、SSS、SAS、ASA、AAS
;
2、证明两个直角三角形全等的思路:首先考虑利用HL定理,再考虑利用一般的三角形全等的证明方法.
【经典例题】
例题1、已知:如图,∠ACB=∠ADB=90°,AC=AD,E在AB上.求证:CE=DE.
【考点】直角三角形全等的判定方法.
【分析】先利用HL判定Rt△ABC≌Rt△ABD,从而得到对应角相等,对应边相等,再利用SAS判定△BEC≌△BED,从而得到CE=DE.
【解答】证明:∵∠ACB=∠ADB=90°,
在Rt△ABC和Rt△ABD中,
AC=AD,AB=AB,
∴Rt△ABC≌Rt△ABD(HL).
∴∠ABC=∠ABD.
BC=BD.
在△BEC和△BED中,
BC=BD,∠ABC=∠ABD,BE=BE,
∴△BEC≌△BED(SAS),
∴CE=DE.
【点评】本题考查三角形全等的判定方法,判定两个直角三角形全等时,首先考虑HL定理,再考虑一般方法有:SSS、SAS、AAS.
例题2、(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.
【考点】?直角三角形全等的判定;全等三角形的性质.
【分析】根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AE=AD+DE,所以BD=DE+CE;
根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AD+AE=BD+CE,所以BD=DE-CE.
【解答】(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE-CE;
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵AB=AC,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE-CE.
【点评】此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS,SAS,
ASA,AAS等.这种类型的题目经常考到,要注意掌握.
【夯实基础】
1、已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和?△DEF全等
的是(??
?)?
A.AB=DE,AC=DF??????
???B.AC=EF,BC=DF?
C.AB=DE,BC=EF????????
??D.∠C=∠F,BC=EF
2、如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据
是(
)
A.HL
B.AAS
C.SSS
D.ASA
3、在直角三角形中,其中一个锐角是另一个锐角的3倍,则此三角形中最小的角是(
)
A.15°
B.22.5°
?C.30°?
D.45°
4、要判定两个直角三角形全等,下列说法正确的有(?
?)?
①有两条直角边对应相等;?②有两个锐角对应相等;?③有斜边和一条直角边对应相等;
?④有一条直角边和一个锐角相等;?⑤有斜边和一个锐角对应相等;??⑥有两条边相等.?
??A.6个
B.5个
C.4个
D.3个
5、如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE交于点F,请你添加
一个适当的条件:
,(答案不唯一),使△ADB≌△CEB.
6、如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要
添加的一个条件是
.
7、如图,在Rt△ABC中,AC⊥AB,垂足为A,AD⊥BC,垂足为D,∠1=∠2,有下列结
论:①AB∥DE;②∠B=∠3;③∠C=∠1;④∠B与∠2互余;⑤∠3=∠2.其中正确的
有
(填写正确的序号).
8、在△ABC中,高AD和BE交于F点,且AC
=BF,求:∠ABC的度数.
9、如图,已知AD、AE,分别是两个钝角△ABC和△ABF的高,如果ADAE,ACAF.
?
求证:BCBF.
【提优特训】
10、直角三角形两锐角的平分线所夹的钝角的度数为(
)
?A.100度
B.120度
C.135度
D.140度
11、如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AD=8,BD=6,则AC的长为
积为(
)
A.
B.
C.8
D.
12、如图,AB⊥AC,垂足为A,
DC⊥DB,垂足为D,AE⊥BC,DF⊥BC垂足分别为E、F,AB=DC,则图中全等三角形为(
)
A.
4对
B.
5对
C.
6对
D.
7对
13、如图,已知AB⊥DC,垂足为点P,若点P为DC的中点,AC=BD,则下列结论不成立的是
(
)
A.AC∥BD
B.AP=BP
C.∠A=∠B
D.AB=DC
14、如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的面积为
.
15、如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=________度
16、如图,在四边形ABCD中,∠B=∠D
=90°,∠BAD=135°,若AD=4cm,BC=10cm则四边形ABCD的面积为
cm?2.
17、如图,在△ABC与△ADE中,AB=AC,AD=AE,连接BE、CD,若∠ABE=∠ACD=90°,
求证:OD=OE.
18、如图,在△ABC中,BC=12,AB=2AC,D为BC延长线上一点,且CD=4,
(1)当AB=16时,求△ABC的面积;
(2)当AB变化时,求证:AD的值为定值,并求出这个定值.
【中考链接】
19、(2020?山东枣庄)
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为
?
A.10°
?B.15°
C.18°
D.30°
20、(2020?山东菏泽)
如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,求证:CE=DB.
参考答案
1、B
2、A
3、B
4、D
5、BD=BE或AD=CE或AB=BC等
6、AC=DE
7、①②③④
10、C
11、A
12、D
13、D
14、13
15、90
16、84
19、B
8、在△ABC中,高AD和BE交于F点,且AC
=BF,求:∠ABC的度数.
解:45°或135°
有2种情况,如图(1),(2)
?
∵∠BFD=∠AFE,
又AD和BE是△ABC的高,
∴∠ADC
=∠AEH
=90°,
∴∠DAC+∠C=90°,∠FAE+∠AFE=90°,
?
∴∠AFE=∠C,
∴∠C=∠BFD,
∵AC
=
BF,∠DAC
=∠FBD,∠BFD=∠C,?
∴△CAD
≌△
FBD,
?∴AD=BD.
?
如图(1)时∠ABC=45°;
?
如图(2)时∠ABC=135°.
?∵AD=BD,AD⊥BD,
?∴△ADB是等腰直角三角形,
?
∴∠ABD=45°,
?∴∠ABC=180°-45°=135°,?
故答案为:45°或135°.
9、如图,已知AD、AE,分别是两个钝角△ABC和△ABF的高,如果ADAE,ACAF.
?求证:BCBF.
证明:∵AD、AE,分别是两个钝角△ABC和△ABF的高,
∴∠D=∠E=90°,
在Rt△ADB和Rt△AEB中,
∵,
∴Rt△ADB≌Rt△AEB(HL),
∴
DB=EB,
在Rt△ADC和Rt△AEF中,
∵,
∴Rt△ADC≌Rt△AEF(HL),
∴
DC=EF,
∴BD-DC=EB-EF,
∴BCBF.
17、如图,在△ABC与△ADE中,AB=AC,AD=AE,连接BE、CD,若∠ABE=∠ACD=90°,
求证:OD=OE.
证明:证法(1):∵∠ABE=∠ADC=90°,
∴△ABE与△ACD均为直角三角形,
在Rt△ABE和Rt△ACD中,
∵,
∴Rt△ABE≌Rt△ACD(HL),
∴
BE=CD,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABE=∠ADC=90°,
∴∠CBE=∠BCD,
∴OB=OC,
∴OD=OE.
证法(2):∵∠ABE=∠ADC=90°,
∴△ABE与△ACD均为直角三角形,
在Rt△ABE和Rt△ACD中,
∵,
∴Rt△ABE≌Rt△ACD(HL),
∴∠AEB=∠ADC,
∵AD=AE,
∴∠ADE=∠AED,
∵∠ODE=∠OED,
∴OD=OE.
18、如图,在△ABC中,BC=12,AB=2AC,D为BC延长线上一点,且CD=4,
(1)当AB=16时,求△ABC的面积;
(2)当AB变化时,求证:AD的值为定值,并求出这个定值.
解:(1)如图(1),过C作CE⊥AB,垂足为点E,
设BE=x,则AE=16-x,
又BC=12,AB=16,AC=AB=8,
在Rt△BEC中,根据勾股定理得:x2+CE2=122①,
在Rt△AEC中,根据勾股定理得:(16-x)2+CE2=82②,
联立①②,消去CE2得:144-x2=64-(16-x)2,
解得:x=,
把x=代入①得:CE=,
则S△ABC=AB·CE=×12×=;
如图(2)
所示:,过A作AF⊥CD,垂足为点F,
设CF=x,AF=y,AC=a,AB=2a,
在Rt△ACF中,根据勾股定理得:x2+y2=a2①,
在Rt△ABF中,根据勾股定理得:(12+x)2+y2=(2a)2②,
②-①得:8x=
a2-48③,
在Rt△AFD中,根据勾股定理得:
AD2=AF2+FD2=y2+(4-x)2=x2+y2-8x+16,
将①和③代入得:AD2=a2+48-a2+16=64,
因为AD>0,
所以开方得:AD=8,
则AD的值为定值,且定值为8.
20、(2020?山东菏泽)
如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,求证:CE=DB.
证明:∵ED⊥AB,∴∠ADE=∠ACB=90°,∠A=∠A,
BC=DE,
?
∴△ABC≌△AED(AAS),?
∴AE=AB,AC=AD,?
∴CE=BD.
第18题图
第18题图(2)
第20题图
第15题图
第16题图
第5题图
第9题图
第20题图
第19题图
第14题图
第6题图
第7题图
第12题图
第2题图
第18题图
第13题图
第18题图(1)
第11题图
例题2图
第17题图
第17题图
第9题图
第8题图(1)
第8题图(2)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
