2020—2021学年人教版高一数学《二次方程实根分布》课件(共23张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《二次方程实根分布》课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 603.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览





文档简介
二次方程实根分布
设f(x)=ax2+bx+c (a>0), 则一元二次方程f(x)=0实根的分布情况可以由y=f(x)的图象或由韦达定理来确定.
定理:如果连续函数f(x)满足f(m) f(n)<0 (m<n),则方程f(x)=0在区间(m,n)内必有实数根.
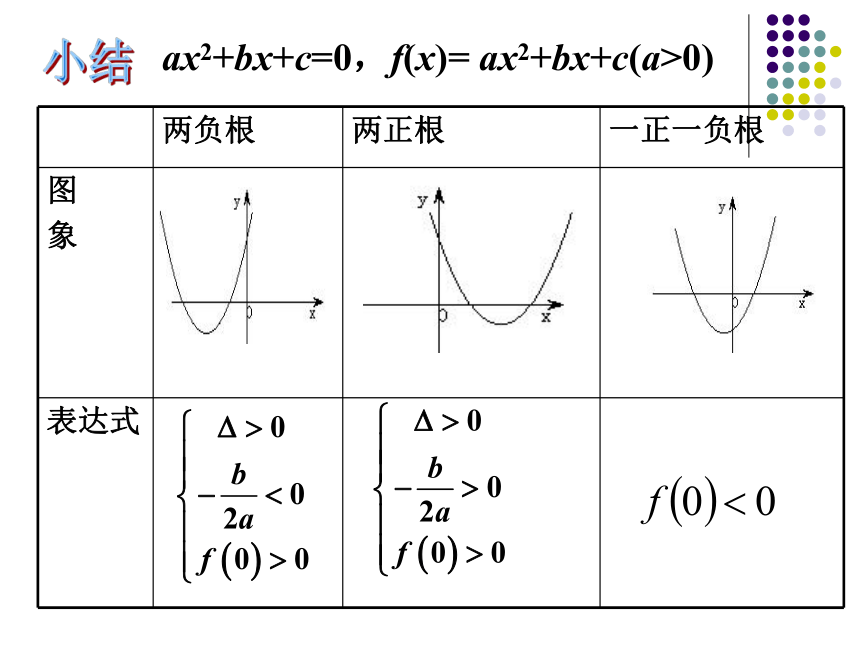
两负根
两正根
一正一负根
图
象
表达式
小结
ax2+bx+c=0,f(x)= ax2+bx+c(a>0)
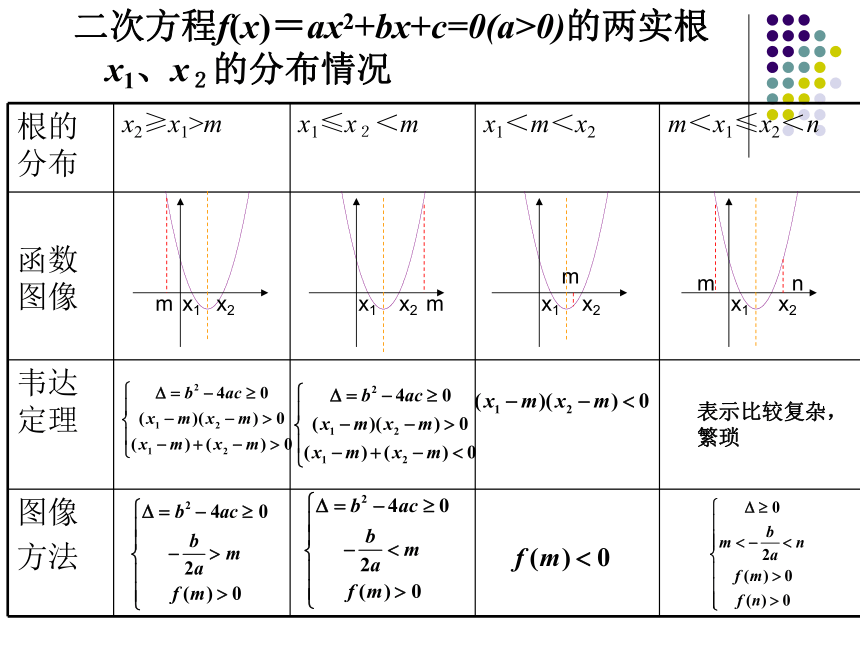
根的分布
x2≥x1>m
x1≤x2<m
x1<m<x2
m<x1≤x2<n
函数图像
韦达定理
图像
方法
m
x2
x1
x1
x2
m
x1
x2
m
x2
x1
n
m
表示比较复杂,繁琐
二次方程f(x)=ax2+bx+c=0(a>0)的两实根x1、x2的分布情况
例
(或△=0且-3<2m<0)
例
一元二次方程ax2+bx+c=0(a>0)(*) 有且仅有一个实根在区间(α,β)内的情形,
令f(x)= ax2+bx+c
2°若x=?是方程的一个实根;
1°若x=?且x=?都不是方程的一个实根;
若△=0,则对称轴在区间内即可;
若△>0,则
3°若x=?是方程的一个实根。
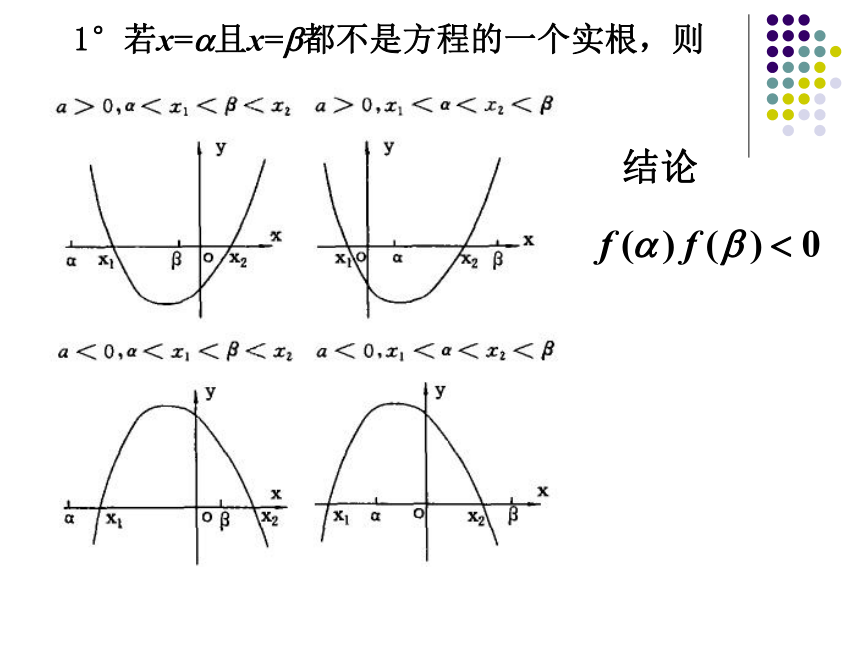
1°若x=?且x=?都不是方程的一个实根,则
结论
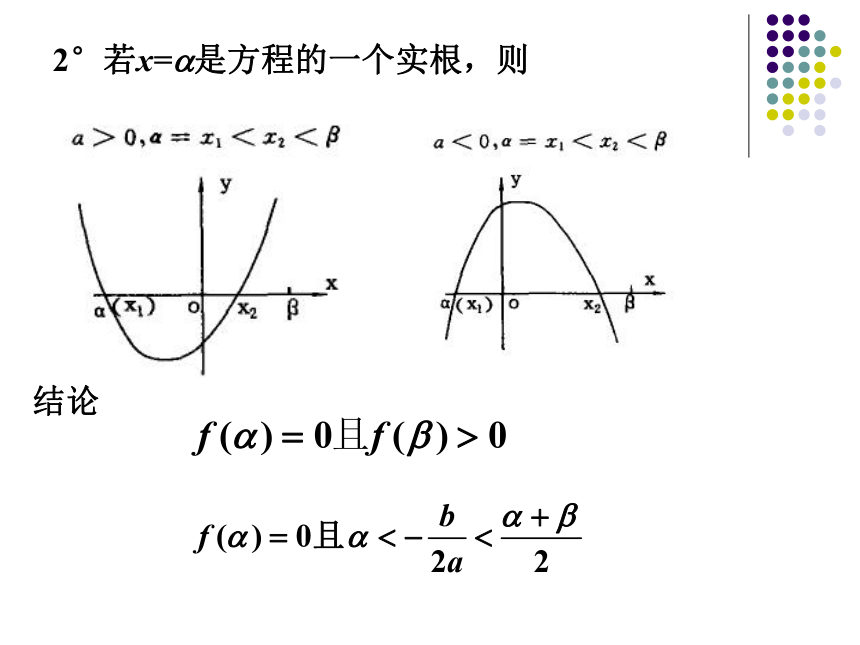
2°若x=?是方程的一个实根,则
结论
3°若x=?是方程的一个实根,则
结论
说明:事实上,这两种情形更多的是用求根检验法。
已知一元二次方程ax2+(2a-3)x+4=0(a≠0)有两个不等实根,且只有一个根在区间(0,1)上,求实数a的取值范围。
练习
已知a为实数,函数f(x)=2ax2+2x-3-a。
如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
已知a为实数,函数f(x)=2ax2+2x-3-a。如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
已知a为实数,函数f(x)=2ax2+2x-3-a。如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
已知a为实数,函数f(x)=2ax2+2x-3-a。如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
在下列条件下,分别求出m的取值范围
(1)方程x2-mx+4=0在[-1,1 ]有解;
练习2
从而有f(1)≤0或f(-1)≤0。
∵x1x2=4,∴ 在[-1,1]内有解,只能有一解,
解:设f(x)=x2-mx+4
设方程x2-mx+4=0的两根为x1,x2,
∴m的取值范围为m≤-5或m≥5。
在下列条件下,分别求出m的取值范围
(2)函数f(x)=x2-3x+4-m的图象与横轴 x在[-1,1 ]上有交点。
从而有f(1)≤0且f(-1)≥0。
∵x1+x2=3,∴ 在[-1,1]内有解,只能有一解,另一解大于1。
解:设f(x)=x2-3x+4-m
设方程x2-3x+4-m=0的两根为x1,x2,
∴m的取值范围为2≤m≤8。
练习2
所以0≤p≤1。
练习3
【解】线段AB的方程为2x-3y+5=0 (-1≤ x≤2), 将之代入曲线方程,
化简得22x2 + 20x+25-18a2=0.
令f (x) = 22x2 + 20x+25-18a2 (-1≤ x≤2),
则原题等价于抛物线在[-1,2]上与x轴无交点,
练习4
综上所述,实数a的取值范围是:
练习4
已知满足不等式 x2 -(a+1)x+a≤0的解在区间[1,3]内 , 求实数a取值范围。
解:
若a>1 , 则原不等式的解为 1≤x≤a ,
X
3
1
a
则 1 < a≤3
分析: 观察不难发现:a、1是 x2 -(a+1)x +a=0的根.
若a=1 , 则原不等式的解为 1,满足条件 ;
例4
已知满足不等式 x2 -(a+1)x+a≤0的解在区间[1,3]内 , 求实数a取值范围。
解:
若a<1 , 则原不等式的解为 a ≤ x≤ 1 ,
∴a取值范围是1≤a≤3
a
X
1
3
那么, 不可能满足题意。
例4
小结
一元二次方程实根分布总的来说是通过 数形结合来进行思考的,注意其思想方法的应用;
它的应用比较多,前面的例题都是它的一些典型应用,请同学们好好体会,并多加练习,才能很好的掌握。
设f(x)=ax2+bx+c (a>0), 则一元二次方程f(x)=0实根的分布情况可以由y=f(x)的图象或由韦达定理来确定.
定理:如果连续函数f(x)满足f(m) f(n)<0 (m<n),则方程f(x)=0在区间(m,n)内必有实数根.
两负根
两正根
一正一负根
图
象
表达式
小结
ax2+bx+c=0,f(x)= ax2+bx+c(a>0)
根的分布
x2≥x1>m
x1≤x2<m
x1<m<x2
m<x1≤x2<n
函数图像
韦达定理
图像
方法
m
x2
x1
x1
x2
m
x1
x2
m
x2
x1
n
m
表示比较复杂,繁琐
二次方程f(x)=ax2+bx+c=0(a>0)的两实根x1、x2的分布情况
例
(或△=0且-3<2m<0)
例
一元二次方程ax2+bx+c=0(a>0)(*) 有且仅有一个实根在区间(α,β)内的情形,
令f(x)= ax2+bx+c
2°若x=?是方程的一个实根;
1°若x=?且x=?都不是方程的一个实根;
若△=0,则对称轴在区间内即可;
若△>0,则
3°若x=?是方程的一个实根。
1°若x=?且x=?都不是方程的一个实根,则
结论
2°若x=?是方程的一个实根,则
结论
3°若x=?是方程的一个实根,则
结论
说明:事实上,这两种情形更多的是用求根检验法。
已知一元二次方程ax2+(2a-3)x+4=0(a≠0)有两个不等实根,且只有一个根在区间(0,1)上,求实数a的取值范围。
练习
已知a为实数,函数f(x)=2ax2+2x-3-a。
如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
已知a为实数,函数f(x)=2ax2+2x-3-a。如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
已知a为实数,函数f(x)=2ax2+2x-3-a。如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
已知a为实数,函数f(x)=2ax2+2x-3-a。如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。
例2
在下列条件下,分别求出m的取值范围
(1)方程x2-mx+4=0在[-1,1 ]有解;
练习2
从而有f(1)≤0或f(-1)≤0。
∵x1x2=4,∴ 在[-1,1]内有解,只能有一解,
解:设f(x)=x2-mx+4
设方程x2-mx+4=0的两根为x1,x2,
∴m的取值范围为m≤-5或m≥5。
在下列条件下,分别求出m的取值范围
(2)函数f(x)=x2-3x+4-m的图象与横轴 x在[-1,1 ]上有交点。
从而有f(1)≤0且f(-1)≥0。
∵x1+x2=3,∴ 在[-1,1]内有解,只能有一解,另一解大于1。
解:设f(x)=x2-3x+4-m
设方程x2-3x+4-m=0的两根为x1,x2,
∴m的取值范围为2≤m≤8。
练习2
所以0≤p≤1。
练习3
【解】线段AB的方程为2x-3y+5=0 (-1≤ x≤2), 将之代入曲线方程,
化简得22x2 + 20x+25-18a2=0.
令f (x) = 22x2 + 20x+25-18a2 (-1≤ x≤2),
则原题等价于抛物线在[-1,2]上与x轴无交点,
练习4
综上所述,实数a的取值范围是:
练习4
已知满足不等式 x2 -(a+1)x+a≤0的解在区间[1,3]内 , 求实数a取值范围。
解:
若a>1 , 则原不等式的解为 1≤x≤a ,
X
3
1
a
则 1 < a≤3
分析: 观察不难发现:a、1是 x2 -(a+1)x +a=0的根.
若a=1 , 则原不等式的解为 1,满足条件 ;
例4
已知满足不等式 x2 -(a+1)x+a≤0的解在区间[1,3]内 , 求实数a取值范围。
解:
若a<1 , 则原不等式的解为 a ≤ x≤ 1 ,
∴a取值范围是1≤a≤3
a
X
1
3
那么, 不可能满足题意。
例4
小结
一元二次方程实根分布总的来说是通过 数形结合来进行思考的,注意其思想方法的应用;
它的应用比较多,前面的例题都是它的一些典型应用,请同学们好好体会,并多加练习,才能很好的掌握。
