2020—2021学年人教版高一数学《2.3.4平面与平面垂直的性质》课件(28张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《2.3.4平面与平面垂直的性质》课件(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 772.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 20:45:09 | ||
图片预览




文档简介
2.3.4 平面与平面垂直的性质
复习两个平面垂直的定义,判定
什么是两个平面互相垂直?
两个平面相交,如果所成的二面角是直二面
角,就说这两个平面互相垂直.
如何判定两个平面互相垂直?
第一种方法根据定义,判定两个平面所成的二面角是直二面角;
第二种方法是根据判定定理,判定其中一个平面内有一条直线垂直于另一个平面.
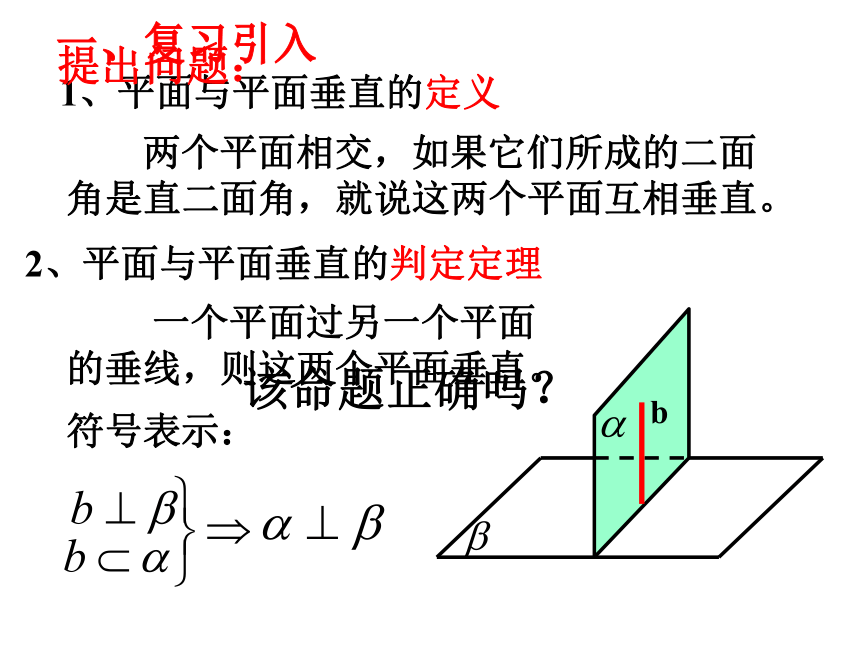
一、复习引入
1、平面与平面垂直的定义
2、平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
符号表示:
b
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
提出问题:
该命题正确吗?
1.黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
2.长方体ABCD-A1B1C1D1中,平面A1ADD1与平面ABCD垂直,平面A1ADD1内的直线A1A与平面ABCD垂直吗?
A
D
C
B
D1
A1
B1
C1
探索思考?
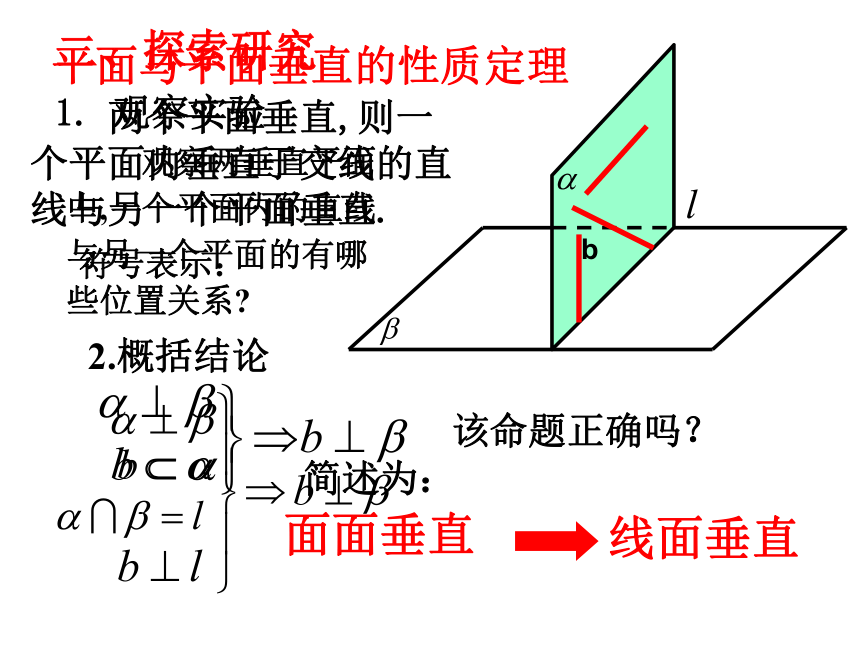
二、探索研究
1. 观察实验
观察两垂直平面中,一个平面内的直线与另一个平面的有哪些位置关系?
2.概括结论
平面与平面垂直的性质定理
b
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
简述为:
面面垂直
线面垂直
该命题正确吗?
符号表示:
b
C
A
D
E
B
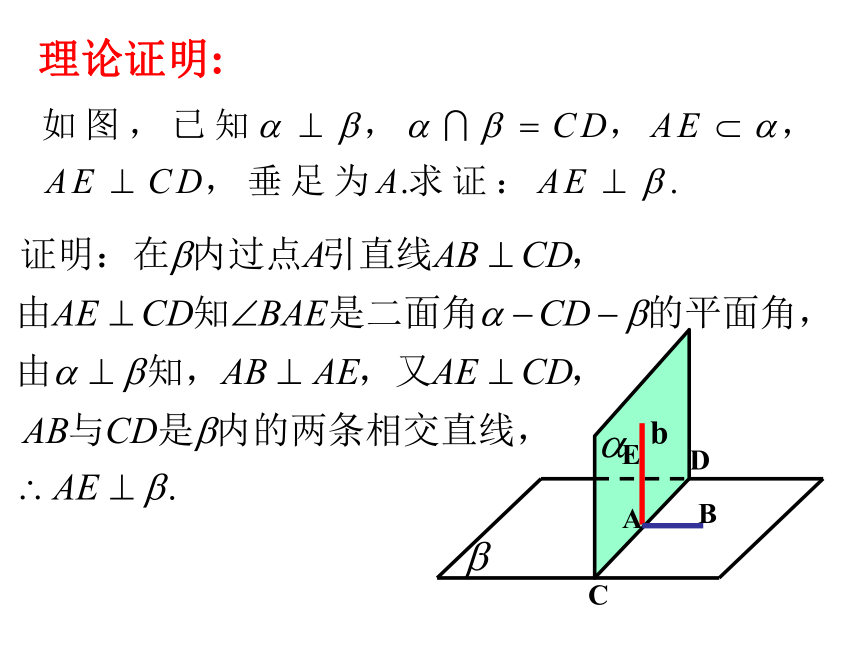
理论证明:
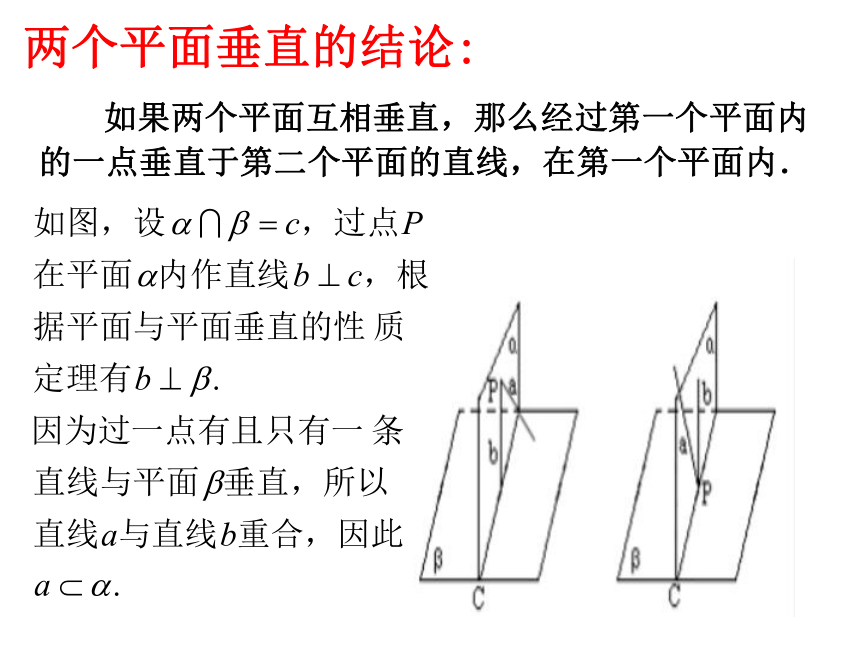
两个平面垂直的结论:
如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.
3.知识应用:
练习:判断正误.
已知平面α⊥平面β,α∩ β=l下列命题
(2)垂直于交线l的直线必垂直于平面β ( )
(3)过平面α内任意一点作交线的垂线,则此垂线必垂直于平面β( )
(1)平面α内的任意一条直线必垂直于平面β( )
√
×
×
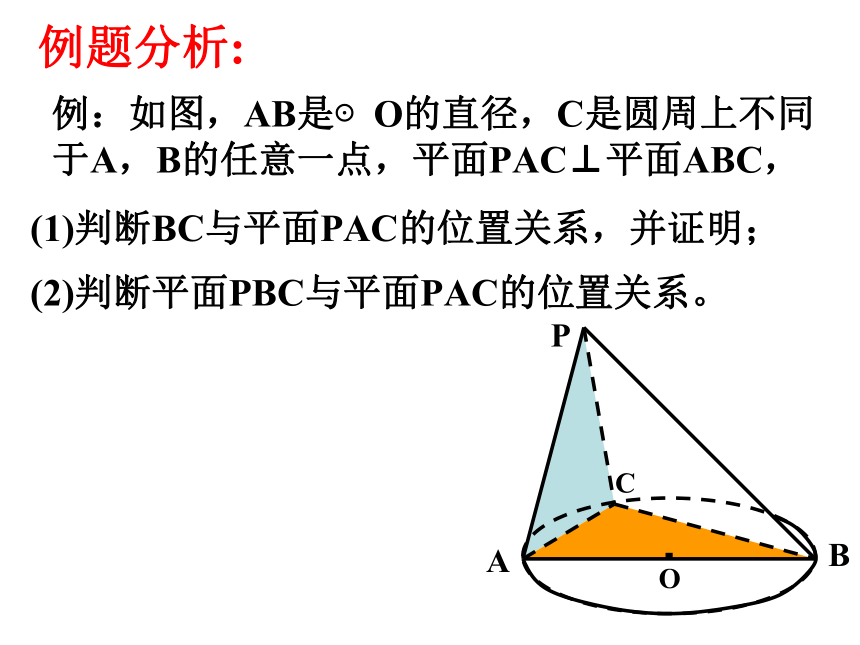
例:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
B
O
P
A
C
(2)判断平面PBC与平面PAC的位置关系。
(1)判断BC与平面PAC的位置关系,并证明;
例题分析:
(1)证明:∵ AB是⊙O的直径,
C是圆周上不同于A,B的任意一点
∴BC⊥平面PAC
(2) ∵ BC⊥平面PAC ,又BC 平面PBC ,
∴平面PBC⊥平面PAC
例:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
(1)判断BC与平面PAC的位置关系,并证明。
(2)判断平面PBC与平面PAC的位置关系。
∴∠ACB=90°即BC⊥AC
又∵平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
BC 平面ABC
B
O
P
A
C
2、本题充分地体现了面面垂直与 线面垂直之间的相互转化关系。
1、面面垂直的性质定理给我们提供了一种证明线面垂直的方法
面面垂直
线面垂直
性质定理
判定定理
解题反思:
a
b
c
1. 如图,已知平面 ,直线a满足
,试判断直线a与平面 的位置关系。
解:在 内作垂直于 与 交线的直线b,
因为 ,所以 .
因为 ,所以 .
又因为 ,所以 .
即直线a与平面 平行
巩固提升:
A
α
β
1、下列命题中错误的是( )
(A) 如果平面 ⊥平面 ,那么平面 内所有直线都垂直于平面
(B)如果平面 ⊥平面 ,那么平面 内一定存在直线平行于平面
(C)如果平面 不垂直于平面 ,则平面 内一定不存在直线垂直于平面
(D)如果平面 、 都垂直于平面 ,且 与 交于直线 a,则 a ⊥平面
α
β
α
β
β
β
β
α
α
α
β
β
α
α
知识巩固:
2、已知两个平面垂直,下列命题
①一个平面内已知直线必垂直于另一个平面内的任意直线;
②一个平面内的已知直线必垂直于另一个平面内的无数条直线;
③一个平面内的任意一条直线必垂直于另一个平面;
④过一个平面内的任意一点做交线的垂线,则此垂线必垂直于另一个平面。
其中正确命题的个数是( )
(A) 3 (B) 2 (C) 1 (D) 0
B
知识巩固:
例2.矩形ABCD中, AD=2,AB=1,现沿对角线AC折成直二面角D-AC-B,求折起后BD长度.
要点一 平面与平面垂直的性质的应用
在运用面面垂直性质定理时必须注意:(1)线在面内;(2)线垂直于两面的交线,由此才可以得出线面垂直.在应用线面平行、垂直的判定和性质定理证明有关问题时,在善于运用转化思想的同时,还应注意寻找线面平行、垂直所需的条件.
例1 如下图所示,P是四边形ABCD所在平面外的一点,
ABCD是∠DAB=60°且边长为a
的菱形.侧面PAD为正三角形,
其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
分析:①ABCD是边长为a的菱形;
②面PAD⊥面ABCD.
解答本题可先由面⊥面得线⊥面,再进一步得出线⊥线.
证明:(1)连接PG,由题知△PAD为正三角形,G是AD的中点,∴PG⊥AD.又平面PAD⊥平面ABCD,
∴PG⊥平面ABCD,∴PG⊥BG.
又∵四边形ABCD是菱形且∠DAB=60°,
∴△ABD是正三角形,∴BG⊥AD.
又AD∩PG=G,∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD,PG⊥AD.
所以AD⊥平面PBG,所以AD⊥PB.
规律方法:证明线面垂直,一种方法是利用线面垂直的判定定理,再一种方法是利用面面垂直的性质定理,本题已知面面垂直,故可考虑面面垂直的性质定理.
变式1 如图所示,α⊥β,CD?β,CD⊥AB,CE、EF?α,∠FEC=90°.
求证:面EFD⊥面DCE.
证明:∵α⊥β,CD?β,CD⊥AB,α∩β=AB,∴CD⊥α.
又∵EF?α,∴CD⊥EF.
又∠FEC=90°,∴EF⊥EC.
又EC∩CD=C,∴EF⊥面DCE.
又EF?面EFD,∴面EFD⊥面DCE.
例2 已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.
(1)求证:PA⊥平面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.
分析:由面面垂直向线面
垂直转化,一般要作一条
垂直于交线的直线,才能
应用性质定理.
证明:(1)在平面ABC内取一点D,作DF⊥AC于F,∵平面PAC⊥平面ABC,且交线为AC,∴DF⊥平面PAC.又∵PA?平面PAC,∴DF⊥PA.作DG⊥AB于G,同理可证DG⊥PA.
∵DG∩DF=D,∴PA⊥平面ABC.
(2)连接BE并延长交PC于H.
∵E是△PBC的垂心,∴PC⊥BH,
又AE⊥平面PBC,
故AE⊥PC,且AE∩BE=E,
∴PC⊥平面ABE.∴PC⊥AB.
又∵PA⊥平面ABC,∴PA⊥AB,
且PA∩PC=P,∴AB⊥平面PAC,
∴AB⊥AC,即△ABC是直角三角形.
规律方法:已知两个平面垂直时,过其中一个平面内的一点作交线的垂线,则由面面垂直的性质定理可得此直线垂直于另一个平面,于是面面垂直转化为线面垂直,由此得到结论:两个相交平面同时垂直于第三个平面,则它们的交线也垂直于第三个平面.证明(2)题的关键是要灵活利用(1)题的结论.
变式2 如图,已知平面α⊥平面γ,平面β⊥平面γ,α∩γ=a,β∩γ=b,且a∥b.求证:α∥β.
证明:如图,在平面α内作直线
PQ⊥a,在平面β内作直线MN⊥b,
垂足分别为Q、N.
∵α⊥γ,α∩γ=a,∴PQ⊥γ.
同理MN⊥γ.∴PQ∥MN.
∵PQ?β,MN?β,
∴PQ∥β.
同理a∥β.∵PQ?α,a?α,PQ∩a=Q,
∴α∥β.
要点二 线线、线面、面面垂直的综合应用
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化,每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
例3 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点.求证:
(1)EN∥平面PDC;
(2)BC⊥平面PEB;
(3)平面PBC⊥平面ADMN.
分析:(1)利用线面平行的判定定理证明,证EN∥DM.
(2)先证AD⊥平面PEB,再由AD∥BC证明.
(3)转化为证明PB⊥平面ADMN.
证明:(1)∵AD∥BC,BC?平面PBC,AD?平面PBC,∴AD∥平面PBC.
又平面ADMN∩平面PBC=MN,∴AD∥MN.
又∵BC∥AD,∴MN∥BC.
又N是PB的中点,∴点M为PC的中点.
(2)∵四边形ABCD是边长为2的菱形,且∠BAD=60°∴BE⊥AD.
又∵侧面PAD是正三角形,且E为中点,∴PE⊥AD,
∴AD⊥平面PBE.又∵AD∥BC,∴BC⊥平面PEB.
(3)由(2)知AD⊥平面PBE.又PB?平面PBE,∴AD⊥PB.
又∵PA=AB,N为PB的中点,∴AN⊥PB.且AN∩AD=A,
∴PB⊥平面ADMN.又∵PB?平面PBC.∴平面PBC⊥平面ADMN.
规律方法:运用平面垂直的性质定理时,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,这样把面面垂直转化为线面垂直或线线垂直.
变式3 如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
(1)求证:AD⊥PB;
(2)若E为BC边的中点,能否在棱上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
证明:(1)设G为AD的中点,
连接PG,∵△PAD为正三角形,∴PG⊥AD.
在菱形ABCD中,∠DAB=60°,
G为AD的中点,∴BG⊥AD.
又BG∩PG=G,∴AD⊥平面PGB.
∵PB?平面PGB,∴AD⊥PB.
(2)当F为PC的中点时,满足平面DEF⊥平面ABCD.取PC的中点F,连接DE、EF、DF,
在△PBC中,FE∥PB.在菱形ABCD中,GB∥DE,而FE?平面DEF,DE?平面DEF,EF∩DE=E.∴平面DEF∥平面PGB.
由(1)得PG⊥平面ABCD,而PG?平面PGB,
∴平面PGB⊥平面ABCD,
∴平面DEF⊥平面ABCD.
1、平面与平面垂直的性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
2、证明线面垂直的两种方法:
线线垂直→线面垂直;面面垂直→线面垂直
3、线线、线面、面面之间的平行与垂直关系的转化是解决空间图形问题的重要思想方法。
三、课堂小结:
复习两个平面垂直的定义,判定
什么是两个平面互相垂直?
两个平面相交,如果所成的二面角是直二面
角,就说这两个平面互相垂直.
如何判定两个平面互相垂直?
第一种方法根据定义,判定两个平面所成的二面角是直二面角;
第二种方法是根据判定定理,判定其中一个平面内有一条直线垂直于另一个平面.
一、复习引入
1、平面与平面垂直的定义
2、平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
符号表示:
b
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
提出问题:
该命题正确吗?
1.黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
2.长方体ABCD-A1B1C1D1中,平面A1ADD1与平面ABCD垂直,平面A1ADD1内的直线A1A与平面ABCD垂直吗?
A
D
C
B
D1
A1
B1
C1
探索思考?
二、探索研究
1. 观察实验
观察两垂直平面中,一个平面内的直线与另一个平面的有哪些位置关系?
2.概括结论
平面与平面垂直的性质定理
b
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
简述为:
面面垂直
线面垂直
该命题正确吗?
符号表示:
b
C
A
D
E
B
理论证明:
两个平面垂直的结论:
如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.
3.知识应用:
练习:判断正误.
已知平面α⊥平面β,α∩ β=l下列命题
(2)垂直于交线l的直线必垂直于平面β ( )
(3)过平面α内任意一点作交线的垂线,则此垂线必垂直于平面β( )
(1)平面α内的任意一条直线必垂直于平面β( )
√
×
×
例:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
B
O
P
A
C
(2)判断平面PBC与平面PAC的位置关系。
(1)判断BC与平面PAC的位置关系,并证明;
例题分析:
(1)证明:∵ AB是⊙O的直径,
C是圆周上不同于A,B的任意一点
∴BC⊥平面PAC
(2) ∵ BC⊥平面PAC ,又BC 平面PBC ,
∴平面PBC⊥平面PAC
例:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
(1)判断BC与平面PAC的位置关系,并证明。
(2)判断平面PBC与平面PAC的位置关系。
∴∠ACB=90°即BC⊥AC
又∵平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
BC 平面ABC
B
O
P
A
C
2、本题充分地体现了面面垂直与 线面垂直之间的相互转化关系。
1、面面垂直的性质定理给我们提供了一种证明线面垂直的方法
面面垂直
线面垂直
性质定理
判定定理
解题反思:
a
b
c
1. 如图,已知平面 ,直线a满足
,试判断直线a与平面 的位置关系。
解:在 内作垂直于 与 交线的直线b,
因为 ,所以 .
因为 ,所以 .
又因为 ,所以 .
即直线a与平面 平行
巩固提升:
A
α
β
1、下列命题中错误的是( )
(A) 如果平面 ⊥平面 ,那么平面 内所有直线都垂直于平面
(B)如果平面 ⊥平面 ,那么平面 内一定存在直线平行于平面
(C)如果平面 不垂直于平面 ,则平面 内一定不存在直线垂直于平面
(D)如果平面 、 都垂直于平面 ,且 与 交于直线 a,则 a ⊥平面
α
β
α
β
β
β
β
α
α
α
β
β
α
α
知识巩固:
2、已知两个平面垂直,下列命题
①一个平面内已知直线必垂直于另一个平面内的任意直线;
②一个平面内的已知直线必垂直于另一个平面内的无数条直线;
③一个平面内的任意一条直线必垂直于另一个平面;
④过一个平面内的任意一点做交线的垂线,则此垂线必垂直于另一个平面。
其中正确命题的个数是( )
(A) 3 (B) 2 (C) 1 (D) 0
B
知识巩固:
例2.矩形ABCD中, AD=2,AB=1,现沿对角线AC折成直二面角D-AC-B,求折起后BD长度.
要点一 平面与平面垂直的性质的应用
在运用面面垂直性质定理时必须注意:(1)线在面内;(2)线垂直于两面的交线,由此才可以得出线面垂直.在应用线面平行、垂直的判定和性质定理证明有关问题时,在善于运用转化思想的同时,还应注意寻找线面平行、垂直所需的条件.
例1 如下图所示,P是四边形ABCD所在平面外的一点,
ABCD是∠DAB=60°且边长为a
的菱形.侧面PAD为正三角形,
其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
分析:①ABCD是边长为a的菱形;
②面PAD⊥面ABCD.
解答本题可先由面⊥面得线⊥面,再进一步得出线⊥线.
证明:(1)连接PG,由题知△PAD为正三角形,G是AD的中点,∴PG⊥AD.又平面PAD⊥平面ABCD,
∴PG⊥平面ABCD,∴PG⊥BG.
又∵四边形ABCD是菱形且∠DAB=60°,
∴△ABD是正三角形,∴BG⊥AD.
又AD∩PG=G,∴BG⊥平面PAD.
(2)由(1)可知BG⊥AD,PG⊥AD.
所以AD⊥平面PBG,所以AD⊥PB.
规律方法:证明线面垂直,一种方法是利用线面垂直的判定定理,再一种方法是利用面面垂直的性质定理,本题已知面面垂直,故可考虑面面垂直的性质定理.
变式1 如图所示,α⊥β,CD?β,CD⊥AB,CE、EF?α,∠FEC=90°.
求证:面EFD⊥面DCE.
证明:∵α⊥β,CD?β,CD⊥AB,α∩β=AB,∴CD⊥α.
又∵EF?α,∴CD⊥EF.
又∠FEC=90°,∴EF⊥EC.
又EC∩CD=C,∴EF⊥面DCE.
又EF?面EFD,∴面EFD⊥面DCE.
例2 已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.
(1)求证:PA⊥平面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.
分析:由面面垂直向线面
垂直转化,一般要作一条
垂直于交线的直线,才能
应用性质定理.
证明:(1)在平面ABC内取一点D,作DF⊥AC于F,∵平面PAC⊥平面ABC,且交线为AC,∴DF⊥平面PAC.又∵PA?平面PAC,∴DF⊥PA.作DG⊥AB于G,同理可证DG⊥PA.
∵DG∩DF=D,∴PA⊥平面ABC.
(2)连接BE并延长交PC于H.
∵E是△PBC的垂心,∴PC⊥BH,
又AE⊥平面PBC,
故AE⊥PC,且AE∩BE=E,
∴PC⊥平面ABE.∴PC⊥AB.
又∵PA⊥平面ABC,∴PA⊥AB,
且PA∩PC=P,∴AB⊥平面PAC,
∴AB⊥AC,即△ABC是直角三角形.
规律方法:已知两个平面垂直时,过其中一个平面内的一点作交线的垂线,则由面面垂直的性质定理可得此直线垂直于另一个平面,于是面面垂直转化为线面垂直,由此得到结论:两个相交平面同时垂直于第三个平面,则它们的交线也垂直于第三个平面.证明(2)题的关键是要灵活利用(1)题的结论.
变式2 如图,已知平面α⊥平面γ,平面β⊥平面γ,α∩γ=a,β∩γ=b,且a∥b.求证:α∥β.
证明:如图,在平面α内作直线
PQ⊥a,在平面β内作直线MN⊥b,
垂足分别为Q、N.
∵α⊥γ,α∩γ=a,∴PQ⊥γ.
同理MN⊥γ.∴PQ∥MN.
∵PQ?β,MN?β,
∴PQ∥β.
同理a∥β.∵PQ?α,a?α,PQ∩a=Q,
∴α∥β.
要点二 线线、线面、面面垂直的综合应用
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化,每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
例3 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点.求证:
(1)EN∥平面PDC;
(2)BC⊥平面PEB;
(3)平面PBC⊥平面ADMN.
分析:(1)利用线面平行的判定定理证明,证EN∥DM.
(2)先证AD⊥平面PEB,再由AD∥BC证明.
(3)转化为证明PB⊥平面ADMN.
证明:(1)∵AD∥BC,BC?平面PBC,AD?平面PBC,∴AD∥平面PBC.
又平面ADMN∩平面PBC=MN,∴AD∥MN.
又∵BC∥AD,∴MN∥BC.
又N是PB的中点,∴点M为PC的中点.
(2)∵四边形ABCD是边长为2的菱形,且∠BAD=60°∴BE⊥AD.
又∵侧面PAD是正三角形,且E为中点,∴PE⊥AD,
∴AD⊥平面PBE.又∵AD∥BC,∴BC⊥平面PEB.
(3)由(2)知AD⊥平面PBE.又PB?平面PBE,∴AD⊥PB.
又∵PA=AB,N为PB的中点,∴AN⊥PB.且AN∩AD=A,
∴PB⊥平面ADMN.又∵PB?平面PBC.∴平面PBC⊥平面ADMN.
规律方法:运用平面垂直的性质定理时,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,这样把面面垂直转化为线面垂直或线线垂直.
变式3 如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
(1)求证:AD⊥PB;
(2)若E为BC边的中点,能否在棱上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
证明:(1)设G为AD的中点,
连接PG,∵△PAD为正三角形,∴PG⊥AD.
在菱形ABCD中,∠DAB=60°,
G为AD的中点,∴BG⊥AD.
又BG∩PG=G,∴AD⊥平面PGB.
∵PB?平面PGB,∴AD⊥PB.
(2)当F为PC的中点时,满足平面DEF⊥平面ABCD.取PC的中点F,连接DE、EF、DF,
在△PBC中,FE∥PB.在菱形ABCD中,GB∥DE,而FE?平面DEF,DE?平面DEF,EF∩DE=E.∴平面DEF∥平面PGB.
由(1)得PG⊥平面ABCD,而PG?平面PGB,
∴平面PGB⊥平面ABCD,
∴平面DEF⊥平面ABCD.
1、平面与平面垂直的性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
2、证明线面垂直的两种方法:
线线垂直→线面垂直;面面垂直→线面垂直
3、线线、线面、面面之间的平行与垂直关系的转化是解决空间图形问题的重要思想方法。
三、课堂小结:
