2020—2021学年人教版高一数学《2.2平面与平面平行的性质》课件(22张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《2.2平面与平面平行的性质》课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 275.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 21:07:32 | ||
图片预览





文档简介
平面与平面
垂直的性质
问题提出
1.平面与平面垂直的定义是什么?如何判定平面与平面垂直?
2.平面与平面垂直的判定定理,解决了两个平面垂直的条件问题;反之,在平面与平面垂直的条件下,能得到哪些结论?
定义和判定定理
知识探究(一)平面与平面垂直的性质定理
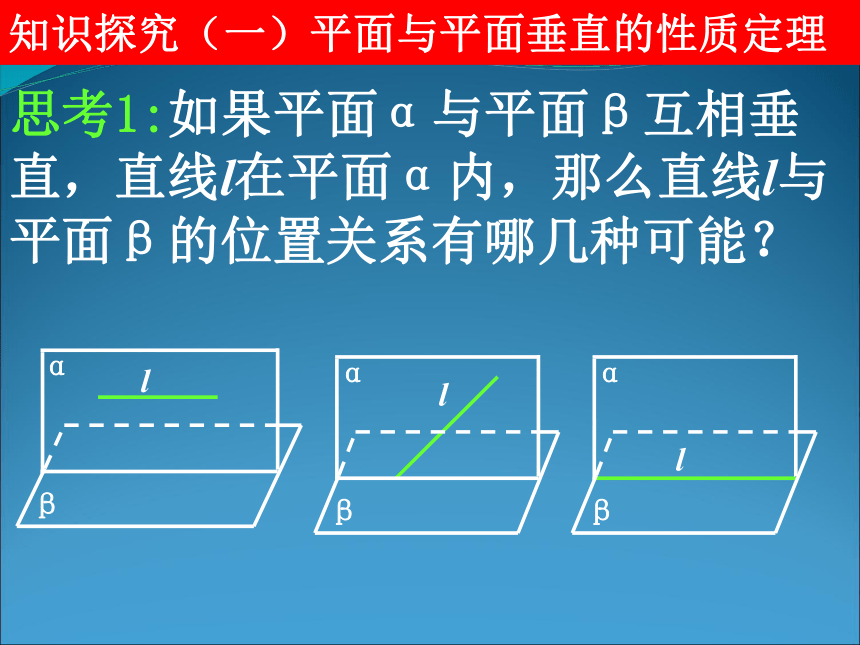
思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
α
β
l
l
α
β
l
α
β
知识探究(一)平面与平面垂直的性质定理
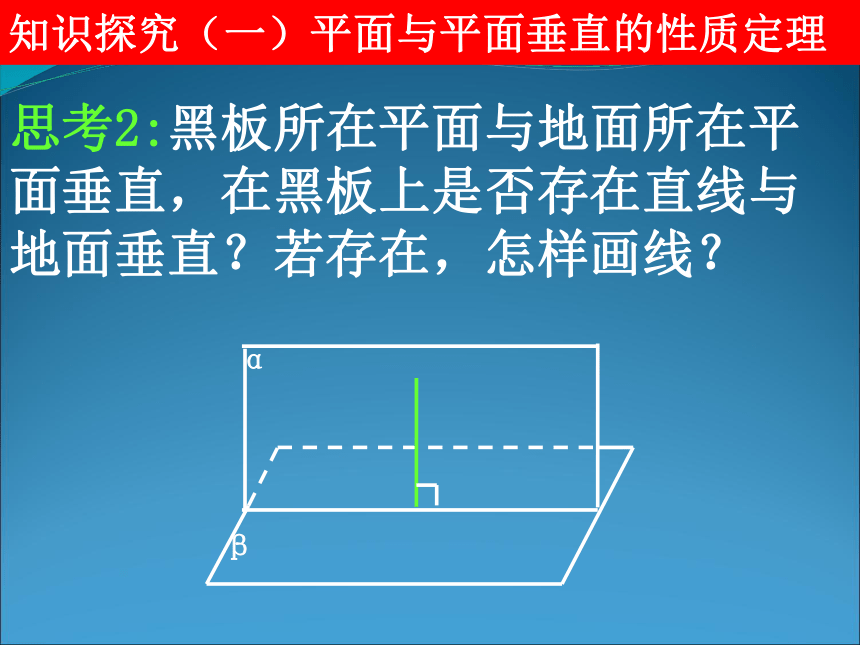
思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?
α
β
思考3:如图,长方体ABCD—A1B1C1D1中,平面A1ADD1与平面ABCD垂直,其交线为AD,直线A1A,D1D都在平面A1ADD1内,且都与交线AD垂直,这两条直线与平面ABCD垂直吗?
A
A1
B
C
D
B1
C1
D1
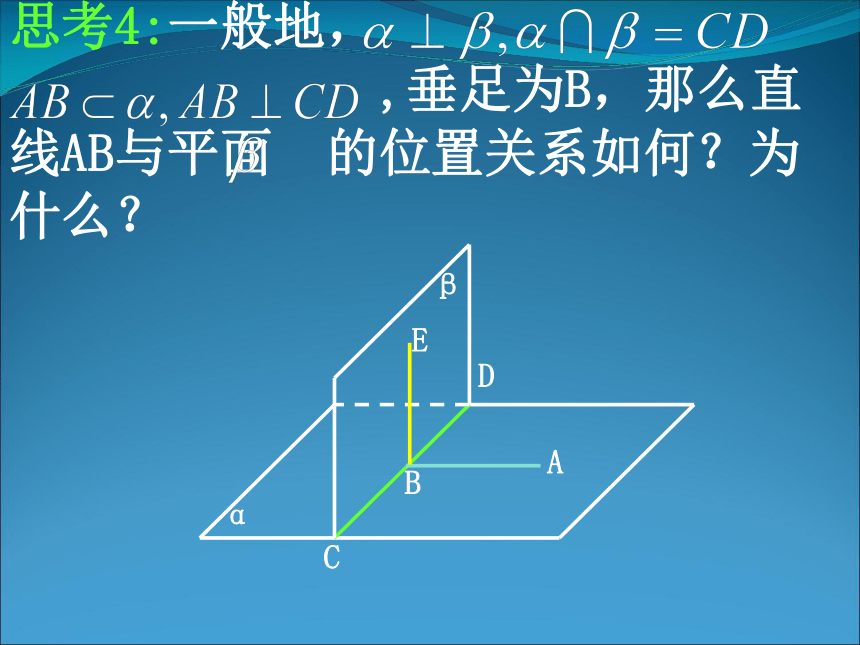
思考4:一般地,
,垂足为B,那么直线AB与平面 的位置关系如何?为什么?
α
β
A
B
D
C
E
思考5:据上分析可得什么定理?试用文字语言表述之.
定理 两个平面垂直,则在一个平面内垂直交线的直线与另一个平面垂直.
α
β
A
B
D
C
思考6:上述定理通常叫做两平面垂直的性质定理,结合下图,如何用符号语言描述这个定理?
α
β
l
m
知识探究(二)平面与平面垂直的性质探究
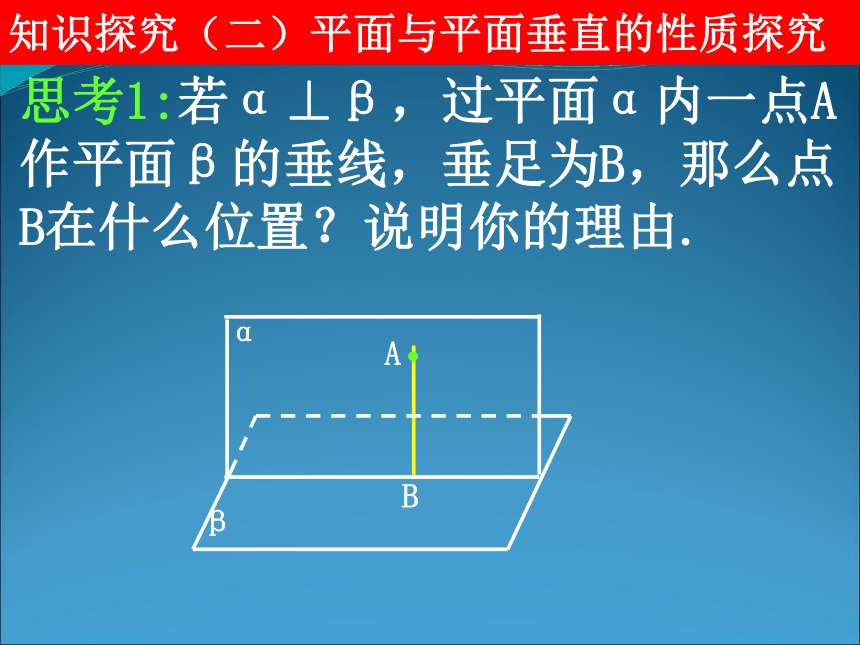
思考1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.
B
α
β
A
思考2:上述分析表明:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.
B
α
β
A
思考3:对于三个平面α、β、γ,如果α⊥γ,β⊥γ, ,那么直线l与平面γ的位置关系如何?为什么?
α
β
γ
l
a
b
思考4:上述结论如何用文字语言表述?
如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
α
β
γ
l
理论迁移
如图,已知α⊥β,l⊥β,
,试判断直线l与平面α的位置关系,并说明理由.
α
β
l
m
a
1.定理 两个平面垂直,则在一个平面内垂直交线的直线与另一个平面垂直.
2.如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.
3.如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
α
β
A
B
D
C
B
α
β
A
α
β
γ
l
α
β
l
m
a
4.如果一条直线与一个平面都与第三个平面垂直,则这条直线在这个平面内或与平面平行。
两个平面垂直应用举例
例题1? 如图4,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在平面,D、E分别是VA、VC的中点,直线 DE与平面VBC有什么关系?试说明理由.
解:由VC垂直于⊙O所在平面,知VC⊥AC,VC⊥BC,即 ∠ACB是二面角A-VC-B的平面角.由∠ACB是直径上的圆周角,知 ∠ACB =90°。
因此,平面 VAC⊥平面VBC.由DE是△VAC两边中点连线,知 DE∥AC,故DE⊥VC.由两个平面垂直的性质定理,知直线DE与平面VBC垂直。
注意:本题也可以先推出AC垂直于平面VBC,再由DE∥AC,推出上面的结论。
例2.S为三角形ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC。 求证:AB⊥BC。
S
C
B
A
证明:过A点作AD⊥SB于D点.
∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC,
∴ AD⊥BC.
又∵ SA ⊥ 平面ABC, ∴SA ⊥ BC. AD∩SA=A
∴BC ⊥ 平面SAB.
∴BC ⊥AB.
D
例3如图,四棱锥P-ABCD的底面是矩形,AB=2, ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角.
P
A
B
C
D
E
[总结提炼]
☆ 已知面面垂直易找面的垂线,且在某一个平面内
☆ 解题过程中应注意充分领悟、应用
☆ 证明面面垂直要从寻找面的垂线入手
☆ 理解面面垂直的判定与性质都要依赖面面垂直的定义
☆ 定义面面垂直是在建立在二面角的定义的基础上的
线面垂直
面面垂直
线线垂直
面面垂直
线面垂直
线线垂直
α
β
a
A
B
线线垂直
线面垂直
线线平行
面面平行
面面垂直
垂直、平行关系小结
2.面面垂直的性质推论:
1.平面与平面垂直的性质定理:
面面垂直
线面垂直
α
β
γ
l
α
β
A
b
a
l
β
α
P
a
a∥α
D
C
A
B
作业:习题1、2、3
1414班,我们是最棒的!
see you later!
垂直的性质
问题提出
1.平面与平面垂直的定义是什么?如何判定平面与平面垂直?
2.平面与平面垂直的判定定理,解决了两个平面垂直的条件问题;反之,在平面与平面垂直的条件下,能得到哪些结论?
定义和判定定理
知识探究(一)平面与平面垂直的性质定理
思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
α
β
l
l
α
β
l
α
β
知识探究(一)平面与平面垂直的性质定理
思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?
α
β
思考3:如图,长方体ABCD—A1B1C1D1中,平面A1ADD1与平面ABCD垂直,其交线为AD,直线A1A,D1D都在平面A1ADD1内,且都与交线AD垂直,这两条直线与平面ABCD垂直吗?
A
A1
B
C
D
B1
C1
D1
思考4:一般地,
,垂足为B,那么直线AB与平面 的位置关系如何?为什么?
α
β
A
B
D
C
E
思考5:据上分析可得什么定理?试用文字语言表述之.
定理 两个平面垂直,则在一个平面内垂直交线的直线与另一个平面垂直.
α
β
A
B
D
C
思考6:上述定理通常叫做两平面垂直的性质定理,结合下图,如何用符号语言描述这个定理?
α
β
l
m
知识探究(二)平面与平面垂直的性质探究
思考1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.
B
α
β
A
思考2:上述分析表明:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.
B
α
β
A
思考3:对于三个平面α、β、γ,如果α⊥γ,β⊥γ, ,那么直线l与平面γ的位置关系如何?为什么?
α
β
γ
l
a
b
思考4:上述结论如何用文字语言表述?
如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
α
β
γ
l
理论迁移
如图,已知α⊥β,l⊥β,
,试判断直线l与平面α的位置关系,并说明理由.
α
β
l
m
a
1.定理 两个平面垂直,则在一个平面内垂直交线的直线与另一个平面垂直.
2.如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.
3.如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
α
β
A
B
D
C
B
α
β
A
α
β
γ
l
α
β
l
m
a
4.如果一条直线与一个平面都与第三个平面垂直,则这条直线在这个平面内或与平面平行。
两个平面垂直应用举例
例题1? 如图4,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在平面,D、E分别是VA、VC的中点,直线 DE与平面VBC有什么关系?试说明理由.
解:由VC垂直于⊙O所在平面,知VC⊥AC,VC⊥BC,即 ∠ACB是二面角A-VC-B的平面角.由∠ACB是直径上的圆周角,知 ∠ACB =90°。
因此,平面 VAC⊥平面VBC.由DE是△VAC两边中点连线,知 DE∥AC,故DE⊥VC.由两个平面垂直的性质定理,知直线DE与平面VBC垂直。
注意:本题也可以先推出AC垂直于平面VBC,再由DE∥AC,推出上面的结论。
例2.S为三角形ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC。 求证:AB⊥BC。
S
C
B
A
证明:过A点作AD⊥SB于D点.
∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC,
∴ AD⊥BC.
又∵ SA ⊥ 平面ABC, ∴SA ⊥ BC. AD∩SA=A
∴BC ⊥ 平面SAB.
∴BC ⊥AB.
D
例3如图,四棱锥P-ABCD的底面是矩形,AB=2, ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角.
P
A
B
C
D
E
[总结提炼]
☆ 已知面面垂直易找面的垂线,且在某一个平面内
☆ 解题过程中应注意充分领悟、应用
☆ 证明面面垂直要从寻找面的垂线入手
☆ 理解面面垂直的判定与性质都要依赖面面垂直的定义
☆ 定义面面垂直是在建立在二面角的定义的基础上的
线面垂直
面面垂直
线线垂直
面面垂直
线面垂直
线线垂直
α
β
a
A
B
线线垂直
线面垂直
线线平行
面面平行
面面垂直
垂直、平行关系小结
2.面面垂直的性质推论:
1.平面与平面垂直的性质定理:
面面垂直
线面垂直
α
β
γ
l
α
β
A
b
a
l
β
α
P
a
a∥α
D
C
A
B
作业:习题1、2、3
1414班,我们是最棒的!
see you later!
