2020—2021学年人教版高一数学《2.3.1直线与平面垂直的判定》课件(27张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《2.3.1直线与平面垂直的判定》课件(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览







文档简介
第二章 点、线、面之间的位置关系
2.3.1直线与平面垂直的概念与判定
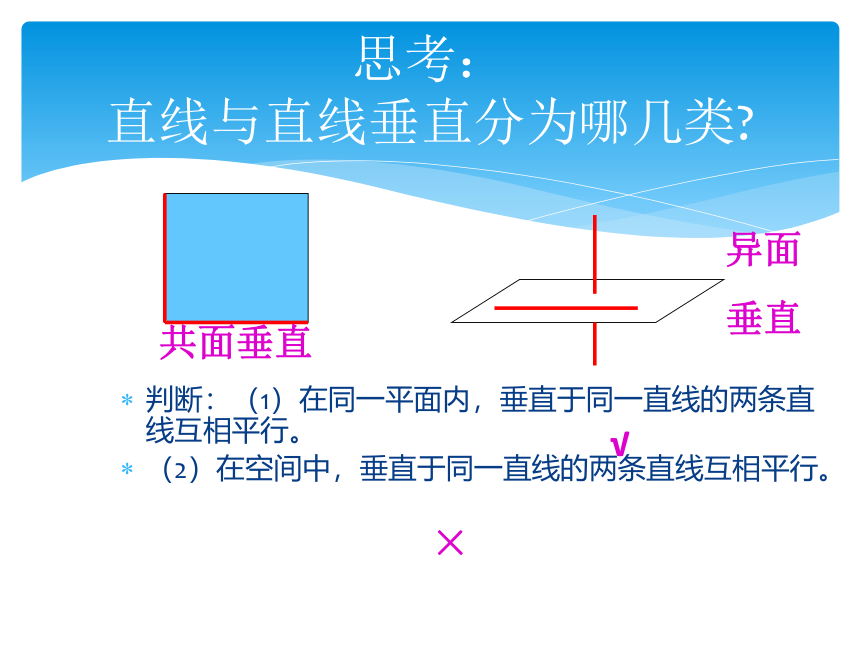
思考:
直线与直线垂直分为哪几类?
判断:(1)在同一平面内,垂直于同一直线的两条直线互相平行。
(2)在空间中,垂直于同一直线的两条直线互相平行。
共面垂直
异面
垂直
√
×
问题探究(一):直线与平面垂直的概念
思考:操场地面上竖立的旗杆与地面的位置关系给人以什么感觉?你还能列举一些类似的实例吗?
l
?
o
D
C
B
A
m
E
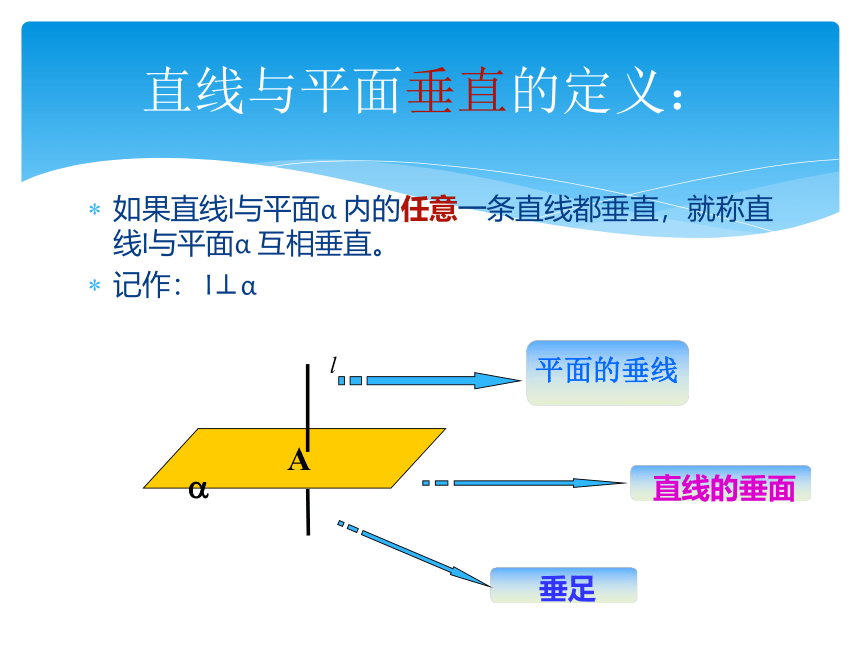
直线与平面垂直的定义:
如果直线l与平面α 内的任意一条直线都垂直,就称直线l与平面α 互相垂直。
记作: l⊥α
平面的垂线
?
A
直线的垂面
垂足
思考:如果一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直吗?
问题探究(二):直线与平面垂直的判定
思考:对于一条直线和一个平面,如果根据定义来判断它们是否垂直,需要解决什么问题?如何操作?
思考:我们需要寻求一个简单可行的办法来判定直线与平面垂直.
如果直线l与平面α内的两条直线垂直,能保证l⊥α吗?
如果直线l与平面α内的一条直线垂直,能保证l⊥α吗?
思考:如图,将一块三角形纸片ABC沿折痕AD折起,把翻折后的纸片竖起放置在桌面上,使BD、DC与桌面接触,观察折痕AD与桌面的位置关系.
A
B
C
D
A
B
C
D
思考:由上可知当折痕AD垂直平面α内的两条相交直线时,折痕AD与平面α垂直.由此我们是否能得出直线与平面垂直的判定方法?
A
B
C
D
A
B
C
D
如何调整折痕AD的位置,才能使翻折后直线AD与桌面所在的平面垂直?
定理: 如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
思考:上述定理通常称为直线和平面垂直的判定定理,它是判定直线与平面垂直的理论依据.结合下图,怎样用符号语言表述这个定理?
α
a
l
P
b
例题讲解
例1 已知 .求证:
α
a
b
c
d
例2 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,求证:
(1)AD⊥BC (2)PC ⊥AD
P
A
B
C
D
P66 探究:
如图,直四棱柱A’B’C’D’-ABCD中,底面四边形ABCD满足什么条件时,A’C⊥B’D’?
1、如图,在正方体ABCD-A1B1C1D1中,
(1)请列举与平面ABCD垂直的直线 ;
(2)你还能找出一条与平面D1DBB1垂直的直线吗?
A
B
C
D
A1
B1
C1
D1
课堂检测
思考:你还能找出一条与平面A1C1B垂直的直线吗?
思考:直线与平面有哪些位置关系?
α
a
A
垂直
斜交
问题探究(三):平面的斜线
思考:当直线与平面相交时,它们可能垂直,也可能不垂直,如果一条直线和一个平面相交但不垂直,这条直线叫做这个平面的斜线,斜线和平面的交点叫做斜足.那么过一点作一个平面的斜线有多少条?
α
l
P
斜线
斜足
思考:过斜线上斜足外一点向平面引垂线,连结垂足和斜足的直线叫做这条斜线在这个平面上的射影.那么斜线l在平面α内的射影有几条?
α
l
P
A
B
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
O
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
E
巩固练习
思考:如图,过平面α外一点P引平面α的两条斜线段PA、PB,斜足为A、B,再过点P引平面α的垂线,垂足为O,如果PA>PB,那么OA与OB的大小关系如何?反之成立吗?
α
O
P
A
B
思考:如图,直线l是平面α的一条斜线,它在平面α内的射影为b,直线a在平面α内,如果a⊥b,那么直线a与直线l垂直吗?为什么?反之成立吗?
a
α
l
b
思考:我们把平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角.在实际应用或解题中,怎样去求这个角?
α
P
A
B
线面所成的角:
(1)斜线与平面所成的角:
规定:平面一条斜线与它在平面上的射影所成的锐角,称为这条直线与这个平面所成的角。
范围:
(2)垂线与平面所成的角为:
(3)规定:当l∥α 或l在α 内时,
l与α 所成的角为:
(0°,90°)
90°
0°
α
A
P
O
例题讲解
例3 在正方体ABCD-A1B1C1D1中.
(1)求直线A1B和平面ABCD所成的角;
(2)求直线A1B和平面A1B1CD所成的角.
D1
A
B
A1
C
B1
C1
D
O
归纳小结
1.直线与平面垂直的概念
(1)利用定义;
(2)利用判定定理.
3.数学思想方法:转化的思想
空间问题
平面问题
3.直线与平面垂直的判定
线线垂直
线面垂直
垂直于平面内任意一条直线
2. 线面角的概念及范围
2.3.1直线与平面垂直的概念与判定
思考:
直线与直线垂直分为哪几类?
判断:(1)在同一平面内,垂直于同一直线的两条直线互相平行。
(2)在空间中,垂直于同一直线的两条直线互相平行。
共面垂直
异面
垂直
√
×
问题探究(一):直线与平面垂直的概念
思考:操场地面上竖立的旗杆与地面的位置关系给人以什么感觉?你还能列举一些类似的实例吗?
l
?
o
D
C
B
A
m
E
直线与平面垂直的定义:
如果直线l与平面α 内的任意一条直线都垂直,就称直线l与平面α 互相垂直。
记作: l⊥α
平面的垂线
?
A
直线的垂面
垂足
思考:如果一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直吗?
问题探究(二):直线与平面垂直的判定
思考:对于一条直线和一个平面,如果根据定义来判断它们是否垂直,需要解决什么问题?如何操作?
思考:我们需要寻求一个简单可行的办法来判定直线与平面垂直.
如果直线l与平面α内的两条直线垂直,能保证l⊥α吗?
如果直线l与平面α内的一条直线垂直,能保证l⊥α吗?
思考:如图,将一块三角形纸片ABC沿折痕AD折起,把翻折后的纸片竖起放置在桌面上,使BD、DC与桌面接触,观察折痕AD与桌面的位置关系.
A
B
C
D
A
B
C
D
思考:由上可知当折痕AD垂直平面α内的两条相交直线时,折痕AD与平面α垂直.由此我们是否能得出直线与平面垂直的判定方法?
A
B
C
D
A
B
C
D
如何调整折痕AD的位置,才能使翻折后直线AD与桌面所在的平面垂直?
定理: 如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
思考:上述定理通常称为直线和平面垂直的判定定理,它是判定直线与平面垂直的理论依据.结合下图,怎样用符号语言表述这个定理?
α
a
l
P
b
例题讲解
例1 已知 .求证:
α
a
b
c
d
例2 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB,D为PB的中点,求证:
(1)AD⊥BC (2)PC ⊥AD
P
A
B
C
D
P66 探究:
如图,直四棱柱A’B’C’D’-ABCD中,底面四边形ABCD满足什么条件时,A’C⊥B’D’?
1、如图,在正方体ABCD-A1B1C1D1中,
(1)请列举与平面ABCD垂直的直线 ;
(2)你还能找出一条与平面D1DBB1垂直的直线吗?
A
B
C
D
A1
B1
C1
D1
课堂检测
思考:你还能找出一条与平面A1C1B垂直的直线吗?
思考:直线与平面有哪些位置关系?
α
a
A
垂直
斜交
问题探究(三):平面的斜线
思考:当直线与平面相交时,它们可能垂直,也可能不垂直,如果一条直线和一个平面相交但不垂直,这条直线叫做这个平面的斜线,斜线和平面的交点叫做斜足.那么过一点作一个平面的斜线有多少条?
α
l
P
斜线
斜足
思考:过斜线上斜足外一点向平面引垂线,连结垂足和斜足的直线叫做这条斜线在这个平面上的射影.那么斜线l在平面α内的射影有几条?
α
l
P
A
B
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
O
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
E
巩固练习
思考:如图,过平面α外一点P引平面α的两条斜线段PA、PB,斜足为A、B,再过点P引平面α的垂线,垂足为O,如果PA>PB,那么OA与OB的大小关系如何?反之成立吗?
α
O
P
A
B
思考:如图,直线l是平面α的一条斜线,它在平面α内的射影为b,直线a在平面α内,如果a⊥b,那么直线a与直线l垂直吗?为什么?反之成立吗?
a
α
l
b
思考:我们把平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角.在实际应用或解题中,怎样去求这个角?
α
P
A
B
线面所成的角:
(1)斜线与平面所成的角:
规定:平面一条斜线与它在平面上的射影所成的锐角,称为这条直线与这个平面所成的角。
范围:
(2)垂线与平面所成的角为:
(3)规定:当l∥α 或l在α 内时,
l与α 所成的角为:
(0°,90°)
90°
0°
α
A
P
O
例题讲解
例3 在正方体ABCD-A1B1C1D1中.
(1)求直线A1B和平面ABCD所成的角;
(2)求直线A1B和平面A1B1CD所成的角.
D1
A
B
A1
C
B1
C1
D
O
归纳小结
1.直线与平面垂直的概念
(1)利用定义;
(2)利用判定定理.
3.数学思想方法:转化的思想
空间问题
平面问题
3.直线与平面垂直的判定
线线垂直
线面垂直
垂直于平面内任意一条直线
2. 线面角的概念及范围
