2020—2021学年人教版高一数学《2.1.1指数概念的扩充》课件(21张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《2.1.1指数概念的扩充》课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 21:04:56 | ||
图片预览






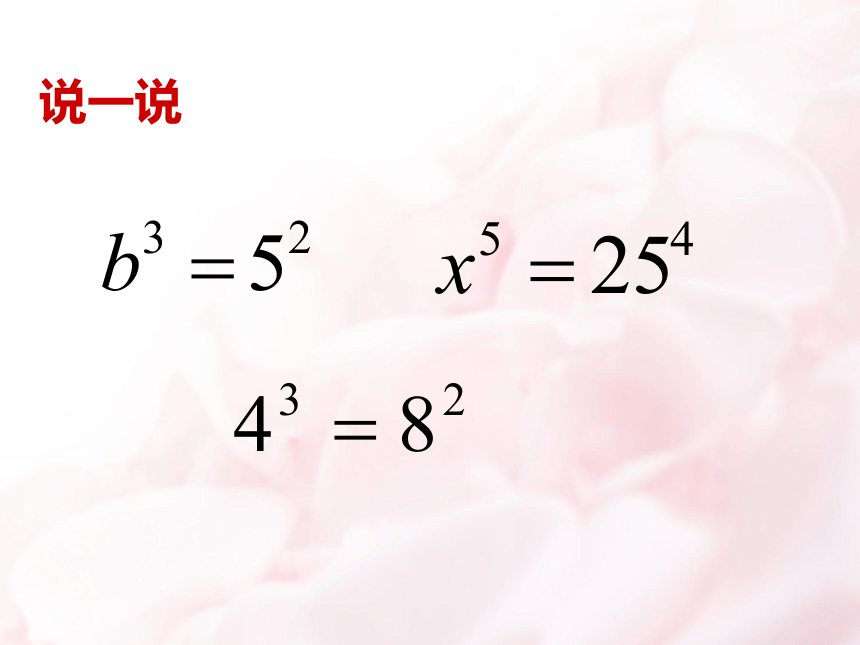

文档简介
数学组 王路
复习
整数指数幂
整数指数幂的运算性质
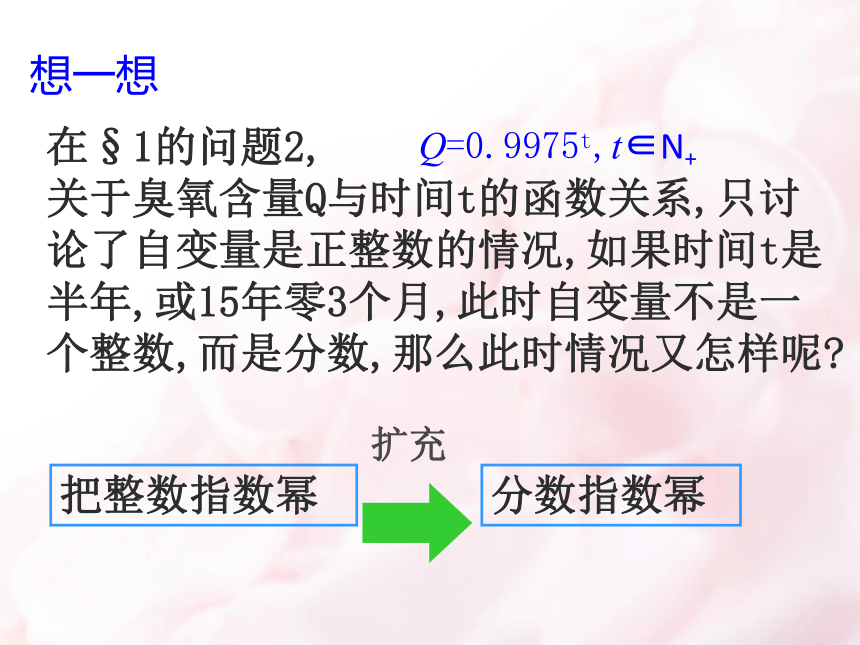
在§1的问题2,
关于臭氧含量Q与时间t的函数关系,只讨论了自变量是正整数的情况,如果时间t是半年,或15年零3个月,此时自变量不是一个整数,而是分数,那么此时情况又怎样呢?
把整数指数幂
分数指数幂
扩充
想一想
Q=0.9975t,t∈N+
问题1:在正整数指数幂的运算bn=a中,已知正实数a和正整数n,如何求b?
说一说
一般地,给定正实数a,对于任意给定的正整数n,存在唯一的正实数b,使得bn=a,我们把b叫作
a的 次幂,记作
问题2:在bn= am中,已知正实数a和正整数m,n,如何求b?
一般地,给定正实数a,对于任意给定的整数m,n( m,n互素),存在唯一的正实数b,使得bn=am,我们把b叫
作a的 次幂,记作
说一说
例题讲解
例1 把下列各式中的b写成正分数指数幂的形式.
例题讲解
例2 计算
有时我们把正分数指数幂写成根式形式
写一写
(2)
(3)
(4)
(5)
(6)
(1)
正数的负分数指数幂的意义与负整数指数幂的意义相仿,即
0的正分数指数幂等于0,
0的负分数指数幂无意义.
整数指数幂
有理数指数幂
扩充
例3 把下列各式中的b写成负分数指数幂的形式
整数指数幂的运算性质在有理数幂也适用
练习
2.化简(式中字母均为正数)
例4 计算下列根式
指数也可以扩充到实数
有理数指数幂的运算性质在实数幂也适用
若a>0,α是实数,则aα>0
不等性质
小结
复习
整数指数幂
整数指数幂的运算性质
在§1的问题2,
关于臭氧含量Q与时间t的函数关系,只讨论了自变量是正整数的情况,如果时间t是半年,或15年零3个月,此时自变量不是一个整数,而是分数,那么此时情况又怎样呢?
把整数指数幂
分数指数幂
扩充
想一想
Q=0.9975t,t∈N+
问题1:在正整数指数幂的运算bn=a中,已知正实数a和正整数n,如何求b?
说一说
一般地,给定正实数a,对于任意给定的正整数n,存在唯一的正实数b,使得bn=a,我们把b叫作
a的 次幂,记作
问题2:在bn= am中,已知正实数a和正整数m,n,如何求b?
一般地,给定正实数a,对于任意给定的整数m,n( m,n互素),存在唯一的正实数b,使得bn=am,我们把b叫
作a的 次幂,记作
说一说
例题讲解
例1 把下列各式中的b写成正分数指数幂的形式.
例题讲解
例2 计算
有时我们把正分数指数幂写成根式形式
写一写
(2)
(3)
(4)
(5)
(6)
(1)
正数的负分数指数幂的意义与负整数指数幂的意义相仿,即
0的正分数指数幂等于0,
0的负分数指数幂无意义.
整数指数幂
有理数指数幂
扩充
例3 把下列各式中的b写成负分数指数幂的形式
整数指数幂的运算性质在有理数幂也适用
练习
2.化简(式中字母均为正数)
例4 计算下列根式
指数也可以扩充到实数
有理数指数幂的运算性质在实数幂也适用
若a>0,α是实数,则aα>0
不等性质
小结
