2020—2021学年人教版高一数学《2.1.2指数函数》课件(20张PPT)
文档属性
| 名称 | 2020—2021学年人教版高一数学《2.1.2指数函数》课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 430.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览








文档简介
指数函数
问题1:
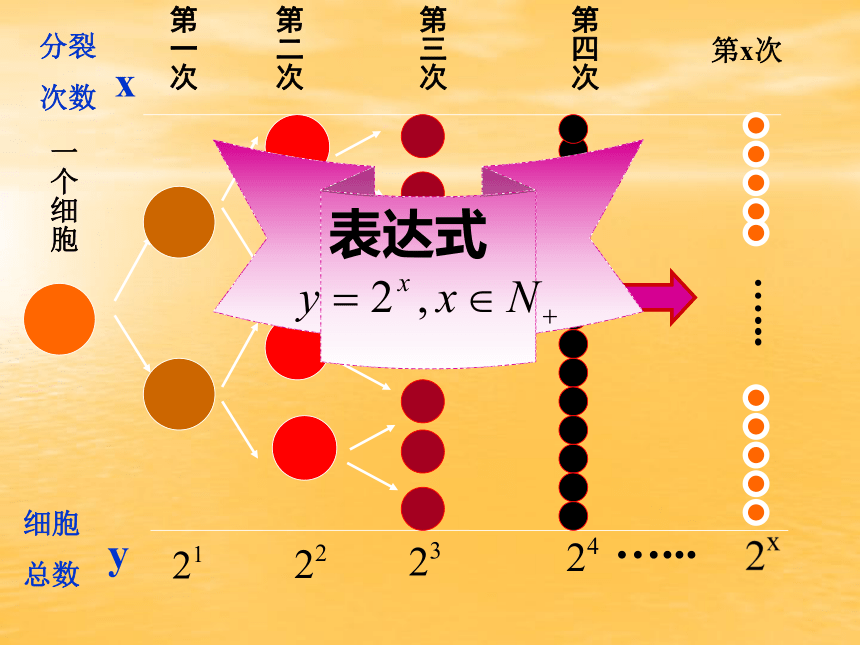
某种细胞分裂时,由一个分裂成2个,2个
分裂成4个……,请你写出1个这样的细胞分裂x
次后,细胞个数y与x的函数关系式。
一个细胞
分裂
次数
第一次
第二次
第三次
第四次
第x次
…...
细胞
总数
y
…...
表达式
x
截取
次数
木棰
剩余
1次
2次
3次
4次
x次
问题2:《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。”请你写出截取x次后,木棰剩余量 y 关于 x 的函数关系式?
我们得到下面两个函数:
思考1 以上两个函数有何共同特征?
(1)幂的形式
(2)底数是常数
(3)指数为自变量
思考2:
像 这样的函数与我们学过的
这样的函数一样吗?有什么区别?
答:不一样。前一个函数的自变量在指数位置上,而底数为常数;后三个函数的自变量在底数位置上,指数为常数。
指数函数的定义:
一般地,函数 叫做指数函数,其中 x 是自变量, 函数的定义域是 R。
判断一个函数是否为指数函数的依据:
是否是形如 的函数,其中系数为1,底数满足 ,指数位置上是自变量x。
问题:在函数
为什么规定 呢?
想一想:
练一练
注意:指数函数 中,
① 前的系数必须1。
② x在指数的位置上。
③ a是大于0且不等于1的常数。
合作探究一
指数函数 的图像特征的学习
x
4
3
2
1
0
-1
-2
-3
-4
1
2
3
4
5
6
7
8
y
x
y
-3
1\8
-2
1\4
-1
1\2
0
1
1
2
2
4
3
8
x
y
-3
8
-2
4
-1
2
0
1
1
1\2
2
1\4
3
1\8
合作探究二
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
a>1
0R
( 0 , + ∞ )
( 0 , 1 )
增函数
减函数
指数函数 的图像及性质
当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
单 调 性 :
奇 偶 性 :
非奇非偶函数
过定点 :
例3 比较下列各题中两个值的大小:
解:考察函数
3 0.6 5 0.6
0.6
x
y
0
1
y=3 x
y=5 x
小结:
(1)当底数相同,指数不同时,可以构造一个指数函数, 利用指数函数的单调性求解
(2)当底数不同,指数不同时,通常以“1”为桥 梁,进行比较大小
(3)当底数不同,指数相同时,可根据图象进行研究
合作探究三
x
4
3
2
1
0
-1
-2
-3
-4
1
2
3
4
5
6
7
8
y
几何画板
0
1
判断a,b,c,d的大小关系。
X=1
从下往上,
底数越来越大
五:课时小结
本节课讲了指数函数的定义、图像及性质,要理解并灵活掌握,另外本节在应用上主要讲了判定大小的应用,要灵活应用性质及图像来判定大小
数学是人类最高超的成就,
也是人类心灵最独特的创作。
音乐能激发或抚慰情怀,
绘画使人赏心悦目,
诗歌能动人心弦,
哲学使人获得智慧 ,
科学可改善物质生活,
但数学能给予以上的一切。
问题1:
某种细胞分裂时,由一个分裂成2个,2个
分裂成4个……,请你写出1个这样的细胞分裂x
次后,细胞个数y与x的函数关系式。
一个细胞
分裂
次数
第一次
第二次
第三次
第四次
第x次
…...
细胞
总数
y
…...
表达式
x
截取
次数
木棰
剩余
1次
2次
3次
4次
x次
问题2:《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。”请你写出截取x次后,木棰剩余量 y 关于 x 的函数关系式?
我们得到下面两个函数:
思考1 以上两个函数有何共同特征?
(1)幂的形式
(2)底数是常数
(3)指数为自变量
思考2:
像 这样的函数与我们学过的
这样的函数一样吗?有什么区别?
答:不一样。前一个函数的自变量在指数位置上,而底数为常数;后三个函数的自变量在底数位置上,指数为常数。
指数函数的定义:
一般地,函数 叫做指数函数,其中 x 是自变量, 函数的定义域是 R。
判断一个函数是否为指数函数的依据:
是否是形如 的函数,其中系数为1,底数满足 ,指数位置上是自变量x。
问题:在函数
为什么规定 呢?
想一想:
练一练
注意:指数函数 中,
① 前的系数必须1。
② x在指数的位置上。
③ a是大于0且不等于1的常数。
合作探究一
指数函数 的图像特征的学习
x
4
3
2
1
0
-1
-2
-3
-4
1
2
3
4
5
6
7
8
y
x
y
-3
1\8
-2
1\4
-1
1\2
0
1
1
2
2
4
3
8
x
y
-3
8
-2
4
-1
2
0
1
1
1\2
2
1\4
3
1\8
合作探究二
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
a>1
0
( 0 , + ∞ )
( 0 , 1 )
增函数
减函数
指数函数 的图像及性质
当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
单 调 性 :
奇 偶 性 :
非奇非偶函数
过定点 :
例3 比较下列各题中两个值的大小:
解:考察函数
3 0.6 5 0.6
0.6
x
y
0
1
y=3 x
y=5 x
小结:
(1)当底数相同,指数不同时,可以构造一个指数函数, 利用指数函数的单调性求解
(2)当底数不同,指数不同时,通常以“1”为桥 梁,进行比较大小
(3)当底数不同,指数相同时,可根据图象进行研究
合作探究三
x
4
3
2
1
0
-1
-2
-3
-4
1
2
3
4
5
6
7
8
y
几何画板
0
1
判断a,b,c,d的大小关系。
X=1
从下往上,
底数越来越大
五:课时小结
本节课讲了指数函数的定义、图像及性质,要理解并灵活掌握,另外本节在应用上主要讲了判定大小的应用,要灵活应用性质及图像来判定大小
数学是人类最高超的成就,
也是人类心灵最独特的创作。
音乐能激发或抚慰情怀,
绘画使人赏心悦目,
诗歌能动人心弦,
哲学使人获得智慧 ,
科学可改善物质生活,
但数学能给予以上的一切。
