6.4.3余弦定理、正弦定理第三课时 余弦定理和正弦定理应用举例-【新教材】人教A版(2019)高中数学必修第二册同步讲义
文档属性
| 名称 | 6.4.3余弦定理、正弦定理第三课时 余弦定理和正弦定理应用举例-【新教材】人教A版(2019)高中数学必修第二册同步讲义 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 21:41:57 | ||
图片预览




文档简介
第六章
平面向量及其应用
6.4.3
余弦定理、正弦定理
第三课时
余弦定理和正弦定理应用举例
【课程标准】
能用余弦定理、正弦定理解决简单的实际问题
【知识要点归纳】
把实际问题中的条件和所要求的结果转化为三角形中的已知和未知的角和边,通过建立数学模型来求解,具体步骤如下:
在解三角形的实际应用问题中,作图是关键一步,只有根据实际问题做出准确的图形,才能如实的反映实际情况,才能将实际问题抽象为解三角形的数学模型,才能正确解决问题。
注意几点:
1.准确把握实际测量中的有关名词和术语,例如方向角和方位角的区别
2.将空间问题转化为平面问题
3.恰当构造三角形
【经典例题】
例1.如图所示,为测一树的高度,在地面上选取、两点,从、两点分别测得树尖的仰角为,,且、两点间的距离为,则树的高度为
A.
B.
C.
D.
例2.如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在点测得公路北侧山顶的仰角为,汽车行驶后到达点测得山顶恰好在正北方,且仰角为,则山的高度为
A.
B.
C.
D.
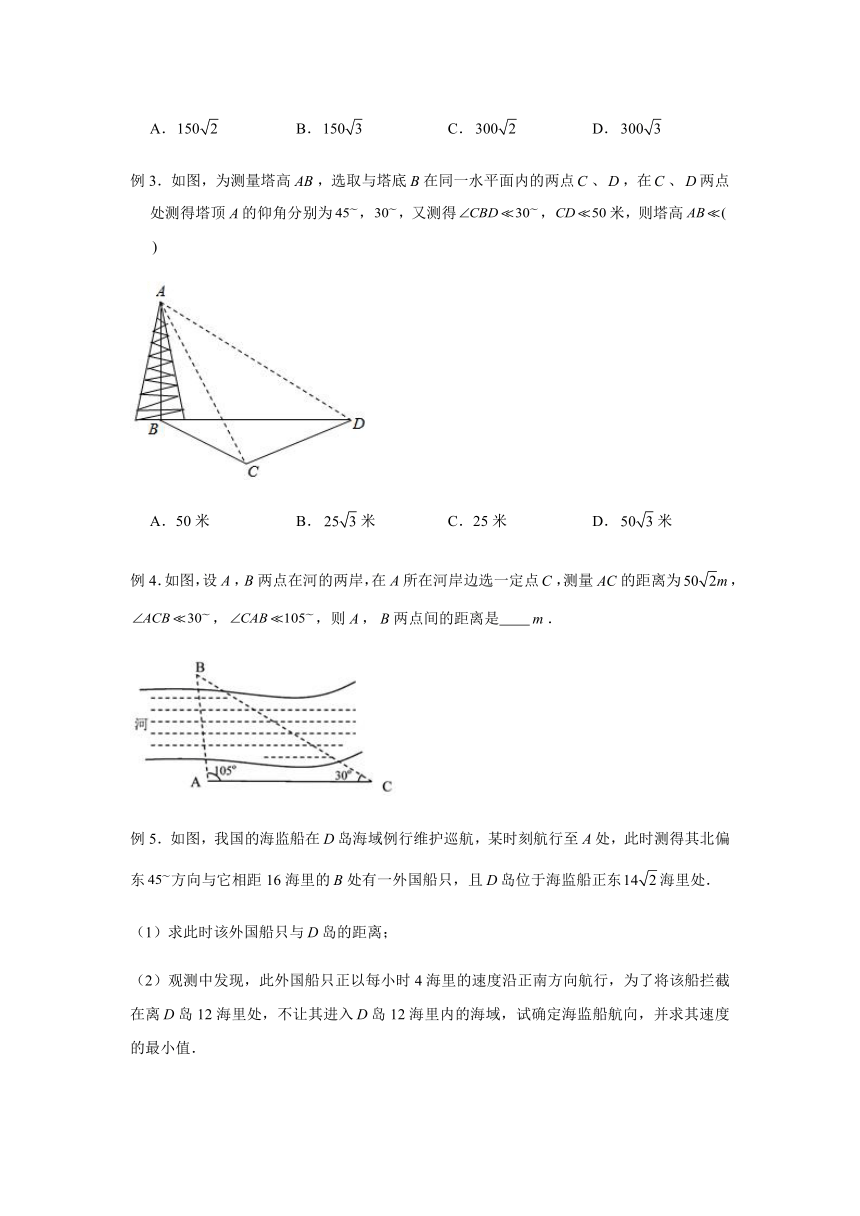
例3.如图,为测量塔高,选取与塔底在同一水平面内的两点、,在、两点处测得塔顶的仰角分别为,,又测得,米,则塔高
A.50米
B.米
C.25米
D.米
例4.如图,设,两点在河的两岸,在所在河岸边选一定点,测量的距离为,,,则,两点间的距离是 .
例5.如图,我国的海监船在岛海域例行维护巡航,某时刻航行至处,此时测得其北偏东方向与它相距16海里的处有一外国船只,且岛位于海监船正东海里处.
(1)求此时该外国船只与岛的距离;
(2)观测中发现,此外国船只正以每小时4海里的速度沿正南方向航行,为了将该船拦截在离岛12海里处,不让其进入岛12海里内的海域,试确定海监船航向,并求其速度的最小值.
【当堂检测】
一.选择题(共6小题)
1.如图,为测得河对岸塔的高,先在河岸上选一点,使在塔底的正东方向上,测得点的仰角为,再由点沿北偏东方向走到位置,测得,则塔的高是(单位:
A.
B.
C.
D.13
2.如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得米,米,米,,,据此可以估计天坛的最下面一层的直径大约为 (结果精确到1米)
(参考数据:,,,
A.39米
B.43米
C.49米
D.53米
3.珠穆朗玛峰是印度洋板块和欧亚板块碰撞挤压形成的.这种挤压一直在进行,珠穆朗玛峰的高度也一直在变化.由于地势险峻,气候恶劣,通常采用人工攀登的方式为珠峰“量身高”.攀登者们肩负高精度测量仪器,采用了分段测量的方法,从山脚开始,直到到达山顶,再把所有的高度差累加,就会得到珠峰的高度.2020年5月,中国珠峰高程测量登山队8名队员开始新一轮的珠峰测量工作.如图,在测量过程中,已知竖立在点处的测量觇标高12米,攀登者们在处测得到觇标底点和顶点的仰角分别为,,则、的高度差为
A.米
B.6米
C.米
D.12米
4.如图,在点和点测得淮安电视塔塔顶的仰角分别为和(点、与塔底在同一直线上)又测得米,根据所测数据可求得淮安电视塔的高度为
A.米
B.米
C.米
D.320米
5.三国年年)是上承东汉下启西晋的一段历史时期,分为曹魏、蜀汉、东吴三个政权.元末明初的小说家罗贯中依据这段历史编写《三国演义》全名为《三国志通俗演义》,小说中记载孙刘联盟共同打击曹魏,蜀吴两国为了达成合作经常派使臣来往,古代出行以骑马为主,假如一匹马每个时辰能走30公里,一天最多能跑10个小时,十天能到达.吴国都城位于蜀国都城正东,魏国的都城在蜀国都城的北偏东,相距约1000公里,若吴国一叛徒要向魏国告密大约需要几天能达到魏国都城
A.七
B.八
C.九
D.十
6.某船在处测得灯塔在其南偏东方向上,该船继续向正南方向行驶5海里到处,测得灯塔在其北偏东方向上,然后该船向东偏南方向行驶2海里到处,此时船到灯塔的距离为多少海里
A.千米
B.千米
C.6千米
D.5千米
二.填空题(共2小题)
7.如图,小明在山脚测得山顶的仰角为,在山脚测得山顶的仰角为,测得,,间的距离为,,已知山脚和,在同一水平面上,则山的高度 .
8.某地计划建一个游乐场,规划游乐场为如图所示的四边形区域,其中三角形区域中,百米,百米,三角形区域是以为斜边的等腰直角三角形,现计划将三角形区域建为水上项目区,则三角形区域的最大面积为 平方百米.
三.解答题(共4小题)
9.已知是底部不可到达的建筑物,是建筑物的最高点,为测量建筑物的高度,先把高度为1.5米的测角仪放置在位置,测得的仰角为,再把测角仪放置在位置,测得的仰角为,已知米,,,在同一水平线上,求建筑物的高度.
10.如图,甲船在处,乙船在处的南偏东方向,距有15海里的处,并以25海里每小时的速度沿南偏西方向行驶,若甲船沿南偏东度的方向,并以35海里每小时的速度行驶,若两船同时出发,并在小时后在处相遇.
(Ⅰ)求的值;
(Ⅱ)求的值.(结果保留根号,无需求近似值)
11.小明在东方明珠广播电视塔底端的正东方向上的处,沿着与电视塔垂直的水平马路驾驶机动车行驶,以南偏西的方向每小时60千米的速度开了15分钟以后,在点处望见电视塔的底端在东北方向上,设沿途处观察电视塔的仰角,的最大值为.
(1)小明开车从处出发到处,几小时后其所在位置观察电视塔的仰角达到最大值,约为多少分钟?(分钟保留两位小数)
(2)求东方明珠塔的高度约为多少米.(保留两位小数)
12.如图,海岛、相距海里,上午9点整,有一客轮在海岛的北偏西,且距海岛海里的处,沿直线方向匀速开往海岛,在海岛停留10分钟后前往市,上午,测得客轮位于海岛的北偏西,且距海岛海里的处,此时小张从海岛乘坐速度为海里小时的小艇沿直线方向前往岛换成客轮去往市,其中,.
(1)问小张能否乘上这班客轮?说明理由;
(2)现测得,,已知速度为的小艇每小时的费用为元,若小张由海岛直接乘小艇去往市,则至少需要多少费用?(结果近似到元)
参考答案与试题解析
一.选择题(共3小题)
1.【解答】解:在,,,,
由正弦定理得:,,
树的高度为,
答:树的高度为.
故选:.
2.【解答】解:设此山高,由题意得,
在中,,,.
根据勾股定理得,,
故选:.
3.【解答】解:设,则,,
,米,
,
.
故选:.
二.填空题(共1小题)
4.【解答】解:,,,
在三角形中,由正弦定理,得,
,
、两点的距离为,
故答案为:50.
三.解答题(共1小题)
5.【解答】解:(1)根据余弦定理可得:
,
则(海里);
(2)过作于,则,所以,
以为圆心,12为半径作圆交于点,连接,,
则,,,
所以,
外国船只到达点的时间,
所以,海盗船速度,
所以,海盗船就以北偏东方向,速度大于20海里小时,才能拦截.
参考答案与试题解析
一.选择题(共6小题)
1.【解答】解:在中,根据题意知:,,,所以
利用正弦定理:,解得,
在中,,解得.
故选:.
2.【解答】解:在中,,,,所以,
在中,,
所以(米.
故选:.
3.【解答】解:根据题意画出如图的模型,则,,
,所以,,
可得所以,
所以在中,(米.
故选:.
4.【解答】解:在中,,所以;
在中,,所以,
解得;
又,且,
所以,
解得;
即电视塔的高度为(米.
故选:.
5.【解答】解:可以把魏蜀吴三国的都城位置分别即为,,,
由题意可知公里,公里,,
由余弦定理得公里,
(天,
故叛徒大约九天能到达目的地.
故选:.
6.【解答】解:在中,,,,
可得为等边三角形,可得,
在中,,,,
则,
故选:.
二.填空题(共2小题)
7.【解答】解:在中,设,
利用解直角三角形知识,
在中,,
在中,利用余弦定理,
解得或50,
当时,,不合题意,
故.
故答案为:
8.【解答】解:建立平面直角坐标系,如图所示,
设,,
则点的坐标为,
所以,
易知点在以为圆心,2为半径的圆上,
设,,
则点的坐标为,
所以,当且仅当时,的面积最大,最大为平方百米.
故答案为:.
三.解答题(共4小题)
9.【解答】解:中,由正弦定理得,
(米;
在中,;
;
所以,
即建筑物的高度为米.
故答案为:.
10.【解答】解:(Ⅰ)如图所示,
在中,,,,.
由余弦定理得:,
整理得,
解得或(舍去);
所以.
(Ⅱ)中,,,
根据正弦定理得,,
即,
所以,
所以
.
11.【解答】解:(1)依题意知在中,,
,,
由正弦定理得,
,
在中,,
为定长,可得当的长最小时,取最大值,这时,
当时,在中,可得:,
设该人沿南偏西的方向走到仰角最大时,走了分钟,
则(分钟),
(2)由(1)知当取得最大值时,,在中,,
米.
即所求塔高为4754.81米.
12.【解答】解:(1)根据题意得:.
在
中,由余弦定理得,
,
所以客轮的航行速度
海里小时),
因为,所以,
所以.
在,由余弦定理得,,
整理得:,
解得
或
(舍去.
所以客轮从
处到岛
所用的时间
小时
小张到岛
所用的时间至少为
小时.
由于
所以若小张9点半出发,则无法乘上这班客轮.
(2)在
中,
所以
为锐角,.
所以
,
由正弦定理得,,
所以,
所以小张由岛
直接乘小艇去城市
的总费用为
当且仅当,即
时
(元,
所以若小张由岛
直接乘小艇去
市,其费用至少需
元.
平面向量及其应用
6.4.3
余弦定理、正弦定理
第三课时
余弦定理和正弦定理应用举例
【课程标准】
能用余弦定理、正弦定理解决简单的实际问题
【知识要点归纳】
把实际问题中的条件和所要求的结果转化为三角形中的已知和未知的角和边,通过建立数学模型来求解,具体步骤如下:
在解三角形的实际应用问题中,作图是关键一步,只有根据实际问题做出准确的图形,才能如实的反映实际情况,才能将实际问题抽象为解三角形的数学模型,才能正确解决问题。
注意几点:
1.准确把握实际测量中的有关名词和术语,例如方向角和方位角的区别
2.将空间问题转化为平面问题
3.恰当构造三角形
【经典例题】
例1.如图所示,为测一树的高度,在地面上选取、两点,从、两点分别测得树尖的仰角为,,且、两点间的距离为,则树的高度为
A.
B.
C.
D.
例2.如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在点测得公路北侧山顶的仰角为,汽车行驶后到达点测得山顶恰好在正北方,且仰角为,则山的高度为
A.
B.
C.
D.
例3.如图,为测量塔高,选取与塔底在同一水平面内的两点、,在、两点处测得塔顶的仰角分别为,,又测得,米,则塔高
A.50米
B.米
C.25米
D.米
例4.如图,设,两点在河的两岸,在所在河岸边选一定点,测量的距离为,,,则,两点间的距离是 .
例5.如图,我国的海监船在岛海域例行维护巡航,某时刻航行至处,此时测得其北偏东方向与它相距16海里的处有一外国船只,且岛位于海监船正东海里处.
(1)求此时该外国船只与岛的距离;
(2)观测中发现,此外国船只正以每小时4海里的速度沿正南方向航行,为了将该船拦截在离岛12海里处,不让其进入岛12海里内的海域,试确定海监船航向,并求其速度的最小值.
【当堂检测】
一.选择题(共6小题)
1.如图,为测得河对岸塔的高,先在河岸上选一点,使在塔底的正东方向上,测得点的仰角为,再由点沿北偏东方向走到位置,测得,则塔的高是(单位:
A.
B.
C.
D.13
2.如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得米,米,米,,,据此可以估计天坛的最下面一层的直径大约为 (结果精确到1米)
(参考数据:,,,
A.39米
B.43米
C.49米
D.53米
3.珠穆朗玛峰是印度洋板块和欧亚板块碰撞挤压形成的.这种挤压一直在进行,珠穆朗玛峰的高度也一直在变化.由于地势险峻,气候恶劣,通常采用人工攀登的方式为珠峰“量身高”.攀登者们肩负高精度测量仪器,采用了分段测量的方法,从山脚开始,直到到达山顶,再把所有的高度差累加,就会得到珠峰的高度.2020年5月,中国珠峰高程测量登山队8名队员开始新一轮的珠峰测量工作.如图,在测量过程中,已知竖立在点处的测量觇标高12米,攀登者们在处测得到觇标底点和顶点的仰角分别为,,则、的高度差为
A.米
B.6米
C.米
D.12米
4.如图,在点和点测得淮安电视塔塔顶的仰角分别为和(点、与塔底在同一直线上)又测得米,根据所测数据可求得淮安电视塔的高度为
A.米
B.米
C.米
D.320米
5.三国年年)是上承东汉下启西晋的一段历史时期,分为曹魏、蜀汉、东吴三个政权.元末明初的小说家罗贯中依据这段历史编写《三国演义》全名为《三国志通俗演义》,小说中记载孙刘联盟共同打击曹魏,蜀吴两国为了达成合作经常派使臣来往,古代出行以骑马为主,假如一匹马每个时辰能走30公里,一天最多能跑10个小时,十天能到达.吴国都城位于蜀国都城正东,魏国的都城在蜀国都城的北偏东,相距约1000公里,若吴国一叛徒要向魏国告密大约需要几天能达到魏国都城
A.七
B.八
C.九
D.十
6.某船在处测得灯塔在其南偏东方向上,该船继续向正南方向行驶5海里到处,测得灯塔在其北偏东方向上,然后该船向东偏南方向行驶2海里到处,此时船到灯塔的距离为多少海里
A.千米
B.千米
C.6千米
D.5千米
二.填空题(共2小题)
7.如图,小明在山脚测得山顶的仰角为,在山脚测得山顶的仰角为,测得,,间的距离为,,已知山脚和,在同一水平面上,则山的高度 .
8.某地计划建一个游乐场,规划游乐场为如图所示的四边形区域,其中三角形区域中,百米,百米,三角形区域是以为斜边的等腰直角三角形,现计划将三角形区域建为水上项目区,则三角形区域的最大面积为 平方百米.
三.解答题(共4小题)
9.已知是底部不可到达的建筑物,是建筑物的最高点,为测量建筑物的高度,先把高度为1.5米的测角仪放置在位置,测得的仰角为,再把测角仪放置在位置,测得的仰角为,已知米,,,在同一水平线上,求建筑物的高度.
10.如图,甲船在处,乙船在处的南偏东方向,距有15海里的处,并以25海里每小时的速度沿南偏西方向行驶,若甲船沿南偏东度的方向,并以35海里每小时的速度行驶,若两船同时出发,并在小时后在处相遇.
(Ⅰ)求的值;
(Ⅱ)求的值.(结果保留根号,无需求近似值)
11.小明在东方明珠广播电视塔底端的正东方向上的处,沿着与电视塔垂直的水平马路驾驶机动车行驶,以南偏西的方向每小时60千米的速度开了15分钟以后,在点处望见电视塔的底端在东北方向上,设沿途处观察电视塔的仰角,的最大值为.
(1)小明开车从处出发到处,几小时后其所在位置观察电视塔的仰角达到最大值,约为多少分钟?(分钟保留两位小数)
(2)求东方明珠塔的高度约为多少米.(保留两位小数)
12.如图,海岛、相距海里,上午9点整,有一客轮在海岛的北偏西,且距海岛海里的处,沿直线方向匀速开往海岛,在海岛停留10分钟后前往市,上午,测得客轮位于海岛的北偏西,且距海岛海里的处,此时小张从海岛乘坐速度为海里小时的小艇沿直线方向前往岛换成客轮去往市,其中,.
(1)问小张能否乘上这班客轮?说明理由;
(2)现测得,,已知速度为的小艇每小时的费用为元,若小张由海岛直接乘小艇去往市,则至少需要多少费用?(结果近似到元)
参考答案与试题解析
一.选择题(共3小题)
1.【解答】解:在,,,,
由正弦定理得:,,
树的高度为,
答:树的高度为.
故选:.
2.【解答】解:设此山高,由题意得,
在中,,,.
根据勾股定理得,,
故选:.
3.【解答】解:设,则,,
,米,
,
.
故选:.
二.填空题(共1小题)
4.【解答】解:,,,
在三角形中,由正弦定理,得,
,
、两点的距离为,
故答案为:50.
三.解答题(共1小题)
5.【解答】解:(1)根据余弦定理可得:
,
则(海里);
(2)过作于,则,所以,
以为圆心,12为半径作圆交于点,连接,,
则,,,
所以,
外国船只到达点的时间,
所以,海盗船速度,
所以,海盗船就以北偏东方向,速度大于20海里小时,才能拦截.
参考答案与试题解析
一.选择题(共6小题)
1.【解答】解:在中,根据题意知:,,,所以
利用正弦定理:,解得,
在中,,解得.
故选:.
2.【解答】解:在中,,,,所以,
在中,,
所以(米.
故选:.
3.【解答】解:根据题意画出如图的模型,则,,
,所以,,
可得所以,
所以在中,(米.
故选:.
4.【解答】解:在中,,所以;
在中,,所以,
解得;
又,且,
所以,
解得;
即电视塔的高度为(米.
故选:.
5.【解答】解:可以把魏蜀吴三国的都城位置分别即为,,,
由题意可知公里,公里,,
由余弦定理得公里,
(天,
故叛徒大约九天能到达目的地.
故选:.
6.【解答】解:在中,,,,
可得为等边三角形,可得,
在中,,,,
则,
故选:.
二.填空题(共2小题)
7.【解答】解:在中,设,
利用解直角三角形知识,
在中,,
在中,利用余弦定理,
解得或50,
当时,,不合题意,
故.
故答案为:
8.【解答】解:建立平面直角坐标系,如图所示,
设,,
则点的坐标为,
所以,
易知点在以为圆心,2为半径的圆上,
设,,
则点的坐标为,
所以,当且仅当时,的面积最大,最大为平方百米.
故答案为:.
三.解答题(共4小题)
9.【解答】解:中,由正弦定理得,
(米;
在中,;
;
所以,
即建筑物的高度为米.
故答案为:.
10.【解答】解:(Ⅰ)如图所示,
在中,,,,.
由余弦定理得:,
整理得,
解得或(舍去);
所以.
(Ⅱ)中,,,
根据正弦定理得,,
即,
所以,
所以
.
11.【解答】解:(1)依题意知在中,,
,,
由正弦定理得,
,
在中,,
为定长,可得当的长最小时,取最大值,这时,
当时,在中,可得:,
设该人沿南偏西的方向走到仰角最大时,走了分钟,
则(分钟),
(2)由(1)知当取得最大值时,,在中,,
米.
即所求塔高为4754.81米.
12.【解答】解:(1)根据题意得:.
在
中,由余弦定理得,
,
所以客轮的航行速度
海里小时),
因为,所以,
所以.
在,由余弦定理得,,
整理得:,
解得
或
(舍去.
所以客轮从
处到岛
所用的时间
小时
小张到岛
所用的时间至少为
小时.
由于
所以若小张9点半出发,则无法乘上这班客轮.
(2)在
中,
所以
为锐角,.
所以
,
由正弦定理得,,
所以,
所以小张由岛
直接乘小艇去城市
的总费用为
当且仅当,即
时
(元,
所以若小张由岛
直接乘小艇去
市,其费用至少需
元.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
