2020—2021学年北师大版七年级数学下册 第二章《相交线与平行线》全章质量评估过关卷(Word版 含答案)
文档属性
| 名称 | 2020—2021学年北师大版七年级数学下册 第二章《相交线与平行线》全章质量评估过关卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 11:44:43 | ||
图片预览


文档简介
北师大版七年级数学第二学期第二章《相交线与平行线》全章质量评估过关卷
一、单选题
1.下列说法正确的是( )
(1)如果互余的两个角的度数之比为,那么这两个角分别为和
(2)如果两个角是同一个角的补角,那么这两个角不一定相等
(3)如果两个角的度数分别是和,那么这两个角互余
(4)一个锐角的余角比这个锐角的补角小
A.个 B.个 C.个 D.个
2.如图,直线a,b被直线c所截,现给出下列四个条件:(1);(2);(3);(4),其中能判定的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
3.如图,已知直线,平分交直线于点,若,则等于( )
A.25° B.29° C.30° D.45°
4.用直尺和圆规作∠HDG=∠AOB的过程,弧①是( )
A.以D为圆心,以DN为半径画弧
B.以D为圆心,以EF为半径画弧
C.以M为圆心,以DN为半径画弧
D.以M为圆心,以EF为半径画弧
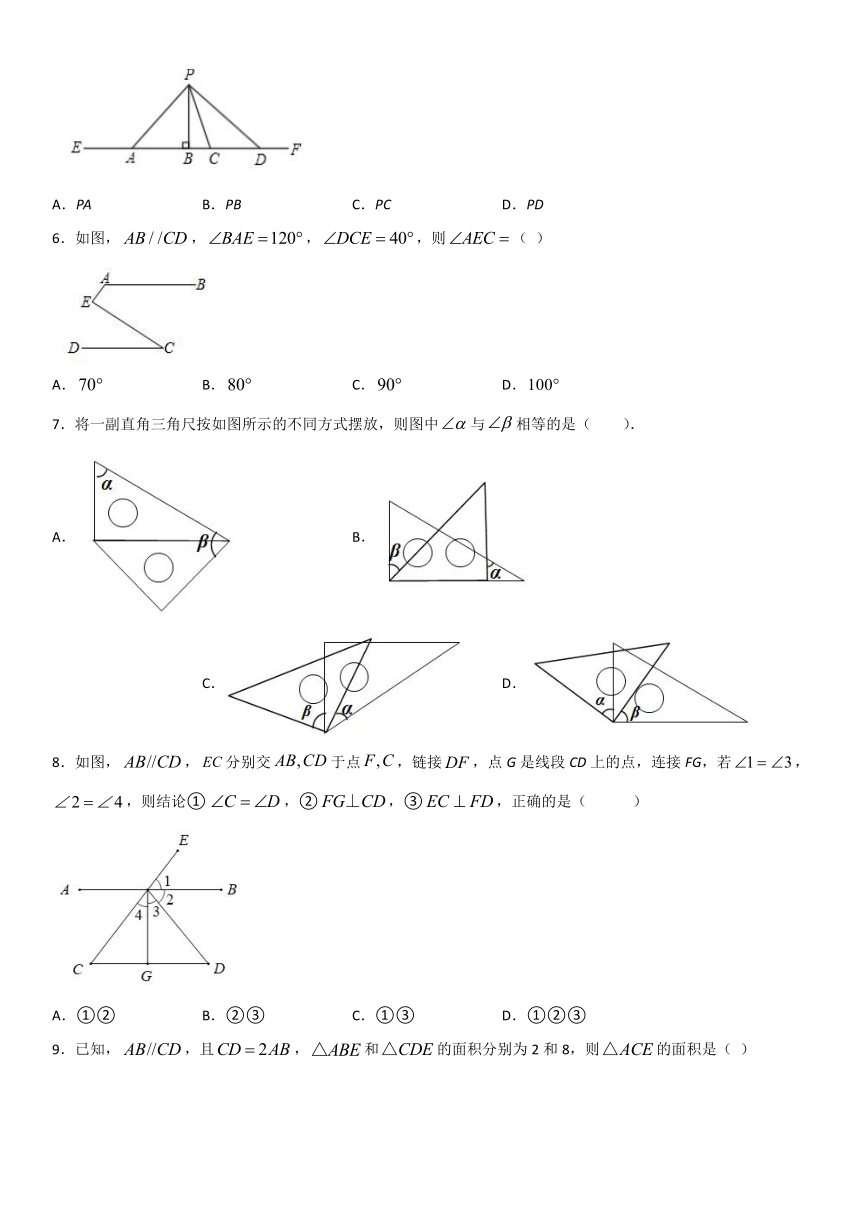
5.如图,从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的是( )
A.PA B.PB C.PC D.PD
6.如图,,,,则( )
A. B. C. D.
7.将一副直角三角尺按如图所示的不同方式摆放,则图中与相等的是( ).
A. B. C. D.
8.如图,,分别交于点,链接,点G是线段CD上的点,连接FG,若,,则结论①,②,③,正确的是( )
A.①② B.②③ C.①③ D.①②③
9.已知,,且,和的面积分别为2和8,则的面积是( )
A.3 B.4 C.5 D.6
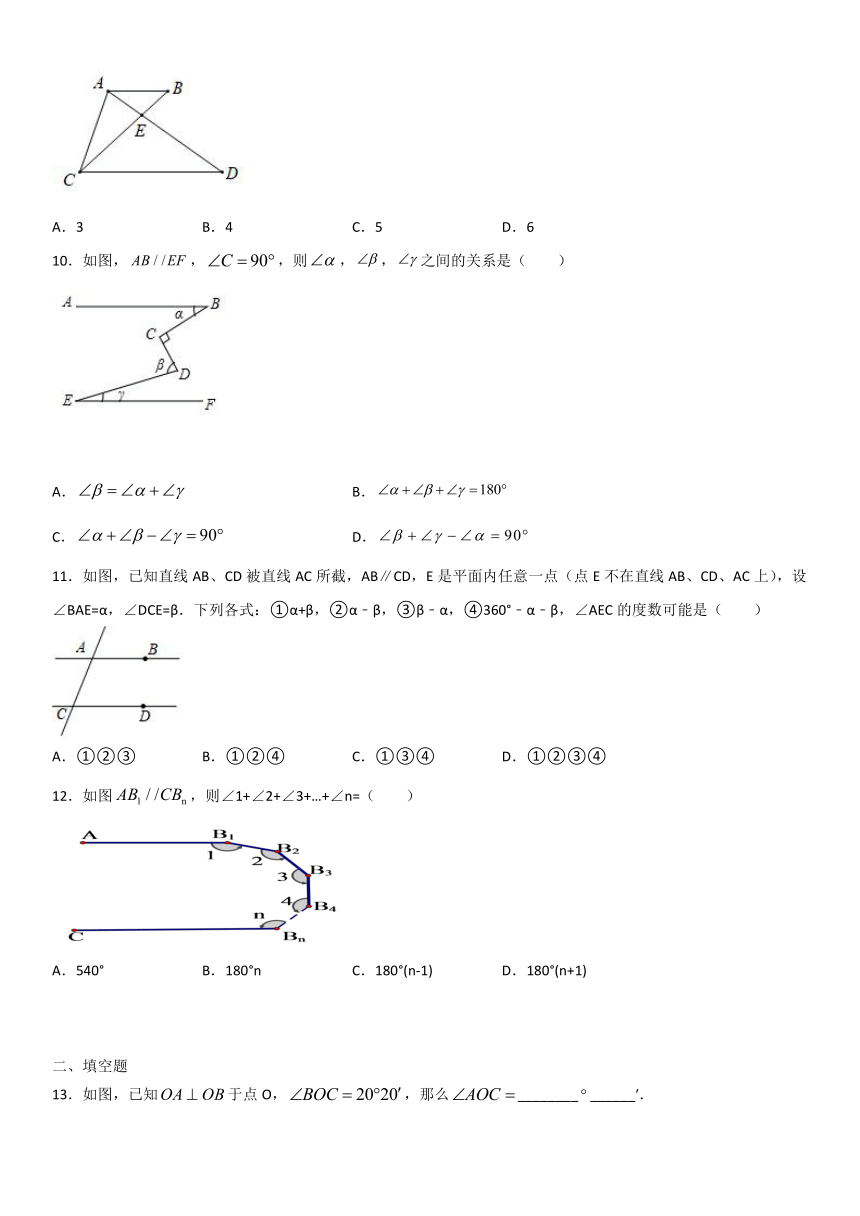
10.如图,,,则,,之间的关系是( )
A. B.
C. D.
11.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
12.如图,则∠1+∠2+∠3+…+∠n=( )
A.540° B.180°n C.180°(n-1) D.180°(n+1)
二、填空题
13.如图,已知于点O,,那么______________′.
14.点为线段上一点,不与点、重合,于点,若,则的度数为____________.
15.如图,,平分,平分,交于点F,则的度数为_________°.
16.如图,与是同位角的是__________.
17.如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°,则∠DOF的度数为__.
18.已知与(,都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且,则的度数为_________.
19.一副三角尺按如图所示叠放在一起,其中点重合,若固定三角形,将三角形绕点顺时针旋转一周,共有 _________次 出现三角形的一边与三角形AOB的某一边平行.
三、解答题
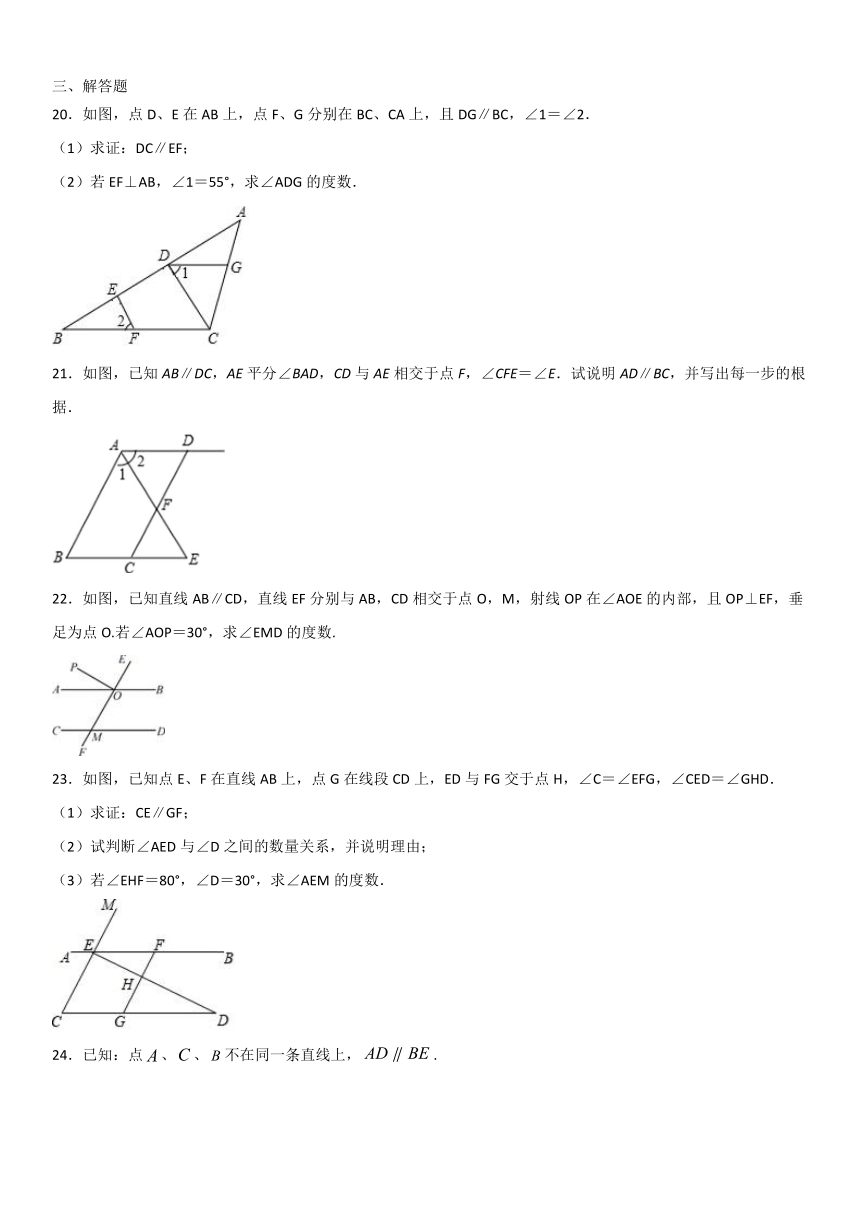
20.如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.
(1)求证:DC∥EF;
(2)若EF⊥AB,∠1=55°,求∠ADG的度数.
21.如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
22.如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
24.已知:点、、不在同一条直线上,.
(1)如图1,当,时,求的度数;
(2)如图2,、分别为、的平分线所在直线,试探究与的数量关系;
(3)如图3,在(2)的前提下,有,,直接写出的值.
25.如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.
26.如图①,已知直线PQ∥MN,点A在直线PQ上,点C,D在直线MN上,连接AC,AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.
(1)求∠AEC的度数;
(2)若将图①中的线段AD沿MN向右平移到A1D1如图②所示位置,此时A1E平分∠AA1D1,
CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数;
(3)若将图①中的线段AD沿MN向左平移到A1D1如图③所示位置,其他条件与(2)相同,求此时∠A1EC的度数(直接写出结果).
参考答案
1.B
(1)如果互余的两个角的度数之比为,则这两个角分别为,故(1)错误;
(2)根据等角的补角相等,故(2)错误;
(3),
与互余,
故(3)正确;
(4)设一个角为x,则它的余角为,它的补角为,
故(4)正确,
故正确的有(3)(4),共2个,
2.A
解:
故(1)可判定;
故(2)可判定;
,不能判定故(3)不能判定;
,不能判定故(4)不能判定.
3.B
解:∵,
∴,
∵平分,
∴,
∵,
∴,
4.D
根据直尺和圆规作∠HDG=∠AOB的过程,可知:
弧①是以M为圆心,以EF为半径画弧得到的.
故选D.
5.B
从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是PB,
6.D
如图,过点E作,
,
,
又,
,
,
,
7.D
如下图
选项A中,,
∴与不相等,故选项A错误;
如下图
选项B中,,
∵
∴与不相等,故选项B错误;
如下图
选项C中,,
∴与不相等,故选项C错误;
如下图:
选项D中,,
∴与相等;
8.B
∵∠1=∠3,∠2=∠4,
又∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=∠3+∠4=∠1+∠4=90°,
∴∠EFD=∠1+∠2=90°,
∴EC⊥FD,故③正确;
∵AB∥CD,
∴∠1=∠C,
∴∠FGD=∠4+∠C=∠4+∠1=90°,
∴FG⊥CD,故②正确;
∵∠1不一定等于∠2,
∴∠C≠∠D,故①不正确.
故选:B.
9.B
∵
∴与的高相等
∵
∴
设的面积为,则,
∴
解得
∴
10.C
如图,分别过C、D作AB的平行线CM和DN,
∵,
∴,
∴,,,
∴,
又∵,
∴,
∴,
即,
11.D
E点有4中情况,分四种情况讨论如下:
由AB∥CD,可得∠AOC=∠DCE1=β
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α
过点E2作AB的平行线,由AB∥CD,
可得∠1=∠BAE2=α,∠2=∠DCE2=β
∴∠AE2C=α+β
由AB∥CD,可得∠BOE3=∠DCE3=β
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α-β
由AB∥CD,可得
∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°-α-β
∴∠AEC的度数可能是①α+β,②α﹣β,③β-α,④360°﹣α﹣β,故选D.
12.C
解:根据题意,作,,,
∵,
∴,,,……
∴,……
∴;
13.69 40
解:如右图所示,
∵OA⊥OB,
∴∠AOB=90°,
∴∠AOC=∠AOB-∠BOC=90°-20°20′=69°40′.
14.或
解:如图,当OC,OD在线段AB的同侧时,
,
,
,
,
∵,
∴,
当OC,OD在线段AB的异侧时,反向延长OD到E,
,
,
,
,
∵,
∴,
,
综上,或;
故答案为:或
15.16
解:∵∠BCA=64°,CE平分∠ACB,
∴∠BCF=32°,
∵CD平分∠ECB,
∴∠BCD=∠DCF=16°,
∵DF∥BC,
∴∠CDF=∠BCD=16°,
16.①②
解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.
故答案为:①②.
17.
解:∵EO⊥CD于点O,
∴∠COE=90°,
∵∠BOE=50°,
∴∠COB=90°+50°=140°,
∴∠AOD=140°,
∵OF平分∠AOD,
∴∠FOD=∠AOD=70°,
18.或.
①如图1,作EF∥BD,
∴∠B=∠BEF,
∵EF∥BD,BD∥AC,
∴EF∥AC,
∴∠A=∠AEF,
∴∠A+∠B=∠AEF+∠BEF=,
∵,
∴∠A=;
②如图2,作EF∥BD,
∴∠B+∠BEF=,
∵EF∥BD,BD∥AC,
∴EF∥AC,
∴∠A+∠AEF=,
∴∠A+∠AEB+∠B=,
∵∠AEB=∠AEF+∠BEF=,
∴∠A+∠B=,
∵,
∴∠A=;
故答案为:或.
.
19.
解:分8种情况讨论:
(1)如图1,AD边与OB边平行时,∠BAD=45°;
(2)如图2,当AC边与OB平行时,∠BAD=90°+45°=135°;
(3)如图3,DC边与AB边平行时,∠BAD=60°+90°=150°,
(4)如图4,DC边与OB边平行时,∠BAD=135°+30°=165°,
(5)如图5,DC边与OB边平行时,∠BAD=45°﹣30°=15°;
(6)如图6,DC边与AO边平行时,∠BAD=15°+90°=105°
(7)如图7,DC边与AB边平行时,∠BAD=30°,
(8)如图8,DC边与AO边平行时,∠BAD=30°+45°=75°;
综上所述:∠BAD的所有可能的值为:15°,30°,45°,75°,105°,135°,150°,165°.
故答案为:8.
20.
∵
∴∠1=∠DCF,
∵
∴∠2=∠DCF,
∴;
(2)∵,∴∠BEF=90°,
∴∠B=90°-∠2=35°,
又∵
∴=∠B=35°.
21.
证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∴∠CFE=∠2(等量代换)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
22.60°
试题分析:由OP⊥EF,∠AOP=30°,求出∠EOB=180°-30°-90°=60°.再根据AB∥CD,得出∠EMD=∠EOB=60°.
试题解析:∵OP⊥EF,
所以∠EOP=90°.
又因为∠EOB+∠POE+∠AOP=180°,
所以∠EOB=180°-∠AOP-∠POE.
因为∠AOP=30°,所以∠EOB=180°-30°-90°=60°.
因为AB∥CD,
所以∠EMD=∠EOB=60°.
23.
(1)∵∠CED=∠GHD,
∴CB∥GF;
(2)∠AED+∠D=180°;
理由:∵CB∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=80°+30°=110°,
又∵CE∥GF,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
24.
(1)在图①中,过点C作CF∥AD,则CF∥BE.
∵CF∥AD∥BE,
∴∠ACF=∠A,∠BCF=180°﹣∠B,
∴∠ACB=∠ACF+∠BCF=180°﹣(∠B﹣∠A)=120°.
(2)在图2中,过点Q作QM∥AD,则QM∥BE.
∵QM∥AD,QM∥BE,
∴∠AQM=∠NAD,∠BQM=∠EBQ.
∵AQ平分∠CAD,BQ平分∠CBE,
∴∠NAD=∠CAD,∠EBQ=∠CBE,
∴∠AQB=∠BQM﹣∠AQM=(∠CBE﹣∠CAD).
∵∠C=180°﹣(∠CBE﹣∠CAD)=180°﹣2∠AQB,
∴2∠AQB+∠C=180°.
(3)∵AC∥QB,
∴∠AQB=∠CAP=∠CAD,∠ACP=∠PBQ=∠CBE,
∴∠ACB=180°﹣∠ACP=180°﹣∠CBE.
∵2∠AQB+∠ACB=180°,
∴∠CAD=∠CBE.
又∵QP⊥PB,
∴∠CAP+∠ACP=90°,即∠CAD+∠CBE=180°,
∴∠CAD=60°,∠CBE=120°,
∴∠ACB=180°﹣(∠CBE﹣∠CAD)=120°,
∴∠DAC:∠ACB:∠CBE=60°:120°:120°=1:2:2.
25.
(1)∵PM∥AB,α=20°,
∴∠EPM=∠AEP=20°,
∵AB∥CD,PM∥AB,
∴PM∥CD,
∴∠MPF=∠CFP=50°,
∴∠EPF=20°+50°=70°,
故答案为20,70;
(2)∵PE平分∠AEH,
∴∠AEH=2α=40°,
∵AD∥BC,
∴∠END=∠AEH=40°,
又∵FG平分∠DFI,
∴∠IFG=∠DFG=β=50°,
∴∠CFI=180°-2β=80°;
(3)由(2)可得,∠CFI=180°-2β,
∵AB∥CD,
∴∠END=∠AEN=2α,
∴当FI∥EH时,∠END=∠CFI,
即2α=180°-2β,
∴α+β=90°.
26.
【详解】解:(1)如图1所示:
∵直线PQ∥MN,∠ADC=30°,
∴∠ADC=∠QAD=30°,
∴∠PAD=150°,
∵∠PAC=50°,AE平分∠PAD,
∴∠PAE=75°,
∴∠CAE=25°,
可得∠PAC=∠ACN=50°,
∵CE平分∠ACD,
∴∠ECA=25°,
∴∠AEC=180°﹣25°﹣25°=130°;
(2)如图2所示:
∵∠A1D1C=30°,线段AD沿MN向右平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∴∠PA1D1=150°,
∵A1E平分∠AA1D1,
∴∠PA1E=∠EA1D1=75°,
∵∠PAC=50°,PQ∥MN,
∴∠CAQ=130°,∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=25°,
∴∠CEA1=360°﹣25°﹣130°﹣75°=130°;
(3)如图3所示:
过点E作FE∥PQ,
∵∠A1D1C=30°,线段AD沿MN向左平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∵A1E平分∠AA1D1,
∴∠QA1E=∠2=15°,
∵∠PAC=50°,PQ∥MN,
∴∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=∠ECN=∠1=25°,
∴∠CEA1=∠1+∠2=15°+25°=40°.
一、单选题
1.下列说法正确的是( )
(1)如果互余的两个角的度数之比为,那么这两个角分别为和
(2)如果两个角是同一个角的补角,那么这两个角不一定相等
(3)如果两个角的度数分别是和,那么这两个角互余
(4)一个锐角的余角比这个锐角的补角小
A.个 B.个 C.个 D.个
2.如图,直线a,b被直线c所截,现给出下列四个条件:(1);(2);(3);(4),其中能判定的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
3.如图,已知直线,平分交直线于点,若,则等于( )
A.25° B.29° C.30° D.45°
4.用直尺和圆规作∠HDG=∠AOB的过程,弧①是( )
A.以D为圆心,以DN为半径画弧
B.以D为圆心,以EF为半径画弧
C.以M为圆心,以DN为半径画弧
D.以M为圆心,以EF为半径画弧
5.如图,从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的是( )
A.PA B.PB C.PC D.PD
6.如图,,,,则( )
A. B. C. D.
7.将一副直角三角尺按如图所示的不同方式摆放,则图中与相等的是( ).
A. B. C. D.
8.如图,,分别交于点,链接,点G是线段CD上的点,连接FG,若,,则结论①,②,③,正确的是( )
A.①② B.②③ C.①③ D.①②③
9.已知,,且,和的面积分别为2和8,则的面积是( )
A.3 B.4 C.5 D.6
10.如图,,,则,,之间的关系是( )
A. B.
C. D.
11.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
12.如图,则∠1+∠2+∠3+…+∠n=( )
A.540° B.180°n C.180°(n-1) D.180°(n+1)
二、填空题
13.如图,已知于点O,,那么______________′.
14.点为线段上一点,不与点、重合,于点,若,则的度数为____________.
15.如图,,平分,平分,交于点F,则的度数为_________°.
16.如图,与是同位角的是__________.
17.如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°,则∠DOF的度数为__.
18.已知与(,都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且,则的度数为_________.
19.一副三角尺按如图所示叠放在一起,其中点重合,若固定三角形,将三角形绕点顺时针旋转一周,共有 _________次 出现三角形的一边与三角形AOB的某一边平行.
三、解答题
20.如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.
(1)求证:DC∥EF;
(2)若EF⊥AB,∠1=55°,求∠ADG的度数.
21.如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
22.如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
23.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
24.已知:点、、不在同一条直线上,.
(1)如图1,当,时,求的度数;
(2)如图2,、分别为、的平分线所在直线,试探究与的数量关系;
(3)如图3,在(2)的前提下,有,,直接写出的值.
25.如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.
26.如图①,已知直线PQ∥MN,点A在直线PQ上,点C,D在直线MN上,连接AC,AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.
(1)求∠AEC的度数;
(2)若将图①中的线段AD沿MN向右平移到A1D1如图②所示位置,此时A1E平分∠AA1D1,
CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数;
(3)若将图①中的线段AD沿MN向左平移到A1D1如图③所示位置,其他条件与(2)相同,求此时∠A1EC的度数(直接写出结果).
参考答案
1.B
(1)如果互余的两个角的度数之比为,则这两个角分别为,故(1)错误;
(2)根据等角的补角相等,故(2)错误;
(3),
与互余,
故(3)正确;
(4)设一个角为x,则它的余角为,它的补角为,
故(4)正确,
故正确的有(3)(4),共2个,
2.A
解:
故(1)可判定;
故(2)可判定;
,不能判定故(3)不能判定;
,不能判定故(4)不能判定.
3.B
解:∵,
∴,
∵平分,
∴,
∵,
∴,
4.D
根据直尺和圆规作∠HDG=∠AOB的过程,可知:
弧①是以M为圆心,以EF为半径画弧得到的.
故选D.
5.B
从直线EF外一点P向EF引四条线段PA,PB,PC,PD,其中最短的一条是PB,
6.D
如图,过点E作,
,
,
又,
,
,
,
7.D
如下图
选项A中,,
∴与不相等,故选项A错误;
如下图
选项B中,,
∵
∴与不相等,故选项B错误;
如下图
选项C中,,
∴与不相等,故选项C错误;
如下图:
选项D中,,
∴与相等;
8.B
∵∠1=∠3,∠2=∠4,
又∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=∠3+∠4=∠1+∠4=90°,
∴∠EFD=∠1+∠2=90°,
∴EC⊥FD,故③正确;
∵AB∥CD,
∴∠1=∠C,
∴∠FGD=∠4+∠C=∠4+∠1=90°,
∴FG⊥CD,故②正确;
∵∠1不一定等于∠2,
∴∠C≠∠D,故①不正确.
故选:B.
9.B
∵
∴与的高相等
∵
∴
设的面积为,则,
∴
解得
∴
10.C
如图,分别过C、D作AB的平行线CM和DN,
∵,
∴,
∴,,,
∴,
又∵,
∴,
∴,
即,
11.D
E点有4中情况,分四种情况讨论如下:
由AB∥CD,可得∠AOC=∠DCE1=β
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α
过点E2作AB的平行线,由AB∥CD,
可得∠1=∠BAE2=α,∠2=∠DCE2=β
∴∠AE2C=α+β
由AB∥CD,可得∠BOE3=∠DCE3=β
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α-β
由AB∥CD,可得
∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°-α-β
∴∠AEC的度数可能是①α+β,②α﹣β,③β-α,④360°﹣α﹣β,故选D.
12.C
解:根据题意,作,,,
∵,
∴,,,……
∴,……
∴;
13.69 40
解:如右图所示,
∵OA⊥OB,
∴∠AOB=90°,
∴∠AOC=∠AOB-∠BOC=90°-20°20′=69°40′.
14.或
解:如图,当OC,OD在线段AB的同侧时,
,
,
,
,
∵,
∴,
当OC,OD在线段AB的异侧时,反向延长OD到E,
,
,
,
,
∵,
∴,
,
综上,或;
故答案为:或
15.16
解:∵∠BCA=64°,CE平分∠ACB,
∴∠BCF=32°,
∵CD平分∠ECB,
∴∠BCD=∠DCF=16°,
∵DF∥BC,
∴∠CDF=∠BCD=16°,
16.①②
解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.
故答案为:①②.
17.
解:∵EO⊥CD于点O,
∴∠COE=90°,
∵∠BOE=50°,
∴∠COB=90°+50°=140°,
∴∠AOD=140°,
∵OF平分∠AOD,
∴∠FOD=∠AOD=70°,
18.或.
①如图1,作EF∥BD,
∴∠B=∠BEF,
∵EF∥BD,BD∥AC,
∴EF∥AC,
∴∠A=∠AEF,
∴∠A+∠B=∠AEF+∠BEF=,
∵,
∴∠A=;
②如图2,作EF∥BD,
∴∠B+∠BEF=,
∵EF∥BD,BD∥AC,
∴EF∥AC,
∴∠A+∠AEF=,
∴∠A+∠AEB+∠B=,
∵∠AEB=∠AEF+∠BEF=,
∴∠A+∠B=,
∵,
∴∠A=;
故答案为:或.
.
19.
解:分8种情况讨论:
(1)如图1,AD边与OB边平行时,∠BAD=45°;
(2)如图2,当AC边与OB平行时,∠BAD=90°+45°=135°;
(3)如图3,DC边与AB边平行时,∠BAD=60°+90°=150°,
(4)如图4,DC边与OB边平行时,∠BAD=135°+30°=165°,
(5)如图5,DC边与OB边平行时,∠BAD=45°﹣30°=15°;
(6)如图6,DC边与AO边平行时,∠BAD=15°+90°=105°
(7)如图7,DC边与AB边平行时,∠BAD=30°,
(8)如图8,DC边与AO边平行时,∠BAD=30°+45°=75°;
综上所述:∠BAD的所有可能的值为:15°,30°,45°,75°,105°,135°,150°,165°.
故答案为:8.
20.
∵
∴∠1=∠DCF,
∵
∴∠2=∠DCF,
∴;
(2)∵,∴∠BEF=90°,
∴∠B=90°-∠2=35°,
又∵
∴=∠B=35°.
21.
证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∴∠CFE=∠2(等量代换)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
22.60°
试题分析:由OP⊥EF,∠AOP=30°,求出∠EOB=180°-30°-90°=60°.再根据AB∥CD,得出∠EMD=∠EOB=60°.
试题解析:∵OP⊥EF,
所以∠EOP=90°.
又因为∠EOB+∠POE+∠AOP=180°,
所以∠EOB=180°-∠AOP-∠POE.
因为∠AOP=30°,所以∠EOB=180°-30°-90°=60°.
因为AB∥CD,
所以∠EMD=∠EOB=60°.
23.
(1)∵∠CED=∠GHD,
∴CB∥GF;
(2)∠AED+∠D=180°;
理由:∵CB∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=80°+30°=110°,
又∵CE∥GF,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
24.
(1)在图①中,过点C作CF∥AD,则CF∥BE.
∵CF∥AD∥BE,
∴∠ACF=∠A,∠BCF=180°﹣∠B,
∴∠ACB=∠ACF+∠BCF=180°﹣(∠B﹣∠A)=120°.
(2)在图2中,过点Q作QM∥AD,则QM∥BE.
∵QM∥AD,QM∥BE,
∴∠AQM=∠NAD,∠BQM=∠EBQ.
∵AQ平分∠CAD,BQ平分∠CBE,
∴∠NAD=∠CAD,∠EBQ=∠CBE,
∴∠AQB=∠BQM﹣∠AQM=(∠CBE﹣∠CAD).
∵∠C=180°﹣(∠CBE﹣∠CAD)=180°﹣2∠AQB,
∴2∠AQB+∠C=180°.
(3)∵AC∥QB,
∴∠AQB=∠CAP=∠CAD,∠ACP=∠PBQ=∠CBE,
∴∠ACB=180°﹣∠ACP=180°﹣∠CBE.
∵2∠AQB+∠ACB=180°,
∴∠CAD=∠CBE.
又∵QP⊥PB,
∴∠CAP+∠ACP=90°,即∠CAD+∠CBE=180°,
∴∠CAD=60°,∠CBE=120°,
∴∠ACB=180°﹣(∠CBE﹣∠CAD)=120°,
∴∠DAC:∠ACB:∠CBE=60°:120°:120°=1:2:2.
25.
(1)∵PM∥AB,α=20°,
∴∠EPM=∠AEP=20°,
∵AB∥CD,PM∥AB,
∴PM∥CD,
∴∠MPF=∠CFP=50°,
∴∠EPF=20°+50°=70°,
故答案为20,70;
(2)∵PE平分∠AEH,
∴∠AEH=2α=40°,
∵AD∥BC,
∴∠END=∠AEH=40°,
又∵FG平分∠DFI,
∴∠IFG=∠DFG=β=50°,
∴∠CFI=180°-2β=80°;
(3)由(2)可得,∠CFI=180°-2β,
∵AB∥CD,
∴∠END=∠AEN=2α,
∴当FI∥EH时,∠END=∠CFI,
即2α=180°-2β,
∴α+β=90°.
26.
【详解】解:(1)如图1所示:
∵直线PQ∥MN,∠ADC=30°,
∴∠ADC=∠QAD=30°,
∴∠PAD=150°,
∵∠PAC=50°,AE平分∠PAD,
∴∠PAE=75°,
∴∠CAE=25°,
可得∠PAC=∠ACN=50°,
∵CE平分∠ACD,
∴∠ECA=25°,
∴∠AEC=180°﹣25°﹣25°=130°;
(2)如图2所示:
∵∠A1D1C=30°,线段AD沿MN向右平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∴∠PA1D1=150°,
∵A1E平分∠AA1D1,
∴∠PA1E=∠EA1D1=75°,
∵∠PAC=50°,PQ∥MN,
∴∠CAQ=130°,∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=25°,
∴∠CEA1=360°﹣25°﹣130°﹣75°=130°;
(3)如图3所示:
过点E作FE∥PQ,
∵∠A1D1C=30°,线段AD沿MN向左平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∵A1E平分∠AA1D1,
∴∠QA1E=∠2=15°,
∵∠PAC=50°,PQ∥MN,
∴∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=∠ECN=∠1=25°,
∴∠CEA1=∠1+∠2=15°+25°=40°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
