沪科版初中数学八年级下册 16.1二次根式 课件 (1)(17张)
文档属性
| 名称 | 沪科版初中数学八年级下册 16.1二次根式 课件 (1)(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 15:12:15 | ||
图片预览






文档简介
二次根式
温故知新
1.什么叫平方根、算术平方根?请举例说明。
2.用数学式子表示:
(1)求下列各数的算术平方根:
25, , 6
(2)面积为m的正方形的边长为多少?
3.这些式子有什么共同特点?
1、二次根式的概念:
形如 的式子叫做二次根式。
2、思考:
3.你觉得一个二次根式需要满足几个条件?
( 双重非负性)
1、当a≥0时, 表示a的算术平方根,
当a<0时, 没有意义。
2、 a可以是数,也可以是式.
3、形式上含有二次根号
4、既可表示开方运算,也可表示运算
的结果.
二次根式 的认识
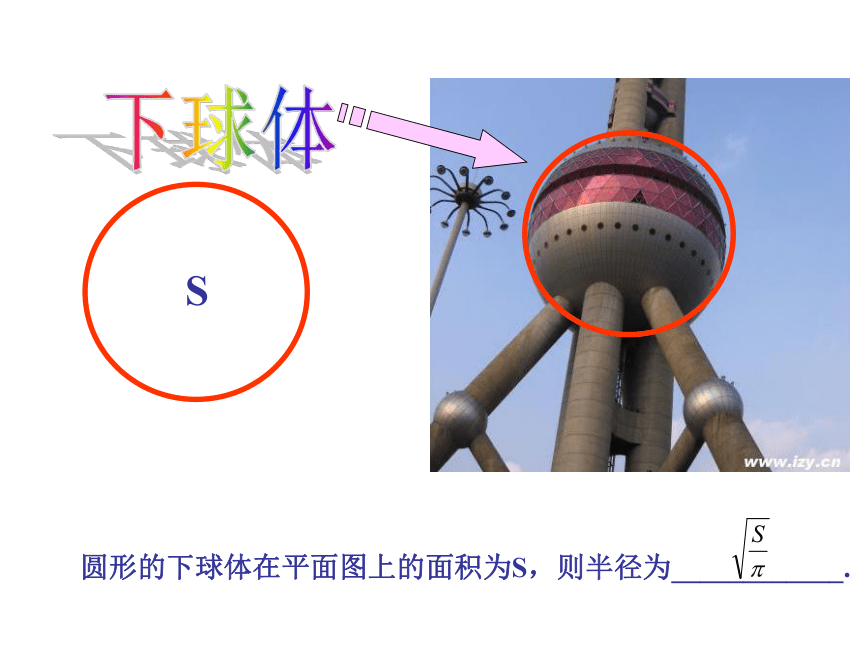
下球体
S
圆形的下球体在平面图上的面积为S,则半径为____________.
小结:
2.怎样判断一个式子是不是二次根式?
3.如何确定二次根式中字母的取值范围?
(1)形式上含有二次根号
(2)被开方数a为非负数,
分母不为0
被开方数大于或等于0
结合数轴,写出解集来
1.怎样的式子叫二次根式?
( 双重非负性)
2、性质探索:
性质1
是2的算术平方根,则
是7的算术平方根,则
是13的算术平方根,则
1.求下列各式的值:
巩固练习:
2.把下列正数写成一个数的平方形式:
(1)9 (2)0.25 (3)3 (4)2.5
2、性质探索:
基础训练
1计算下列各式的值:
( )2 ( )2 ( )2 ( )2
2在实数范围内分解下列因式:
(1)x2-3 (2)x4-4 (3) 2x2-3
3填空:(1) - =_________.
(2) =
(3)a、b、c为三角形的三条边,则
=_____
4已知2<x<3,化简:
1.求下列各式的值:
巩固练习:
问题解答:
4.二次根式有意义的条件
—— 被开方数整体大于或等于零
1. 是二次根式吗?
2.假设 ,这个式子会变得怎样?
3. 为何值时, 在实数范围内有意义?
例题讲解
例1: 为何值时,下列式子在实数范围内有意义?
3、在实数范围内分解因式:
4、已知:
求 的值。
本节课你有哪些收获?谈谈你的感受。
温故知新
1.什么叫平方根、算术平方根?请举例说明。
2.用数学式子表示:
(1)求下列各数的算术平方根:
25, , 6
(2)面积为m的正方形的边长为多少?
3.这些式子有什么共同特点?
1、二次根式的概念:
形如 的式子叫做二次根式。
2、思考:
3.你觉得一个二次根式需要满足几个条件?
( 双重非负性)
1、当a≥0时, 表示a的算术平方根,
当a<0时, 没有意义。
2、 a可以是数,也可以是式.
3、形式上含有二次根号
4、既可表示开方运算,也可表示运算
的结果.
二次根式 的认识
下球体
S
圆形的下球体在平面图上的面积为S,则半径为____________.
小结:
2.怎样判断一个式子是不是二次根式?
3.如何确定二次根式中字母的取值范围?
(1)形式上含有二次根号
(2)被开方数a为非负数,
分母不为0
被开方数大于或等于0
结合数轴,写出解集来
1.怎样的式子叫二次根式?
( 双重非负性)
2、性质探索:
性质1
是2的算术平方根,则
是7的算术平方根,则
是13的算术平方根,则
1.求下列各式的值:
巩固练习:
2.把下列正数写成一个数的平方形式:
(1)9 (2)0.25 (3)3 (4)2.5
2、性质探索:
基础训练
1计算下列各式的值:
( )2 ( )2 ( )2 ( )2
2在实数范围内分解下列因式:
(1)x2-3 (2)x4-4 (3) 2x2-3
3填空:(1) - =_________.
(2) =
(3)a、b、c为三角形的三条边,则
=_____
4已知2<x<3,化简:
1.求下列各式的值:
巩固练习:
问题解答:
4.二次根式有意义的条件
—— 被开方数整体大于或等于零
1. 是二次根式吗?
2.假设 ,这个式子会变得怎样?
3. 为何值时, 在实数范围内有意义?
例题讲解
例1: 为何值时,下列式子在实数范围内有意义?
3、在实数范围内分解因式:
4、已知:
求 的值。
本节课你有哪些收获?谈谈你的感受。
