四川省成都第七高级中学2020-2021学年高一上学期1月阶段性测试数学试题 Word版含答案
文档属性
| 名称 | 四川省成都第七高级中学2020-2021学年高一上学期1月阶段性测试数学试题 Word版含答案 | 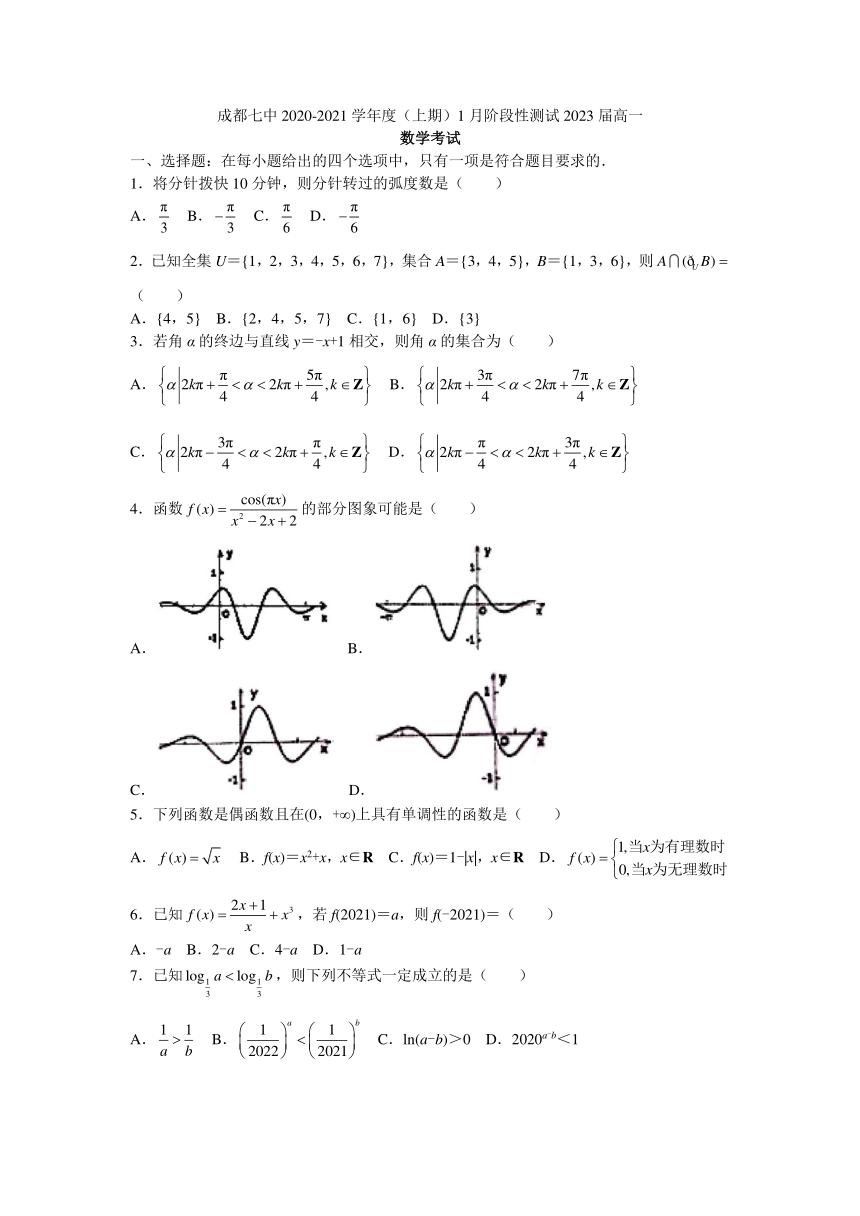 | |
| 格式 | doc | ||
| 文件大小 | 554.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 11:38:32 | ||
图片预览



文档简介
成都七中2020-2021学年度(上期)1月阶段性测试2023届高一
数学考试
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.将分针拨快10分钟,则分针转过的弧度数是( )
A. B. C. D.
2.已知全集U={1,2,3,4,5,6,7},集合A={3,4,5},B={1,3,6},则( )
A.{4,5} B.{2,4,5,7} C.{1,6} D.{3}
3.若角α的终边与直线y=-x+1相交,则角α的集合为( )
A. B.
C. D.
4.函数的部分图象可能是( )
A. B.
C. D.
5.下列函数是偶函数且在(0,+∞)上具有单调性的函数是( )
A. B.f(x)=x2+x,x∈R C.f(x)=1-|x|,x∈R D.
6.已知,若f(2021)=a,则f(-2021)=( )
A.-a B.2-a C.4-a D.1-a
7.已知,则下列不等式一定成立的是( )
A. B. C.ln(a-b)>0 D.2020a-b<1
8.已知2lg(x-2y)=lg x+lg y,则的值为( )
A.1 B.4 C.1或4 D.或4
9.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”如下:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数.例如[-2.6]=-3,[2.3]=2,已知函数,若函数y=f[(x)]的值域集合为Q,则下列集合不是Q的子集的是( )
A.[0,+∞) B.{0,2} C.{1,2} D.{1,2,3}
10.关于函数f(x)=sin|x|+|sin x|有下述四个结论:①f(x)是偶函数;②f(x)在区间单调递增;③f(x)在[-π,π]有4个零点;④f(x)的最大值为2
其中所有正确结论的编号是( )
A.①②④ B.②④ C.①④ D.①③
11.“喊泉”是一种地下水的毛细现象,人们在泉口吼叫或发出其他声音时,声波传入泉洞内的储水池,进而产生“共鸣”等物理声学作用,激起水波,形成涌泉.声音越大,涌起的泉水越高.已知听到的声强m与标准声调m0(m0约为10-12,单位:W/m2)之比的常用对数称作声强的声强级,记作L(贝尔),即,取贝尔的10倍作为响度的常用单位,简称为分贝.已知某处“喊泉”的声音响度y(分贝)与喷出的泉水高度x(米)满足关系式y=2x,现知A同学大喝一声激起的涌泉最高高度为50米,若A同学大喝一声的声强大约相当于10个B同学同时大喝一声的声强,则B同学大喝一声激起的涌泉最高高度约为( )米
A.5 B.10 C.45 D.48
12.已知函数,若函数y=f(x)-a恰有5个零点x1,x2,x3,x4,x5,且x1<x2<x3<x4<x5,a为实数,则的取值范围为( )
A. B. C. D.
二、填空题
13.函数在[-2,-1]上的值域是________.
14.已知函数,则f(f(-3))=________.
15.若函数f(x)=msin 2x+3cos 2x的图象关于直线对称,则实数m=________.
16.设函数(a∈R,e为自然对数的底数),若曲线y=cos x上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.设集合A={x|x2-x-2≤0},集合B={x|2m<x<1},且B≠?.
(1)若A∩B=B,求实数m的取值范围;
(2)若中只有一个整数,求实数m的取值范围.
18.已知函数,a,b∈R,a≠0,b≠0,,且方程f(x)=x有且仅有一个实数解;
(1)求a、b的值;
(2)当时,不等式(x+1)·f(x)>m(m-x)-1恒成立,求实数m的范围.
19.已知函数部分图象如图所示.
(1)求函数f(x)的解析式,并求出f(x)的单调递增区间;
(2)将函数f(x)的图象上各个点的横坐标变为原来的2倍,再将图象向右平移个单位,得到g(x)的图象,若存在使得等式2a=-2g2(x)+3g(x)+1成立,求实数a的取值范围.
20.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x
y -1 1 3 1 -1 1 3
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为,当时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
21.2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为200万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,(万元).当年产量不小于80千件时,(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
22.已知函数.
(1)直接写出h(x)在上的单调区间(无需证明);
(2)求h(x)在上的最大值;
(3)设函数f(x)的定义域为I,若存在区间A?I,满足:?x1∈A,,使得f(x1)=f(x2),则称区间A为f(x)的“Г区间”.已知,若是函数f(x)的“Г区间”,求实数b的最大值.
成都七中2020-2021学年度(上期)1月阶段性测试2023届高一
参考答案
一、选择题:1-5 BADAC 6-10 CBBAC 11-12 CD
二、填空题:13.[2,6] 14.0 15.-3 16.[1,e+2]
三、解答题:
17.解:(1)由x2-x-2≤0,得-1≤x≤2,则A={x|-1≤x≤2}. 因为A∩B=B,所以B?A, 又B={x|2m<x<1},且B≠?.则, 所以,m的取值范围是.
(2)∵A={x|-1≤x≤2},∴, 又B={x|2m<x<1},且B≠?. 若中只有一个整数,则-3≤2m<-2,得; 所以,m的取值范围是.
18.解:(1)∵,且;∴,即a+b=2; 又只有一个实数解;∴有且仅有一个实数解为0;∴b=1,a=1;∴
.
(2)∴;∴x+1>0;∴(x+1)f(x)>m(m-x)-1恒成立?(1+m)x>m2-1; 当m+1>0时,即m>-1时,有m-1<x恒成立?m<x+1?m<(x+1)min,∴; 当m+1<0,即m<-1时,同理可得;∴此时m不存在. 综上,m的取值范围是.
19.(1)由图象可知:,所以T=π,则, 又,k∈Z得,又,所以, 所以, 由
,k∈Z得,,k∈Z, 所以f(x)的单调递增区间为;
(2)由图象变换得g(x)=sin x,所以存在使得等式2a=-2sin2x+3sin x+1成立, 即2a=-2sin2x+3sin x+1在上有解, 令t=sin x∈[0,1],则
, 所以,即.
20.解:(1)绘制函数图象如图所示:
设f(x)的最小正周期为T,得.由得ω=1. 又解得, 令,即,k∈Z, 据此可得:,又,令k=0可得. 所以函数的解析式为.
(2)因为函数的周期为, 又k>0,所以k=3. 令,因为,所以. sin t=s在上有两个不同的解,等价于函数y=sin t与y=s的图象有两个不同的交点,∴, 所以方程f(kx)=m在时恰好有两个不同的解的条件是, 即实数m的取值范围是.
21.解:(1)因为每件商品售价为0.05万元,则x千件商品销售额为0.05×1000x万元, 依题意得:当0<x<80时,, 当x≥80时,, 所以
;
(2)当0<x<80时,, 此时,当x=30时,即L(x)≤L(30)=250万元. 当x≥80时,, 此时,x=100,即L(x)≤L(100)=200万元, 由于250>200, 所以当年产量为30千件时,该厂在这一商品生产中所获利润最大,最大利润为250万元
22.(1)h(x)在上单调递减,在[1,2]上单调递增;
(2)由题意知,, ①若,则h(x)在上单调递减,所以h(x)的最大值为 ②若1<a≤2,则h(x)在上单调递减,在[1,a]上单调递增,此时, 所以h(x)的最大值为; ③若a>2,则h(x)在上单调递减,在[1,a]上单调递增,此时, 所以h(x)的最大值为
综上知:若,则h(x)的最大值为;若a>2,则h(x)的最大值为.
(3)由(1)(2)知: ①当时,f(x)在上的值域为,f(x)在[b,2]上的值域为,∵,有,满足,?x2∈[b,2],使得f(x1)=f(x2),∴此时是f(x)的“Г区间”, ②当1<b≤2时,f(x)在上的值域为,f(x)在[b,2]上的值域为,∵当x1∈[1,b)时,,∴?x1∈[1,b),使得,即?x1∈[1,b),?x2∈[b,2],f(x1)≠f(x2)∴此时不是f(x)的“Г区间”, 综上,实数b的最大值为1.
数学考试
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.将分针拨快10分钟,则分针转过的弧度数是( )
A. B. C. D.
2.已知全集U={1,2,3,4,5,6,7},集合A={3,4,5},B={1,3,6},则( )
A.{4,5} B.{2,4,5,7} C.{1,6} D.{3}
3.若角α的终边与直线y=-x+1相交,则角α的集合为( )
A. B.
C. D.
4.函数的部分图象可能是( )
A. B.
C. D.
5.下列函数是偶函数且在(0,+∞)上具有单调性的函数是( )
A. B.f(x)=x2+x,x∈R C.f(x)=1-|x|,x∈R D.
6.已知,若f(2021)=a,则f(-2021)=( )
A.-a B.2-a C.4-a D.1-a
7.已知,则下列不等式一定成立的是( )
A. B. C.ln(a-b)>0 D.2020a-b<1
8.已知2lg(x-2y)=lg x+lg y,则的值为( )
A.1 B.4 C.1或4 D.或4
9.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”如下:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数.例如[-2.6]=-3,[2.3]=2,已知函数,若函数y=f[(x)]的值域集合为Q,则下列集合不是Q的子集的是( )
A.[0,+∞) B.{0,2} C.{1,2} D.{1,2,3}
10.关于函数f(x)=sin|x|+|sin x|有下述四个结论:①f(x)是偶函数;②f(x)在区间单调递增;③f(x)在[-π,π]有4个零点;④f(x)的最大值为2
其中所有正确结论的编号是( )
A.①②④ B.②④ C.①④ D.①③
11.“喊泉”是一种地下水的毛细现象,人们在泉口吼叫或发出其他声音时,声波传入泉洞内的储水池,进而产生“共鸣”等物理声学作用,激起水波,形成涌泉.声音越大,涌起的泉水越高.已知听到的声强m与标准声调m0(m0约为10-12,单位:W/m2)之比的常用对数称作声强的声强级,记作L(贝尔),即,取贝尔的10倍作为响度的常用单位,简称为分贝.已知某处“喊泉”的声音响度y(分贝)与喷出的泉水高度x(米)满足关系式y=2x,现知A同学大喝一声激起的涌泉最高高度为50米,若A同学大喝一声的声强大约相当于10个B同学同时大喝一声的声强,则B同学大喝一声激起的涌泉最高高度约为( )米
A.5 B.10 C.45 D.48
12.已知函数,若函数y=f(x)-a恰有5个零点x1,x2,x3,x4,x5,且x1<x2<x3<x4<x5,a为实数,则的取值范围为( )
A. B. C. D.
二、填空题
13.函数在[-2,-1]上的值域是________.
14.已知函数,则f(f(-3))=________.
15.若函数f(x)=msin 2x+3cos 2x的图象关于直线对称,则实数m=________.
16.设函数(a∈R,e为自然对数的底数),若曲线y=cos x上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.设集合A={x|x2-x-2≤0},集合B={x|2m<x<1},且B≠?.
(1)若A∩B=B,求实数m的取值范围;
(2)若中只有一个整数,求实数m的取值范围.
18.已知函数,a,b∈R,a≠0,b≠0,,且方程f(x)=x有且仅有一个实数解;
(1)求a、b的值;
(2)当时,不等式(x+1)·f(x)>m(m-x)-1恒成立,求实数m的范围.
19.已知函数部分图象如图所示.
(1)求函数f(x)的解析式,并求出f(x)的单调递增区间;
(2)将函数f(x)的图象上各个点的横坐标变为原来的2倍,再将图象向右平移个单位,得到g(x)的图象,若存在使得等式2a=-2g2(x)+3g(x)+1成立,求实数a的取值范围.
20.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x
y -1 1 3 1 -1 1 3
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为,当时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
21.2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为200万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,(万元).当年产量不小于80千件时,(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
22.已知函数.
(1)直接写出h(x)在上的单调区间(无需证明);
(2)求h(x)在上的最大值;
(3)设函数f(x)的定义域为I,若存在区间A?I,满足:?x1∈A,,使得f(x1)=f(x2),则称区间A为f(x)的“Г区间”.已知,若是函数f(x)的“Г区间”,求实数b的最大值.
成都七中2020-2021学年度(上期)1月阶段性测试2023届高一
参考答案
一、选择题:1-5 BADAC 6-10 CBBAC 11-12 CD
二、填空题:13.[2,6] 14.0 15.-3 16.[1,e+2]
三、解答题:
17.解:(1)由x2-x-2≤0,得-1≤x≤2,则A={x|-1≤x≤2}. 因为A∩B=B,所以B?A, 又B={x|2m<x<1},且B≠?.则, 所以,m的取值范围是.
(2)∵A={x|-1≤x≤2},∴, 又B={x|2m<x<1},且B≠?. 若中只有一个整数,则-3≤2m<-2,得; 所以,m的取值范围是.
18.解:(1)∵,且;∴,即a+b=2; 又只有一个实数解;∴有且仅有一个实数解为0;∴b=1,a=1;∴
.
(2)∴;∴x+1>0;∴(x+1)f(x)>m(m-x)-1恒成立?(1+m)x>m2-1; 当m+1>0时,即m>-1时,有m-1<x恒成立?m<x+1?m<(x+1)min,∴; 当m+1<0,即m<-1时,同理可得;∴此时m不存在. 综上,m的取值范围是.
19.(1)由图象可知:,所以T=π,则, 又,k∈Z得,又,所以, 所以, 由
,k∈Z得,,k∈Z, 所以f(x)的单调递增区间为;
(2)由图象变换得g(x)=sin x,所以存在使得等式2a=-2sin2x+3sin x+1成立, 即2a=-2sin2x+3sin x+1在上有解, 令t=sin x∈[0,1],则
, 所以,即.
20.解:(1)绘制函数图象如图所示:
设f(x)的最小正周期为T,得.由得ω=1. 又解得, 令,即,k∈Z, 据此可得:,又,令k=0可得. 所以函数的解析式为.
(2)因为函数的周期为, 又k>0,所以k=3. 令,因为,所以. sin t=s在上有两个不同的解,等价于函数y=sin t与y=s的图象有两个不同的交点,∴, 所以方程f(kx)=m在时恰好有两个不同的解的条件是, 即实数m的取值范围是.
21.解:(1)因为每件商品售价为0.05万元,则x千件商品销售额为0.05×1000x万元, 依题意得:当0<x<80时,, 当x≥80时,, 所以
;
(2)当0<x<80时,, 此时,当x=30时,即L(x)≤L(30)=250万元. 当x≥80时,, 此时,x=100,即L(x)≤L(100)=200万元, 由于250>200, 所以当年产量为30千件时,该厂在这一商品生产中所获利润最大,最大利润为250万元
22.(1)h(x)在上单调递减,在[1,2]上单调递增;
(2)由题意知,, ①若,则h(x)在上单调递减,所以h(x)的最大值为 ②若1<a≤2,则h(x)在上单调递减,在[1,a]上单调递增,此时, 所以h(x)的最大值为; ③若a>2,则h(x)在上单调递减,在[1,a]上单调递增,此时, 所以h(x)的最大值为
综上知:若,则h(x)的最大值为;若a>2,则h(x)的最大值为.
(3)由(1)(2)知: ①当时,f(x)在上的值域为,f(x)在[b,2]上的值域为,∵,有,满足,?x2∈[b,2],使得f(x1)=f(x2),∴此时是f(x)的“Г区间”, ②当1<b≤2时,f(x)在上的值域为,f(x)在[b,2]上的值域为,∵当x1∈[1,b)时,,∴?x1∈[1,b),使得,即?x1∈[1,b),?x2∈[b,2],f(x1)≠f(x2)∴此时不是f(x)的“Г区间”, 综上,实数b的最大值为1.
同课章节目录
