人教版八年级数学下册课件-18.2.2 菱形2(21张)
文档属性
| 名称 | 人教版八年级数学下册课件-18.2.2 菱形2(21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 729.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 15:26:30 | ||
图片预览


文档简介
第十八章 平行四边形
菱形的性质与判定复习课
一组邻边相等
______________的平行四边形叫做菱形.
平行四边形
菱形的定义:
菱形
一组邻边相等
一、菱形的性质复习与回顾:
边
对角线
角
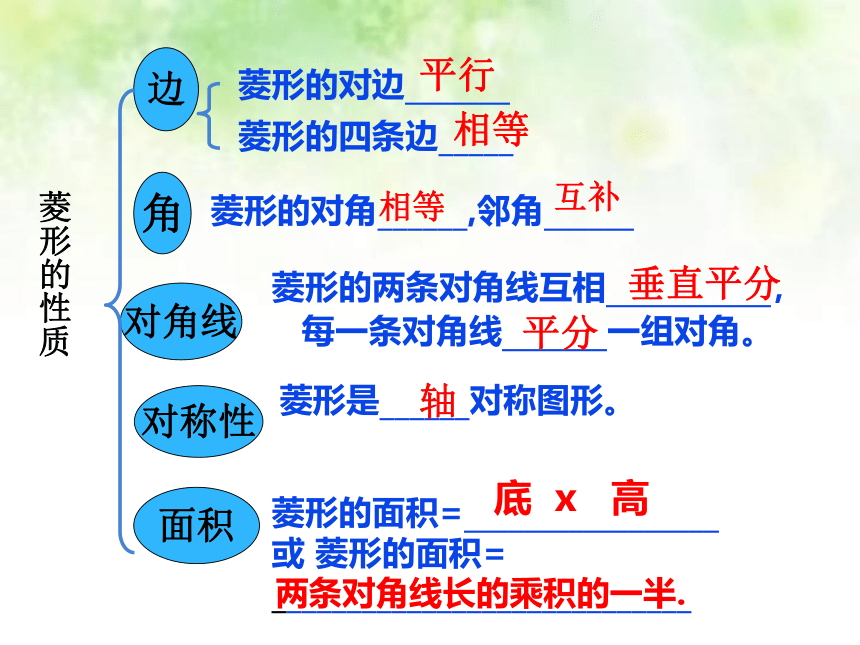
菱形的性质
菱形的对边_______
菱形的四条边_____
菱形的对角______,邻角______
菱形的两条对角线互相___________,
每一条对角线_______一组对角。
相等
平分
垂直平分
对称性
菱形是______对称图形。
轴
平行
互补
相等
菱形的面积=_________________ 或 菱形的面积= ____________________________
面积
底 x 高
两条对角线长的乘积的一半.
菱形的四条边都相等。
菱形的两条对角线互相垂直。
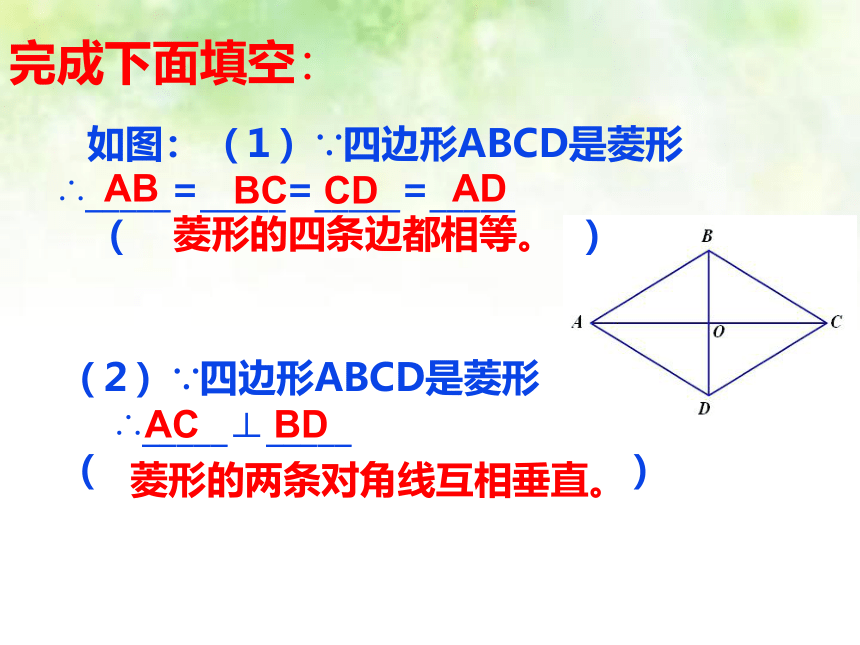
如图:(1)∵四边形ABCD是菱形 ∴_____=_____=_____=_____
( )
(2)∵四边形ABCD是菱形
∴_____⊥_____
( )
AB
BC
CD
AD
AC
BD
完成下面填空:
(3)∵四边形ABCD是菱形
∴
_____________
( )
菱形的对角线平分每一组对角
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
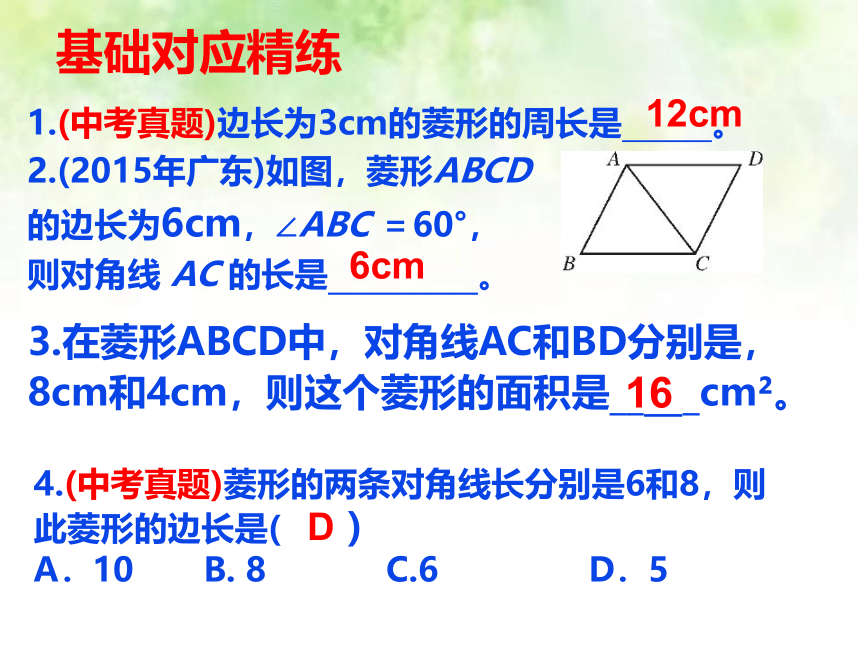
1.(中考真题)边长为3cm的菱形的周长是 。
2.(2015年广东)如图,菱形ABCD
的边长为6cm,∠ABC =60°,
则对角线 AC 的长是__________。
基础对应精练
4.(中考真题)菱形的两条对角线长分别是6和8,则
此菱形的边长是( )
A.10 B. 8 C.6 D.5
12cm
6cm
D
3.在菱形ABCD中,对角线AC和BD分别是,8cm和4cm,则这个菱形的面积是_____cm?。
16
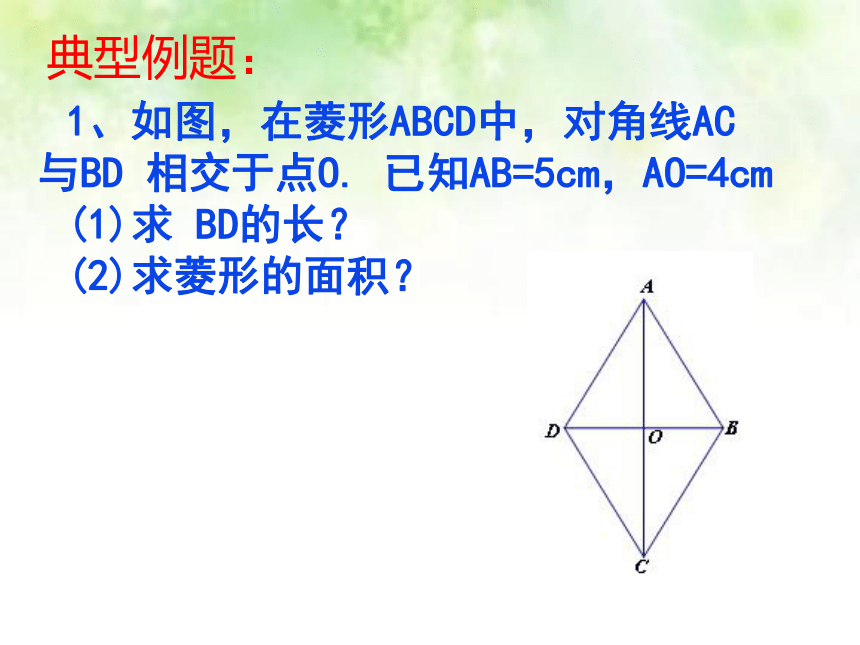
典型例题:
1、如图,在菱形ABCD中,对角线AC与BD 相交于点O. 已知AB=5cm,AO=4cm
(1)求 BD的长?
(2)求菱形的面积?
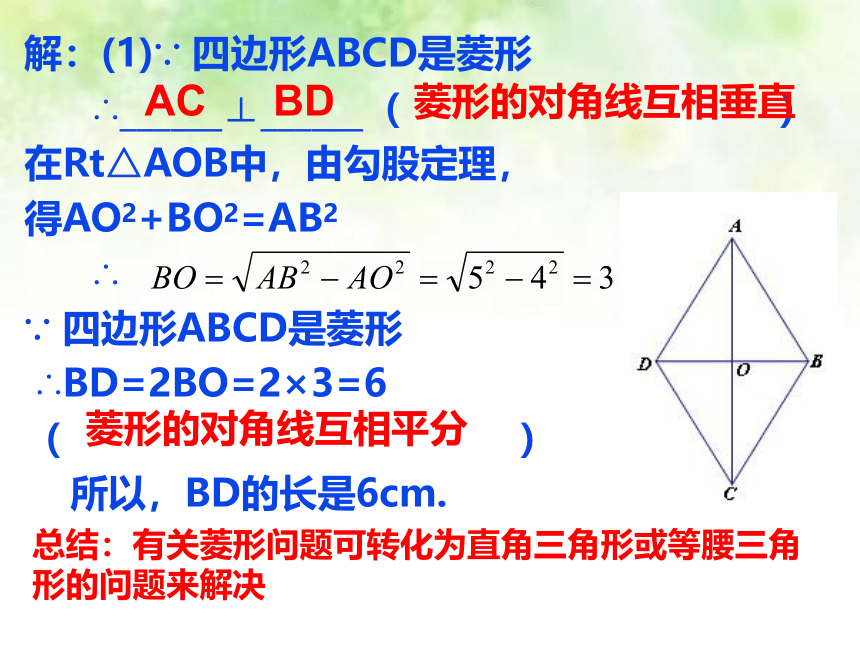
解:(1)∵ 四边形ABCD是菱形
∴______⊥______( )
在Rt△AOB中,由勾股定理,
得AO2+BO2=AB2
∴
∵ 四边形ABCD是菱形
∴BD=2BO=2×3=6
( )
所以,BD的长是6cm.
AC
BD
菱形的对角线互相平分
菱形的对角线互相垂直
总结:有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
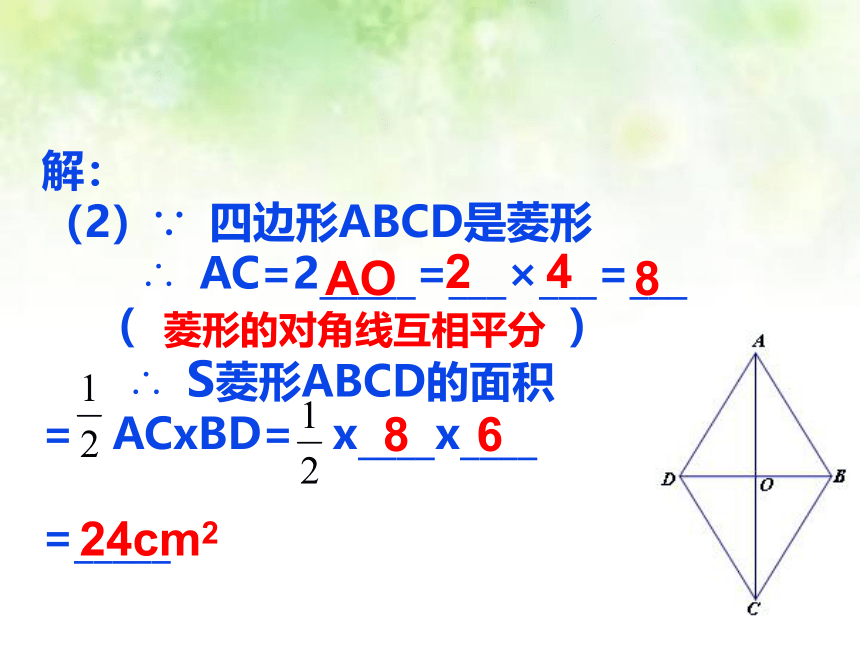
解:
(2)∵ 四边形ABCD是菱形
∴ AC=2_____=___×___=___
( )
∴ S菱形ABCD的面积 = ACxBD= x____x____
=_____
菱形的对角线互相平分
AO
2
4
8
8
6
24cm2
变式训练:如图,四边形ABCD是菱形,对角线AC与BD相交于O, AB=5,BO=4,求AC的长.?
解:∵ 四边形ABCD是菱形
∴AC⊥BD(菱形的对角线互相垂直)
在Rt△AOB中,由勾股定理,
得AO2+BO2=AB2
∴
∵ 四边形ABCD是菱形
∴AC=2AO=2×3=6
( 菱形的对角线互相平分)
所以,AC的长是6cm.
菱形的判定
边
对角线
有一组邻边_____的平行四边形是菱形.
四边______的四边形是菱形.
对角线___________的
平行四边形是菱形.
对角线___________的四边形是菱形.
二、菱形的判定复习与回顾:
相等
互相垂直
相等
互相垂直平分
如图:?∵四边形ABCD是平行四边形
又∵____________
∴四边形ABCD是菱形
( )
AB=AD
有一组邻边相等的平行四边形是菱形
完成下面填空:
判定定理1:
有一组邻边相等的平行四边形是菱形
?在四边形ABCD中,
∵_____________
∴四边形ABCD是菱形
( )
四边相等的四边形是菱形
AB=BC=CD=DA
判定定理2:
四边相等的四边形是菱形
又∵____________
∴四边形ABCD是菱形
( )
AC⊥BD
如图:
?∵四边形ABCD是平行四边形
对角线互相垂直的平行四边形是菱形
判定定理3:
对角线互相垂直的平行四边形是菱形
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试判断四边形AEDF的形状,并说明理由。
A
B
C
D
E
F
典型例题:
解:四边形AEDF是_______
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是_____________
∵ DE ∥AC
∴∠____= ∠____( )
∵ AD是△ABC的角平分线
∴ ∠_____= ∠_____
∴ ∠_____= ∠_____
∴AE=DE( )
∴ □ AEDF是菱形
( )
A
B
C
D
E
F
1
2
3
菱形
平行四边形
2
3
1
2
1
3
有一组邻边相等的平行四边形是菱形
两直线平行,内错角相等
等角对等边
A
B
C
D
O
E
变式训练:
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
证明: ∵DE∥AC,CE ∥BD.
∴ 四边形AEDF是平行四边形
又 ∵ 四边形ABCD是矩形
∴ AC=BD
OC= AC,OD= BD
∴ OC=OD
∴ □ AEDF是菱形
( 有一组邻边相等的平行四边形是菱形)
A
B
C
D
O
E
1、如图,在菱形ABCD中,AB=5,∠BAD=60°, 则对角线BD等于( )
A、20 B、15
C、10 D、5 ?
基础对应精练
2.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相垂直 D.对角线相等
D
D
3.在菱形ABCD中,AB=10cm,则菱形的周长为___________
4、菱形两条对角线的长分别是 12 和 16,则它的长为_______,面积_______。
5.菱形的面积为24,一对角线长为6,则另一对角线长为_______,边长为________
6.如图所示:在□ABCD中添加一个条件
;使其成为菱形.
AB=AD
或AC⊥BD
40cm
10
96
8
5
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
4、 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
菱形的性质与判定复习课
一组邻边相等
______________的平行四边形叫做菱形.
平行四边形
菱形的定义:
菱形
一组邻边相等
一、菱形的性质复习与回顾:
边
对角线
角
菱形的性质
菱形的对边_______
菱形的四条边_____
菱形的对角______,邻角______
菱形的两条对角线互相___________,
每一条对角线_______一组对角。
相等
平分
垂直平分
对称性
菱形是______对称图形。
轴
平行
互补
相等
菱形的面积=_________________ 或 菱形的面积= ____________________________
面积
底 x 高
两条对角线长的乘积的一半.
菱形的四条边都相等。
菱形的两条对角线互相垂直。
如图:(1)∵四边形ABCD是菱形 ∴_____=_____=_____=_____
( )
(2)∵四边形ABCD是菱形
∴_____⊥_____
( )
AB
BC
CD
AD
AC
BD
完成下面填空:
(3)∵四边形ABCD是菱形
∴
_____________
( )
菱形的对角线平分每一组对角
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
1.(中考真题)边长为3cm的菱形的周长是 。
2.(2015年广东)如图,菱形ABCD
的边长为6cm,∠ABC =60°,
则对角线 AC 的长是__________。
基础对应精练
4.(中考真题)菱形的两条对角线长分别是6和8,则
此菱形的边长是( )
A.10 B. 8 C.6 D.5
12cm
6cm
D
3.在菱形ABCD中,对角线AC和BD分别是,8cm和4cm,则这个菱形的面积是_____cm?。
16
典型例题:
1、如图,在菱形ABCD中,对角线AC与BD 相交于点O. 已知AB=5cm,AO=4cm
(1)求 BD的长?
(2)求菱形的面积?
解:(1)∵ 四边形ABCD是菱形
∴______⊥______( )
在Rt△AOB中,由勾股定理,
得AO2+BO2=AB2
∴
∵ 四边形ABCD是菱形
∴BD=2BO=2×3=6
( )
所以,BD的长是6cm.
AC
BD
菱形的对角线互相平分
菱形的对角线互相垂直
总结:有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
解:
(2)∵ 四边形ABCD是菱形
∴ AC=2_____=___×___=___
( )
∴ S菱形ABCD的面积 = ACxBD= x____x____
=_____
菱形的对角线互相平分
AO
2
4
8
8
6
24cm2
变式训练:如图,四边形ABCD是菱形,对角线AC与BD相交于O, AB=5,BO=4,求AC的长.?
解:∵ 四边形ABCD是菱形
∴AC⊥BD(菱形的对角线互相垂直)
在Rt△AOB中,由勾股定理,
得AO2+BO2=AB2
∴
∵ 四边形ABCD是菱形
∴AC=2AO=2×3=6
( 菱形的对角线互相平分)
所以,AC的长是6cm.
菱形的判定
边
对角线
有一组邻边_____的平行四边形是菱形.
四边______的四边形是菱形.
对角线___________的
平行四边形是菱形.
对角线___________的四边形是菱形.
二、菱形的判定复习与回顾:
相等
互相垂直
相等
互相垂直平分
如图:?∵四边形ABCD是平行四边形
又∵____________
∴四边形ABCD是菱形
( )
AB=AD
有一组邻边相等的平行四边形是菱形
完成下面填空:
判定定理1:
有一组邻边相等的平行四边形是菱形
?在四边形ABCD中,
∵_____________
∴四边形ABCD是菱形
( )
四边相等的四边形是菱形
AB=BC=CD=DA
判定定理2:
四边相等的四边形是菱形
又∵____________
∴四边形ABCD是菱形
( )
AC⊥BD
如图:
?∵四边形ABCD是平行四边形
对角线互相垂直的平行四边形是菱形
判定定理3:
对角线互相垂直的平行四边形是菱形
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试判断四边形AEDF的形状,并说明理由。
A
B
C
D
E
F
典型例题:
解:四边形AEDF是_______
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是_____________
∵ DE ∥AC
∴∠____= ∠____( )
∵ AD是△ABC的角平分线
∴ ∠_____= ∠_____
∴ ∠_____= ∠_____
∴AE=DE( )
∴ □ AEDF是菱形
( )
A
B
C
D
E
F
1
2
3
菱形
平行四边形
2
3
1
2
1
3
有一组邻边相等的平行四边形是菱形
两直线平行,内错角相等
等角对等边
A
B
C
D
O
E
变式训练:
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
证明: ∵DE∥AC,CE ∥BD.
∴ 四边形AEDF是平行四边形
又 ∵ 四边形ABCD是矩形
∴ AC=BD
OC= AC,OD= BD
∴ OC=OD
∴ □ AEDF是菱形
( 有一组邻边相等的平行四边形是菱形)
A
B
C
D
O
E
1、如图,在菱形ABCD中,AB=5,∠BAD=60°, 则对角线BD等于( )
A、20 B、15
C、10 D、5 ?
基础对应精练
2.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相垂直 D.对角线相等
D
D
3.在菱形ABCD中,AB=10cm,则菱形的周长为___________
4、菱形两条对角线的长分别是 12 和 16,则它的长为_______,面积_______。
5.菱形的面积为24,一对角线长为6,则另一对角线长为_______,边长为________
6.如图所示:在□ABCD中添加一个条件
;使其成为菱形.
AB=AD
或AC⊥BD
40cm
10
96
8
5
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
4、 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
