2020-2021学年九年级数学人教版下册 第二十七章 相似 训练题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册 第二十七章 相似 训练题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 902.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 17:00:20 | ||
图片预览



文档简介
人教版九年级数学下册
第二十七章
相似
训练题
一、选择题
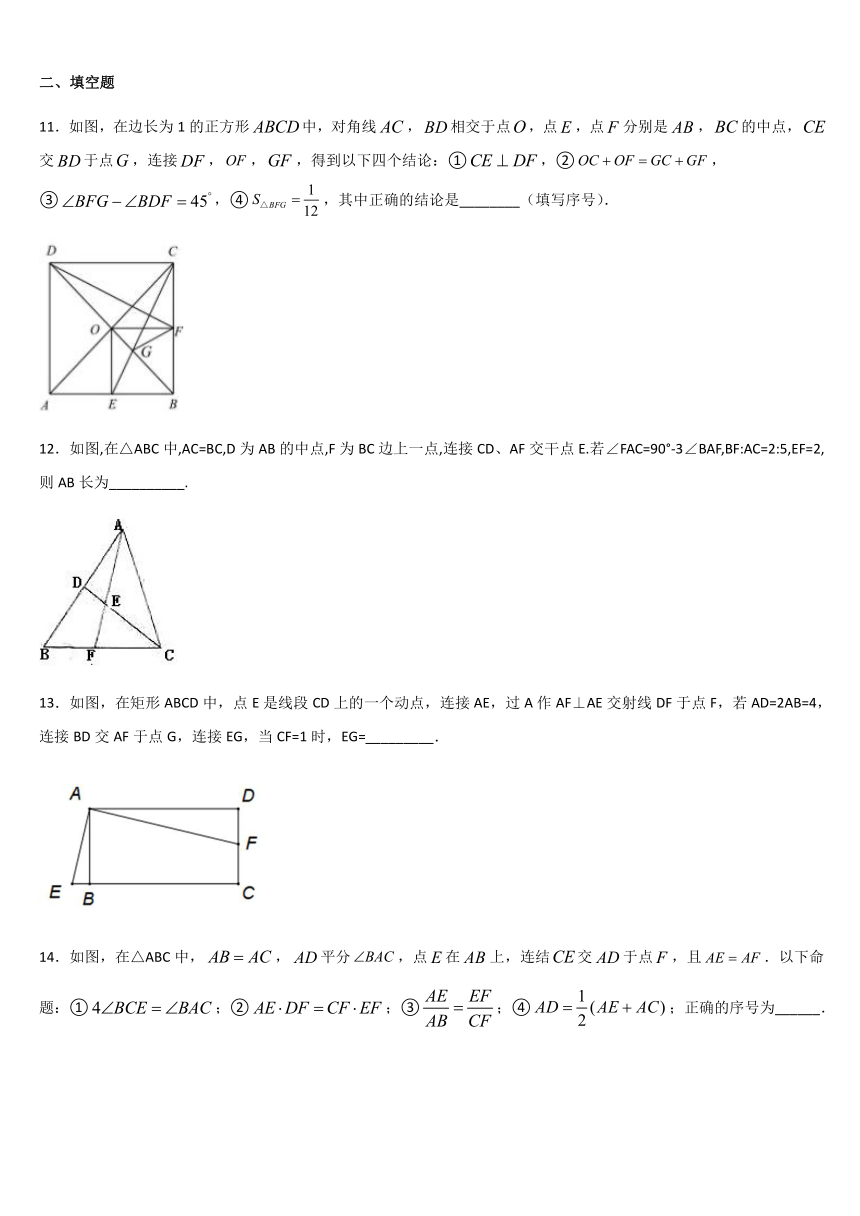
1.如图,△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC.则BN:NQ:QM等于(
)
A.6:3:2
B.2:1:1
C.5:3:2
D.1:1:1
2.如图,在中,过点作于点,过点作于点,、交于点,连接.将沿翻折得到,点恰好落在线段上且交于点.若,,,则(
)
A.
B.
C.
D.3
3.如图,在△ABC中,点O是∠ABC和∠ACB两个内角平分线的交点,过点O作EF∥BC分别交AB,AC于点E,F,已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
A.
B.
C.
D.
4.如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E、F,若CE=1,则BF的长为(
)
A.
B.
C.
D.
5.如图,矩形ABCD中,AB=2,BC=4,点P是BC边上的一个动点(点P不与点B,C重合),现将△ABP沿直线AP折叠,使点B落到点B′处;作∠B′PC的角平分线交CD于点E.设BP=x,CE=y,则下列图象中,能表示y与x的函数关系的图象大致是(
)
A.
B.
C.
D.
6.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线的图象经过点A,若S△BEC=3,则k等于(
)
A.12
B.6
C.3
D.2
7.如图,中,,,,点在内,且平分,平分,过点作直线,分别交、于点、,若与相似,则线段的长为(
)
A.5
B.
C.5或
D.6
8.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为米的竹竿的影长为米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为米,一级台阶高为米,如图所示,若此时落在地面上的影长为米,则树高为(
)
A.11.5米
B.11.75米
C.11.8米
D.12.25米
9.如图,△ABC是面积为18cm2的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为(
)
A.4
cm2
B.6
cm2
C.8cm2
D.10cm2
10.已知实数a、b、c、d满足2
005a3=2
006b3=2
007c3=2
008d3,
=
则a-1+b-1+c-1+d-1的值为(
).
A.1
B.0
C.-1
D.±1
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
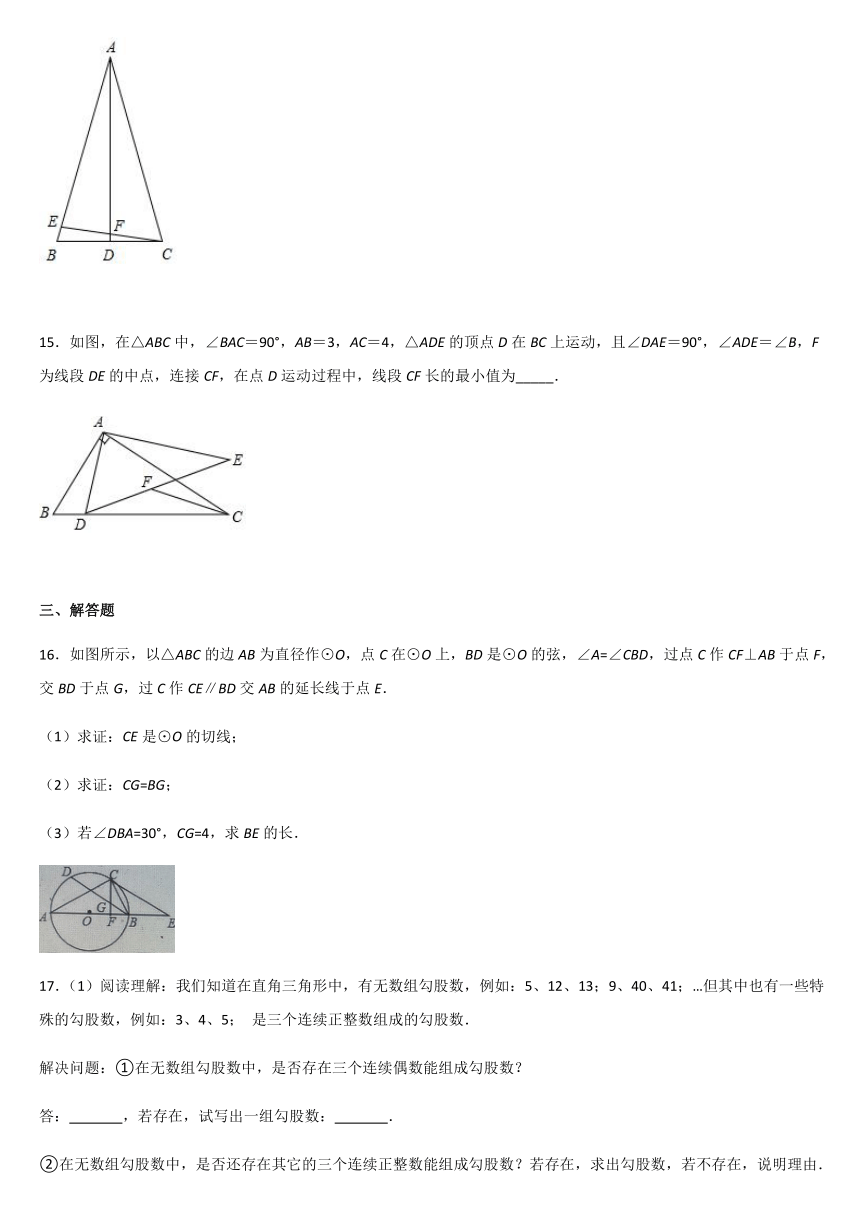
11.如图,在边长为1的正方形中,对角线,相交于点,点,点分别是,的中点,交于点,连接,,,得到以下四个结论:①,②,③,④,其中正确的结论是________(填写序号).
12.如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交干点E.若∠FAC=90°-3∠BAF,BF:AC=2:5,EF=2,则AB长为__________.
13.如图,在矩形ABCD中,点E是线段CD上的一个动点,连接AE,过A作AF⊥AE交射线DF于点F,若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,EG=_________.
14.如图,在△ABC中,,平分,点在上,连结交于点,且.以下命题:①;②;③;④;正确的序号为______.
15.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,△ADE的顶点D在BC上运动,且∠DAE=90°,∠ADE=∠B,F为线段DE的中点,连接CF,在点D运动过程中,线段CF长的最小值为_____.
三、解答题
16.如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.
17.(1)阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;…但其中也有一些特殊的勾股数,例如:3、4、5;
是三个连续正整数组成的勾股数.
解决问题:①在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答:
,若存在,试写出一组勾股数:
.
②在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
(2)探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
18.已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,点P为边AB上一动点,以P为圆心,BP为半径的圆交边BC于点Q.
(1)求AB的长;
(2)当BQ的长为时,请通过计算说明圆P与直线DC的位置关系.
19.如图,△ABC是⊙O的内接三角形,点D在上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=AB?AC;
(3)已知⊙O的半径为3.
①若=,求BC的长;
②当为何值时,AB?AC的值最大?
20.如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
21.如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC.连接
DF、EG.
(1)求证:AB=AC.
(2)已知
AB=5,BC=6.求四边形DFGE是矩形时⊙O的半径.
22.如图,直线,为垂足.以圆心,的半径作圆,交于点,,交于点,.在上任取一点,作,使,,顶点,,按顺时针方向分布,点落在射线上,且不在内.若的某一边所在直线与相切,我们称该边为的“相伴切边”.
(1)如图1,为的“相伴切边”,平分.求的长;
(2)是否存在三边中两边都是的“相伴切边”的情形?若存在,请求出的长;若不存在,请说明理由.
23.综合与实践:直角三角形折叠中的数学。数学活动:在综合实践活动课上,老师让同学们以“直角三角形纸片的折叠”为主题展开数学活动,探究折痕长度的有关问题.在中,.
(1)如图1,勤学组将点沿折叠,使得点与点重合,折痕交于点交于点则的长为
.
如图2,乐学组将点沿折叠,使得点的对应点落在边上,折痕交于点则的长为
.
(2)如图3,博学组将点沿折叠,使得点与点重合,折痕交于点交于点求线段的长度;
如图4,善思组在博学组的基础上,将点沿折叠,使得点的对应点落在上,则的长度为_
.
(3)如图5,奋进组将点沿折叠,使得点的对应点落在边上,求的长度;
如图6,创新组在奋进组的基础上,将点沿折叠,使得点的对应点落在上,折痕交于点再把展开,将点沿折叠,使得点的对应点落在的延长线上,折痕交于点得到如图7所示的图形,请直接写出的长.
【参考答案】
1.C
2.C
3.A
4.B
5.D
6.B
7.B
8.C
9.B
10.D
11.①③④
12.
13.或
14.①③④
15.2
16.(1)证明:连接OC,∵∠A=∠CBD,∴,∴OC⊥BD,∵CE∥BD,∴OC⊥CE,∴CE是⊙O的切线;
(2)证明:∵AB为直径,∴∠ACB=90°,∵CF⊥AB,∴∠ACB=∠CFB=90°,∵∠ABC=∠CBF,∴∠A=∠BCF,∵∠A=∠CBD,∴∠BCF=∠CBD,∴CG=BG;
(3)解:连接AD,∵AB为直径,∴∠ADB=90°,∵∠DBA=30°,∴∠BAD=60°,∵,∴∠DAC=∠BAC=∠BAD=30°,∴=tan30°=,∵CE∥BD,∴∠E=∠DBA=30°,∴AC=CE,∴
=,∵∠A=∠BCF=∠CBD=30°,∴∠BCE=30°,∴BE=BC,∴△CGB∽△CBE,∴
==,∵CG=4,∴BC=,∴BE=.
17.⑴①答:存在;6,8,10.
②答:不存在.
理由:假设在无数组勾股数中,还存在其它的三个连续正整数能组成勾股数.
设三个连续正整数分别是:n-1,n,n+1(n>1的整数),
则:(n-1)2+n2=(n+1)2,
得:n1=4,n2=0(舍去)
∴当n=4时,n-1=3,n+1=5,
∴三个连续正整数仍然为3,4,5,
∴不存在其它的三个连续正整数能组成勾股数.
③答:不存在.
理由:假设在无数组勾股数中,存在三个连续奇数能组成勾股数.
设三个连续奇数分别是:2n-1,2n+1,2n+3(n>1的整数),
∵(奇数)2+(奇数)2≠(奇数)2
∴不存在三个连续奇数能组成勾股数.
⑵答:存在.三边长分别是4,5,6.
理由:如图,在△ABC中,设AB=x,AC=x+1,BC=x-1(x>1的整数),
则:∠B>∠C>∠A;且∠ABC=2∠BAC,
延长CB到点D,使BD=BA,连接AD.
∴∠BAD=∠BDA,
又∵∠ABC=∠BAD+∠BDA=2∠BDA,且∠ABC=2∠BAC,
∴∠BAC=∠BDA.
又∵∠C=∠C,∴△CAB∽△CDA,
∴AC2=BC·DC,∴(x+1)2=(x-1)[(x-1)+x],
得:x1=5,x2=0(舍去).
当x=5时,x-1=4,x+1=6,即:BC=4,AB=5,AC=6,
答:存在锐角△ABC三边为连续正整数,BC=4,AB=5,AC=6;
且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC.
18.(1)过A作AE⊥BC于E,
则四边形AECD是矩形,
∴CE=AD=1,AE=CD=3,
∵AB=BC,
∴BE=AB-1,
在Rt△ABE中,∵AB2=AE2+BE2,
∴AB2=32+(AB-1)2,
解得:AB=5;
(2)过P作PF⊥BQ于F,
∴BF=BQ=,
∴△PBF∽△ABE,
∴,
∴,
∴PB=,
∴PA=AB-PB=,
过P作PG⊥CD于G交AE于M,
∴GM=AD=1,
∵DC⊥BC
∴PG∥BC
∴△APM∽△ABE,
∴,
∴,
∴PM=,
∴PG=PM+MG==PB,
∴圆P与直线DC相切.
19.(1)∵四边形EBDC为菱形,
∴∠D=∠BEC,
∵四边形ABDC是圆的内接四边形,
∴∠A+∠D=180°,
又∠BEC+∠AEC=180°,
∴∠A=∠AEC,
∴AC=CE;
(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,
由(1)知AC=CE=CD,
∴CF=CG=AC,
∵四边形AEFG是⊙C的内接四边形,
∴∠G+∠AEF=180°,
又∵∠AEF+∠BEF=180°,
∴∠G=∠BEF,
∵∠EBF=∠GBA,
∴△BEF∽△BGA,
∴,即BF?BG=BE?AB,
∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,
∴(BC﹣AC)(BC+AC)=AB?AC,即BC2﹣AC2=AB?AC;
(3)设AB=5k、AC=3k,
∵BC2﹣AC2=AB?AC,
∴BC=2k,
连接ED交BC于点M,
∵四边形BDCE是菱形,
∴DE垂直平分BC,
则点E、O、M、D共线,
在Rt△DMC中,DC=AC=3k,MC=BC=k,
∴DM=,
∴OM=OD﹣DM=3﹣k,
在Rt△COM中,由OM2+MC2=OC2得(3﹣k)2+(k)2=32,
解得:k=或k=0(舍),
∴BC=2k=4;
②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,
∴BC2=(2MC)2=36﹣4d2,
AC2=DC2=DM2+CM2=(3﹣d)2+9﹣d2,
由(2)得AB?AC=BC2﹣AC2
=﹣4d2+6d+18
=﹣4(d﹣)2+,
∴当d=,即OM=时,AB?AC最大,最大值为,
∴DC2=,
∴AC=DC=,
∴AB=,此时.
20.∵CD∥AB,
∴△EAB∽△ECD,
∴=,即=①,
∵FG∥AB,
∴△HFG∽△HAB,
∴=,即=②,
由①②得=,
解得BD=7.5,
∴=,解得:AB=7.
答:路灯杆AB的高度为7m.
21.(1)证明:∵AD、AE是⊙O的切线,
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2)如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设⊙O半径为r,
∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是⊙O直径,
∵⊙O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=BC=3,
在Rt△ABN中,AN=,
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴,即,
∴AD=r,
∴BD=AB﹣AD=5﹣r,
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴,即,
∴r=,
∴四边形DFGE是矩形时⊙O的半径为
22.(1)如图,连接OA,则,
为的“相伴切边”,
,即,
,平分,
,
则在中,;
(2)存在,求解过程如下:
由题意,分以下三种情况:
①当边AB、BC都是的“相伴切边”时,则,
,即,
点O、A、C共线,
又点C落在射线上,且不在内,
点A只能在点M或点N处,
如图2-1,当点A在点N处时,
设BC与相切于点D,连接OD,则,
,
,
;
如图2-2,当点A在点M处时,
设BC与相切于点D,连接OD,则,
,
,
;
②当边AC、BC都是的“相伴切边”时,则,
,
,即点O、A、B共线,
如图2-3,设BC与相切于点D,连接OD,则,
设,则,
,
在和中,,
,
,即,
解得或(舍去),
经检验,是所列方程的解,
则;
③当边AC、AB都是的“相伴切边”时,
是的“相伴切边”,
,即,
,
,即点O、A、B共线,
不可能是的“相伴切边”,
则边AC、AB不能同时是的“相伴切边”;
综上,AC的长为或或.
23.解:
根据折叠的性质得:AD=BD,ED⊥AB;
,∴DE//BC
∴DE是△ABC的中位线
∴DE=
由折叠的性质得BE⊥AC,
∴
∴
∴
将点沿折叠与点重合,
是的垂直平分线.
.
又
.
在Rt中,,
由勾股定理得出,则;
根据折叠的性质得出,
∴
∴∴
∴,∴
∴GF=
过点作于如图.
又
即
设
则
将点沿折叠,使得点的对应点落在边上,
解得
由折叠的性质可得
即
第二十七章
相似
训练题
一、选择题
1.如图,△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC.则BN:NQ:QM等于(
)
A.6:3:2
B.2:1:1
C.5:3:2
D.1:1:1
2.如图,在中,过点作于点,过点作于点,、交于点,连接.将沿翻折得到,点恰好落在线段上且交于点.若,,,则(
)
A.
B.
C.
D.3
3.如图,在△ABC中,点O是∠ABC和∠ACB两个内角平分线的交点,过点O作EF∥BC分别交AB,AC于点E,F,已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
A.
B.
C.
D.
4.如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E、F,若CE=1,则BF的长为(
)
A.
B.
C.
D.
5.如图,矩形ABCD中,AB=2,BC=4,点P是BC边上的一个动点(点P不与点B,C重合),现将△ABP沿直线AP折叠,使点B落到点B′处;作∠B′PC的角平分线交CD于点E.设BP=x,CE=y,则下列图象中,能表示y与x的函数关系的图象大致是(
)
A.
B.
C.
D.
6.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线的图象经过点A,若S△BEC=3,则k等于(
)
A.12
B.6
C.3
D.2
7.如图,中,,,,点在内,且平分,平分,过点作直线,分别交、于点、,若与相似,则线段的长为(
)
A.5
B.
C.5或
D.6
8.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为米的竹竿的影长为米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为米,一级台阶高为米,如图所示,若此时落在地面上的影长为米,则树高为(
)
A.11.5米
B.11.75米
C.11.8米
D.12.25米
9.如图,△ABC是面积为18cm2的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为(
)
A.4
cm2
B.6
cm2
C.8cm2
D.10cm2
10.已知实数a、b、c、d满足2
005a3=2
006b3=2
007c3=2
008d3,
=
则a-1+b-1+c-1+d-1的值为(
).
A.1
B.0
C.-1
D.±1
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,在边长为1的正方形中,对角线,相交于点,点,点分别是,的中点,交于点,连接,,,得到以下四个结论:①,②,③,④,其中正确的结论是________(填写序号).
12.如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交干点E.若∠FAC=90°-3∠BAF,BF:AC=2:5,EF=2,则AB长为__________.
13.如图,在矩形ABCD中,点E是线段CD上的一个动点,连接AE,过A作AF⊥AE交射线DF于点F,若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,EG=_________.
14.如图,在△ABC中,,平分,点在上,连结交于点,且.以下命题:①;②;③;④;正确的序号为______.
15.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,△ADE的顶点D在BC上运动,且∠DAE=90°,∠ADE=∠B,F为线段DE的中点,连接CF,在点D运动过程中,线段CF长的最小值为_____.
三、解答题
16.如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.
17.(1)阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;…但其中也有一些特殊的勾股数,例如:3、4、5;
是三个连续正整数组成的勾股数.
解决问题:①在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答:
,若存在,试写出一组勾股数:
.
②在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
(2)探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
18.已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,点P为边AB上一动点,以P为圆心,BP为半径的圆交边BC于点Q.
(1)求AB的长;
(2)当BQ的长为时,请通过计算说明圆P与直线DC的位置关系.
19.如图,△ABC是⊙O的内接三角形,点D在上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=AB?AC;
(3)已知⊙O的半径为3.
①若=,求BC的长;
②当为何值时,AB?AC的值最大?
20.如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
21.如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC.连接
DF、EG.
(1)求证:AB=AC.
(2)已知
AB=5,BC=6.求四边形DFGE是矩形时⊙O的半径.
22.如图,直线,为垂足.以圆心,的半径作圆,交于点,,交于点,.在上任取一点,作,使,,顶点,,按顺时针方向分布,点落在射线上,且不在内.若的某一边所在直线与相切,我们称该边为的“相伴切边”.
(1)如图1,为的“相伴切边”,平分.求的长;
(2)是否存在三边中两边都是的“相伴切边”的情形?若存在,请求出的长;若不存在,请说明理由.
23.综合与实践:直角三角形折叠中的数学。数学活动:在综合实践活动课上,老师让同学们以“直角三角形纸片的折叠”为主题展开数学活动,探究折痕长度的有关问题.在中,.
(1)如图1,勤学组将点沿折叠,使得点与点重合,折痕交于点交于点则的长为
.
如图2,乐学组将点沿折叠,使得点的对应点落在边上,折痕交于点则的长为
.
(2)如图3,博学组将点沿折叠,使得点与点重合,折痕交于点交于点求线段的长度;
如图4,善思组在博学组的基础上,将点沿折叠,使得点的对应点落在上,则的长度为_
.
(3)如图5,奋进组将点沿折叠,使得点的对应点落在边上,求的长度;
如图6,创新组在奋进组的基础上,将点沿折叠,使得点的对应点落在上,折痕交于点再把展开,将点沿折叠,使得点的对应点落在的延长线上,折痕交于点得到如图7所示的图形,请直接写出的长.
【参考答案】
1.C
2.C
3.A
4.B
5.D
6.B
7.B
8.C
9.B
10.D
11.①③④
12.
13.或
14.①③④
15.2
16.(1)证明:连接OC,∵∠A=∠CBD,∴,∴OC⊥BD,∵CE∥BD,∴OC⊥CE,∴CE是⊙O的切线;
(2)证明:∵AB为直径,∴∠ACB=90°,∵CF⊥AB,∴∠ACB=∠CFB=90°,∵∠ABC=∠CBF,∴∠A=∠BCF,∵∠A=∠CBD,∴∠BCF=∠CBD,∴CG=BG;
(3)解:连接AD,∵AB为直径,∴∠ADB=90°,∵∠DBA=30°,∴∠BAD=60°,∵,∴∠DAC=∠BAC=∠BAD=30°,∴=tan30°=,∵CE∥BD,∴∠E=∠DBA=30°,∴AC=CE,∴
=,∵∠A=∠BCF=∠CBD=30°,∴∠BCE=30°,∴BE=BC,∴△CGB∽△CBE,∴
==,∵CG=4,∴BC=,∴BE=.
17.⑴①答:存在;6,8,10.
②答:不存在.
理由:假设在无数组勾股数中,还存在其它的三个连续正整数能组成勾股数.
设三个连续正整数分别是:n-1,n,n+1(n>1的整数),
则:(n-1)2+n2=(n+1)2,
得:n1=4,n2=0(舍去)
∴当n=4时,n-1=3,n+1=5,
∴三个连续正整数仍然为3,4,5,
∴不存在其它的三个连续正整数能组成勾股数.
③答:不存在.
理由:假设在无数组勾股数中,存在三个连续奇数能组成勾股数.
设三个连续奇数分别是:2n-1,2n+1,2n+3(n>1的整数),
∵(奇数)2+(奇数)2≠(奇数)2
∴不存在三个连续奇数能组成勾股数.
⑵答:存在.三边长分别是4,5,6.
理由:如图,在△ABC中,设AB=x,AC=x+1,BC=x-1(x>1的整数),
则:∠B>∠C>∠A;且∠ABC=2∠BAC,
延长CB到点D,使BD=BA,连接AD.
∴∠BAD=∠BDA,
又∵∠ABC=∠BAD+∠BDA=2∠BDA,且∠ABC=2∠BAC,
∴∠BAC=∠BDA.
又∵∠C=∠C,∴△CAB∽△CDA,
∴AC2=BC·DC,∴(x+1)2=(x-1)[(x-1)+x],
得:x1=5,x2=0(舍去).
当x=5时,x-1=4,x+1=6,即:BC=4,AB=5,AC=6,
答:存在锐角△ABC三边为连续正整数,BC=4,AB=5,AC=6;
且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC.
18.(1)过A作AE⊥BC于E,
则四边形AECD是矩形,
∴CE=AD=1,AE=CD=3,
∵AB=BC,
∴BE=AB-1,
在Rt△ABE中,∵AB2=AE2+BE2,
∴AB2=32+(AB-1)2,
解得:AB=5;
(2)过P作PF⊥BQ于F,
∴BF=BQ=,
∴△PBF∽△ABE,
∴,
∴,
∴PB=,
∴PA=AB-PB=,
过P作PG⊥CD于G交AE于M,
∴GM=AD=1,
∵DC⊥BC
∴PG∥BC
∴△APM∽△ABE,
∴,
∴,
∴PM=,
∴PG=PM+MG==PB,
∴圆P与直线DC相切.
19.(1)∵四边形EBDC为菱形,
∴∠D=∠BEC,
∵四边形ABDC是圆的内接四边形,
∴∠A+∠D=180°,
又∠BEC+∠AEC=180°,
∴∠A=∠AEC,
∴AC=CE;
(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,
由(1)知AC=CE=CD,
∴CF=CG=AC,
∵四边形AEFG是⊙C的内接四边形,
∴∠G+∠AEF=180°,
又∵∠AEF+∠BEF=180°,
∴∠G=∠BEF,
∵∠EBF=∠GBA,
∴△BEF∽△BGA,
∴,即BF?BG=BE?AB,
∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,
∴(BC﹣AC)(BC+AC)=AB?AC,即BC2﹣AC2=AB?AC;
(3)设AB=5k、AC=3k,
∵BC2﹣AC2=AB?AC,
∴BC=2k,
连接ED交BC于点M,
∵四边形BDCE是菱形,
∴DE垂直平分BC,
则点E、O、M、D共线,
在Rt△DMC中,DC=AC=3k,MC=BC=k,
∴DM=,
∴OM=OD﹣DM=3﹣k,
在Rt△COM中,由OM2+MC2=OC2得(3﹣k)2+(k)2=32,
解得:k=或k=0(舍),
∴BC=2k=4;
②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,
∴BC2=(2MC)2=36﹣4d2,
AC2=DC2=DM2+CM2=(3﹣d)2+9﹣d2,
由(2)得AB?AC=BC2﹣AC2
=﹣4d2+6d+18
=﹣4(d﹣)2+,
∴当d=,即OM=时,AB?AC最大,最大值为,
∴DC2=,
∴AC=DC=,
∴AB=,此时.
20.∵CD∥AB,
∴△EAB∽△ECD,
∴=,即=①,
∵FG∥AB,
∴△HFG∽△HAB,
∴=,即=②,
由①②得=,
解得BD=7.5,
∴=,解得:AB=7.
答:路灯杆AB的高度为7m.
21.(1)证明:∵AD、AE是⊙O的切线,
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2)如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设⊙O半径为r,
∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是⊙O直径,
∵⊙O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=BC=3,
在Rt△ABN中,AN=,
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴,即,
∴AD=r,
∴BD=AB﹣AD=5﹣r,
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴,即,
∴r=,
∴四边形DFGE是矩形时⊙O的半径为
22.(1)如图,连接OA,则,
为的“相伴切边”,
,即,
,平分,
,
则在中,;
(2)存在,求解过程如下:
由题意,分以下三种情况:
①当边AB、BC都是的“相伴切边”时,则,
,即,
点O、A、C共线,
又点C落在射线上,且不在内,
点A只能在点M或点N处,
如图2-1,当点A在点N处时,
设BC与相切于点D,连接OD,则,
,
,
;
如图2-2,当点A在点M处时,
设BC与相切于点D,连接OD,则,
,
,
;
②当边AC、BC都是的“相伴切边”时,则,
,
,即点O、A、B共线,
如图2-3,设BC与相切于点D,连接OD,则,
设,则,
,
在和中,,
,
,即,
解得或(舍去),
经检验,是所列方程的解,
则;
③当边AC、AB都是的“相伴切边”时,
是的“相伴切边”,
,即,
,
,即点O、A、B共线,
不可能是的“相伴切边”,
则边AC、AB不能同时是的“相伴切边”;
综上,AC的长为或或.
23.解:
根据折叠的性质得:AD=BD,ED⊥AB;
,∴DE//BC
∴DE是△ABC的中位线
∴DE=
由折叠的性质得BE⊥AC,
∴
∴
∴
将点沿折叠与点重合,
是的垂直平分线.
.
又
.
在Rt中,,
由勾股定理得出,则;
根据折叠的性质得出,
∴
∴∴
∴,∴
∴GF=
过点作于如图.
又
即
设
则
将点沿折叠,使得点的对应点落在边上,
解得
由折叠的性质可得
即
