2020--2021学年人教版 七年级下册数学 课时训练 5.1 相交线(Word版 含答案)
文档属性
| 名称 | 2020--2021学年人教版 七年级下册数学 课时训练 5.1 相交线(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 17:08:13 | ||
图片预览

文档简介
人教版 七年级下册数学 课时训练 5.1 相交线
一、选择题
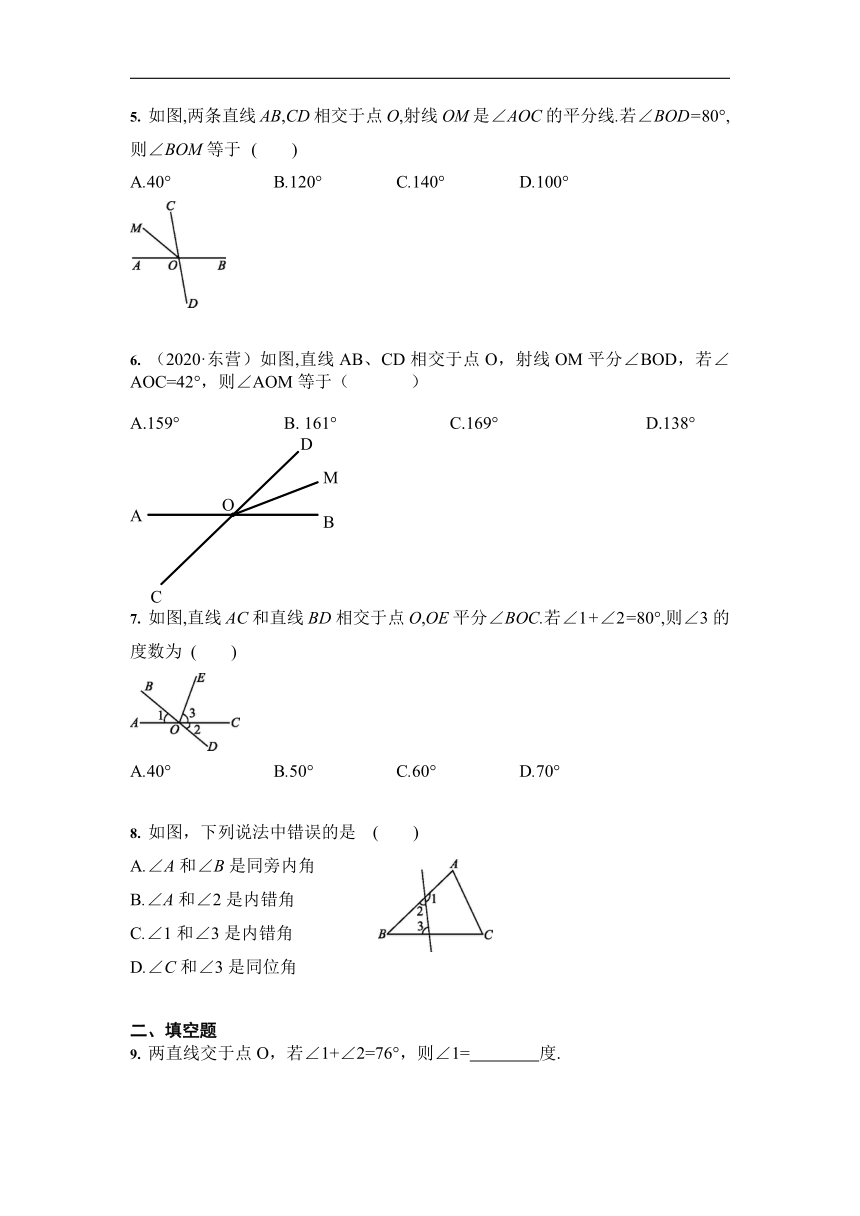
1. (2020·贵阳)(3分)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
2. (2020·安顺)如图,直线,相交于点,如果,那么是( )
A. B. C. D.
3. 如图,∠1与∠2是同位角的是 ()
A.①③ B.②③ C.③④ D.②④
4. 如图,直线AB,CD相交于点O,作射线OE,则图中邻补角有 ( )
A.4对 B.6对 C.7对 D.8对
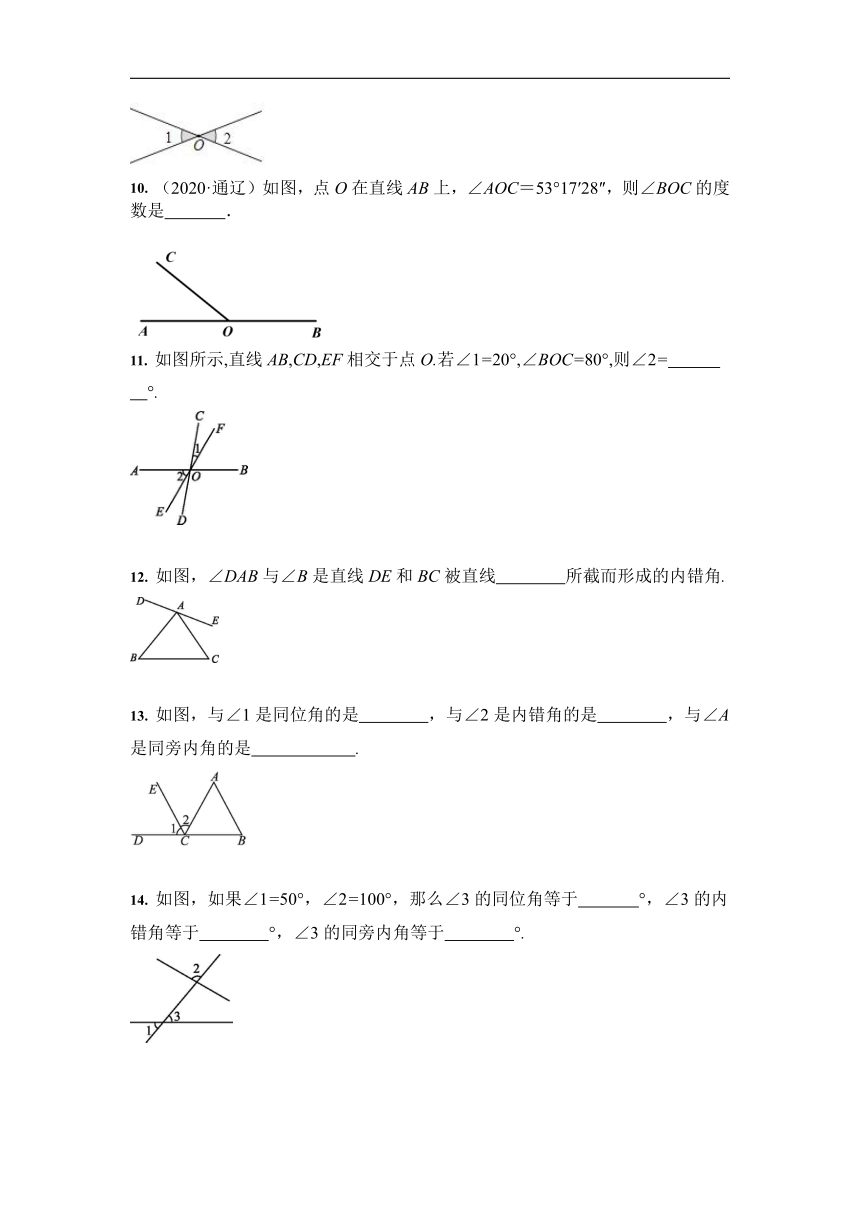
5. 如图,两条直线AB,CD相交于点O,射线OM是∠AOC的平分线.若∠BOD=80°,则∠BOM等于 ( )
A.40° B.120° C.140° D.100°
6. (2020·东营)如图,直线AB、CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于( )
A.159° B. 161° C.169° D.138°
7. 如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
8. 如图,下列说法中错误的是 ( )
A.∠A和∠B是同旁内角
B.∠A和∠2是内错角
C.∠1和∠3是内错角
D.∠C和∠3是同位角
二、填空题
9. 两直线交于点O,若∠1+∠2=76°,则∠1= 度.
10. (2020·通辽)如图,点O在直线AB上,∠AOC=53°17′28″,则∠BOC的度数是 .
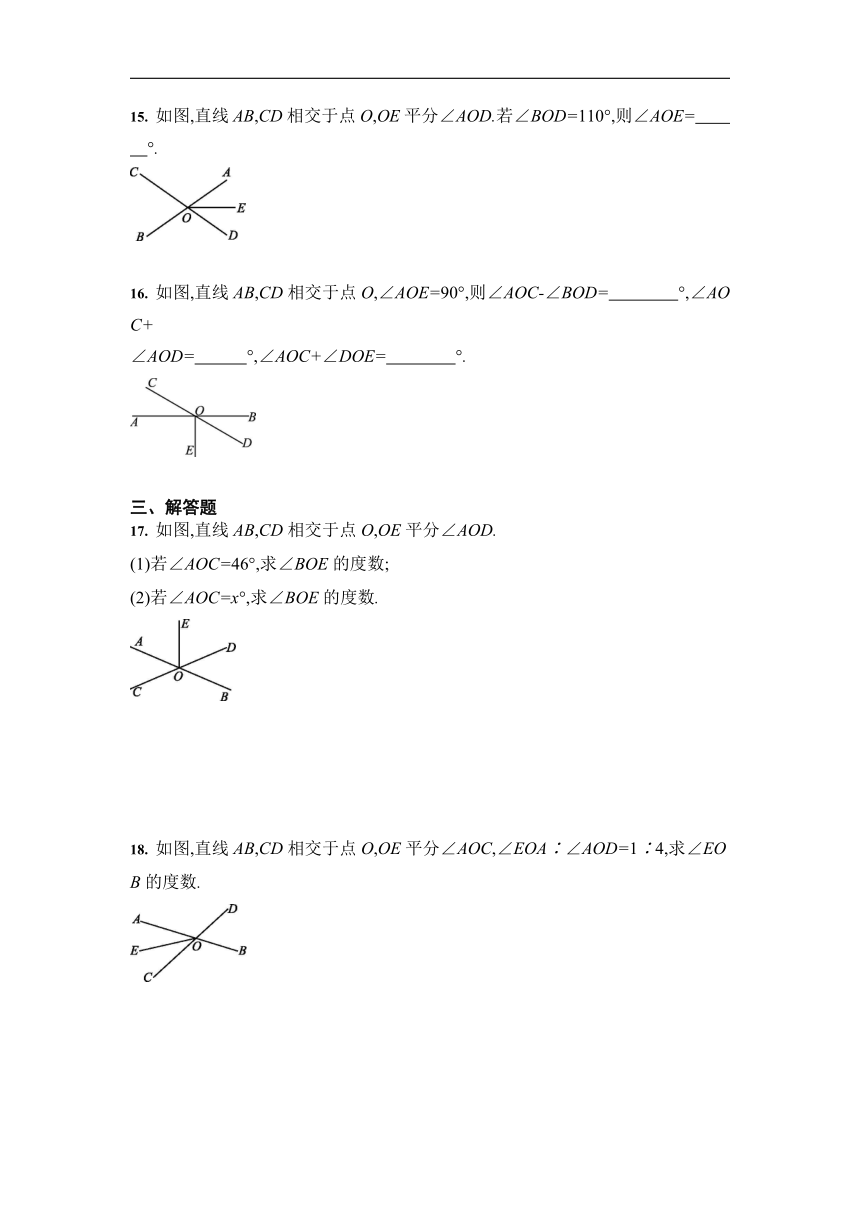
11. 如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= °.?
12. 如图,∠DAB与∠B是直线DE和BC被直线 所截而形成的内错角.?
13. 如图,与∠1是同位角的是 ,与∠2是内错角的是 ,与∠A是同旁内角的是 .?
14. 如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于 °,∠3的内错角等于 °,∠3的同旁内角等于 °.?
15. 如图,直线AB,CD相交于点O,OE平分∠AOD.若∠BOD=110°,则∠AOE= °.?
16. 如图,直线AB,CD相交于点O,∠AOE=90°,则∠AOC-∠BOD= °,∠AOC+
∠AOD= °,∠AOC+∠DOE= °.?
三、解答题
17. 如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
18. 如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
19. 如图,∠1与∠4是哪两条直线被哪一条直线所截构成的什么关系的角?∠2与∠4,∠3与∠6,∠2与∠5呢?
20. 图是一个跳棋棋盘,其游戏规则:一个棋子从某一个起始角的顶点开始,经过若干步跳动后,到达终点角的顶点.跳动时,每一步只能跳到它的同位角、内错角或同旁内角的顶点的位置上.如从起始位置∠1的顶点跳到终点位置∠3顶点的路径有
路径1:∠1∠9∠3;
路径2:∠1∠12∠6∠10∠3等.
(1)写出一条从起始位置∠1跳到终点位置∠8的路径;
(2)从起始位置∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置∠8?
(3)写出从起始位置∠1跳到终点位置∠8的路径,要求跳遍所有的角,且不能重复.
人教版 七年级下册数学 课时训练 5.1 相交线-答案
一、选择题
1. 【答案】 A
【解析】解:∵∠1+∠2=60°,∠1=∠2(对顶角相等),∴∠1=30°,
∵∠1与∠3互为邻补角,∴∠3=180°﹣∠1=180°﹣30°=150°.故选:A.
2. 【答案】A
【解析】 ∵,∴.又∵,∴.
3. 【答案】B
4. 【答案】B [解析] 邻补角有∠AOC与∠AOD,∠AOC与∠COB,∠BOD与∠AOD,∠BOD与∠COB,∠EOA与∠EOB,∠EOD与∠EOC,共6对.故选B.
5. 【答案】C [解析] 因为∠BOD=80°,所以∠AOC=80°,∠COB=100°.因为射线OM是∠AOC的平分线,所以∠COM=40°,所以∠BOM=40°+100°=140°.
6. 【答案】A
【解析】利用对顶角的性质、角的和差计算求值,借助对顶角的性质进行等角转换是关键.
由题意,可知∠AOC=42°,∴∠BOD=42°,∠AOD=138°,
∵OM平分∠BOD,∴∠DOM=21°,∴∠AOM=∠AOD +∠DOM=138°+21°=159°.
7. 【答案】D [解析] 因为∠1=∠2,∠1+∠2=80°,所以∠1=∠2=40°,所以∠BOC=140°.因为OE平分∠BOC,所以∠3=70°.故选D.
8. 【答案】B
二、填空题
9. 【答案】38°
【解析】∵两直线交于点O,∴∠1=∠2.∵∠1+∠2=76°,∠1=∠2=38°.
10. 【答案】126°42′32″
【解析】∠BOC =180°-∠AOC=180°-53°17′28″=126°42′32″.
11. 【答案】60
12. 【答案】AB
13. 【答案】∠B ∠A ∠ACB,∠B
14. 【答案】80 80 100
15. 【答案】35
16. 【答案】0 180 90
三、解答题
17. 【答案】
解:(1)因为∠AOC=46°,
所以∠AOD=180°-∠AOC=180°-46°=134°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=×134°=67°.
因为∠BOD=∠AOC=46°,
所以∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)因为∠AOC=x°,
所以∠AOD=180°-∠AOC=(180-x)°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=(180-x)°=90-x°.
因为∠BOD=∠AOC=x°,
所以∠BOE=∠DOE+∠BOD=90-x°+x°=°.
18. 【答案】
解:设∠EOA=x.因为OE平分∠AOC,
所以∠AOC=2x.
因为∠EOA∶∠AOD=1∶4,
所以∠AOD=4x.
因为∠AOC+∠AOD=180°,
所以2x+4x=180°,解得x=30°,
所以∠EOB=180°-30°=150°.
故∠EOB的度数是150°.
19. 【答案】
解:∠1与∠4是由直线AE,BD被直线AD所截构成的内错角;
∠2与∠4是由直线AB,AD被直线BD所截构成的同旁内角;
∠3与∠6是由直线BD,CD被直线BC所截构成的同位角;
∠2与∠5是由直线AB,CD被直线BD所截构成的内错角.
20. 【答案】
解:(1)答案不唯一,如∠1∠9∠8.
(2)能.路径是∠1→∠10→∠5→∠8.
(3)答案不唯一,如路径是∠1→∠9→∠2→∠10→∠3→∠4→∠11→∠5→∠6→∠12→∠7→∠8.
一、选择题
1. (2020·贵阳)(3分)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
2. (2020·安顺)如图,直线,相交于点,如果,那么是( )
A. B. C. D.
3. 如图,∠1与∠2是同位角的是 ()
A.①③ B.②③ C.③④ D.②④
4. 如图,直线AB,CD相交于点O,作射线OE,则图中邻补角有 ( )
A.4对 B.6对 C.7对 D.8对
5. 如图,两条直线AB,CD相交于点O,射线OM是∠AOC的平分线.若∠BOD=80°,则∠BOM等于 ( )
A.40° B.120° C.140° D.100°
6. (2020·东营)如图,直线AB、CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于( )
A.159° B. 161° C.169° D.138°
7. 如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
8. 如图,下列说法中错误的是 ( )
A.∠A和∠B是同旁内角
B.∠A和∠2是内错角
C.∠1和∠3是内错角
D.∠C和∠3是同位角
二、填空题
9. 两直线交于点O,若∠1+∠2=76°,则∠1= 度.
10. (2020·通辽)如图,点O在直线AB上,∠AOC=53°17′28″,则∠BOC的度数是 .
11. 如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= °.?
12. 如图,∠DAB与∠B是直线DE和BC被直线 所截而形成的内错角.?
13. 如图,与∠1是同位角的是 ,与∠2是内错角的是 ,与∠A是同旁内角的是 .?
14. 如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于 °,∠3的内错角等于 °,∠3的同旁内角等于 °.?
15. 如图,直线AB,CD相交于点O,OE平分∠AOD.若∠BOD=110°,则∠AOE= °.?
16. 如图,直线AB,CD相交于点O,∠AOE=90°,则∠AOC-∠BOD= °,∠AOC+
∠AOD= °,∠AOC+∠DOE= °.?
三、解答题
17. 如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
18. 如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
19. 如图,∠1与∠4是哪两条直线被哪一条直线所截构成的什么关系的角?∠2与∠4,∠3与∠6,∠2与∠5呢?
20. 图是一个跳棋棋盘,其游戏规则:一个棋子从某一个起始角的顶点开始,经过若干步跳动后,到达终点角的顶点.跳动时,每一步只能跳到它的同位角、内错角或同旁内角的顶点的位置上.如从起始位置∠1的顶点跳到终点位置∠3顶点的路径有
路径1:∠1∠9∠3;
路径2:∠1∠12∠6∠10∠3等.
(1)写出一条从起始位置∠1跳到终点位置∠8的路径;
(2)从起始位置∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置∠8?
(3)写出从起始位置∠1跳到终点位置∠8的路径,要求跳遍所有的角,且不能重复.
人教版 七年级下册数学 课时训练 5.1 相交线-答案
一、选择题
1. 【答案】 A
【解析】解:∵∠1+∠2=60°,∠1=∠2(对顶角相等),∴∠1=30°,
∵∠1与∠3互为邻补角,∴∠3=180°﹣∠1=180°﹣30°=150°.故选:A.
2. 【答案】A
【解析】 ∵,∴.又∵,∴.
3. 【答案】B
4. 【答案】B [解析] 邻补角有∠AOC与∠AOD,∠AOC与∠COB,∠BOD与∠AOD,∠BOD与∠COB,∠EOA与∠EOB,∠EOD与∠EOC,共6对.故选B.
5. 【答案】C [解析] 因为∠BOD=80°,所以∠AOC=80°,∠COB=100°.因为射线OM是∠AOC的平分线,所以∠COM=40°,所以∠BOM=40°+100°=140°.
6. 【答案】A
【解析】利用对顶角的性质、角的和差计算求值,借助对顶角的性质进行等角转换是关键.
由题意,可知∠AOC=42°,∴∠BOD=42°,∠AOD=138°,
∵OM平分∠BOD,∴∠DOM=21°,∴∠AOM=∠AOD +∠DOM=138°+21°=159°.
7. 【答案】D [解析] 因为∠1=∠2,∠1+∠2=80°,所以∠1=∠2=40°,所以∠BOC=140°.因为OE平分∠BOC,所以∠3=70°.故选D.
8. 【答案】B
二、填空题
9. 【答案】38°
【解析】∵两直线交于点O,∴∠1=∠2.∵∠1+∠2=76°,∠1=∠2=38°.
10. 【答案】126°42′32″
【解析】∠BOC =180°-∠AOC=180°-53°17′28″=126°42′32″.
11. 【答案】60
12. 【答案】AB
13. 【答案】∠B ∠A ∠ACB,∠B
14. 【答案】80 80 100
15. 【答案】35
16. 【答案】0 180 90
三、解答题
17. 【答案】
解:(1)因为∠AOC=46°,
所以∠AOD=180°-∠AOC=180°-46°=134°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=×134°=67°.
因为∠BOD=∠AOC=46°,
所以∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)因为∠AOC=x°,
所以∠AOD=180°-∠AOC=(180-x)°.
因为OE平分∠AOD,
所以∠DOE=∠AOD=(180-x)°=90-x°.
因为∠BOD=∠AOC=x°,
所以∠BOE=∠DOE+∠BOD=90-x°+x°=°.
18. 【答案】
解:设∠EOA=x.因为OE平分∠AOC,
所以∠AOC=2x.
因为∠EOA∶∠AOD=1∶4,
所以∠AOD=4x.
因为∠AOC+∠AOD=180°,
所以2x+4x=180°,解得x=30°,
所以∠EOB=180°-30°=150°.
故∠EOB的度数是150°.
19. 【答案】
解:∠1与∠4是由直线AE,BD被直线AD所截构成的内错角;
∠2与∠4是由直线AB,AD被直线BD所截构成的同旁内角;
∠3与∠6是由直线BD,CD被直线BC所截构成的同位角;
∠2与∠5是由直线AB,CD被直线BD所截构成的内错角.
20. 【答案】
解:(1)答案不唯一,如∠1∠9∠8.
(2)能.路径是∠1→∠10→∠5→∠8.
(3)答案不唯一,如路径是∠1→∠9→∠2→∠10→∠3→∠4→∠11→∠5→∠6→∠12→∠7→∠8.
