2020-2021学年人教版小学三年级数学下册《第八章 数学广角—搭配(二)》单元测试题(有答案)
文档属性
| 名称 | 2020-2021学年人教版小学三年级数学下册《第八章 数学广角—搭配(二)》单元测试题(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 337.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 00:00:00 | ||
图片预览




文档简介
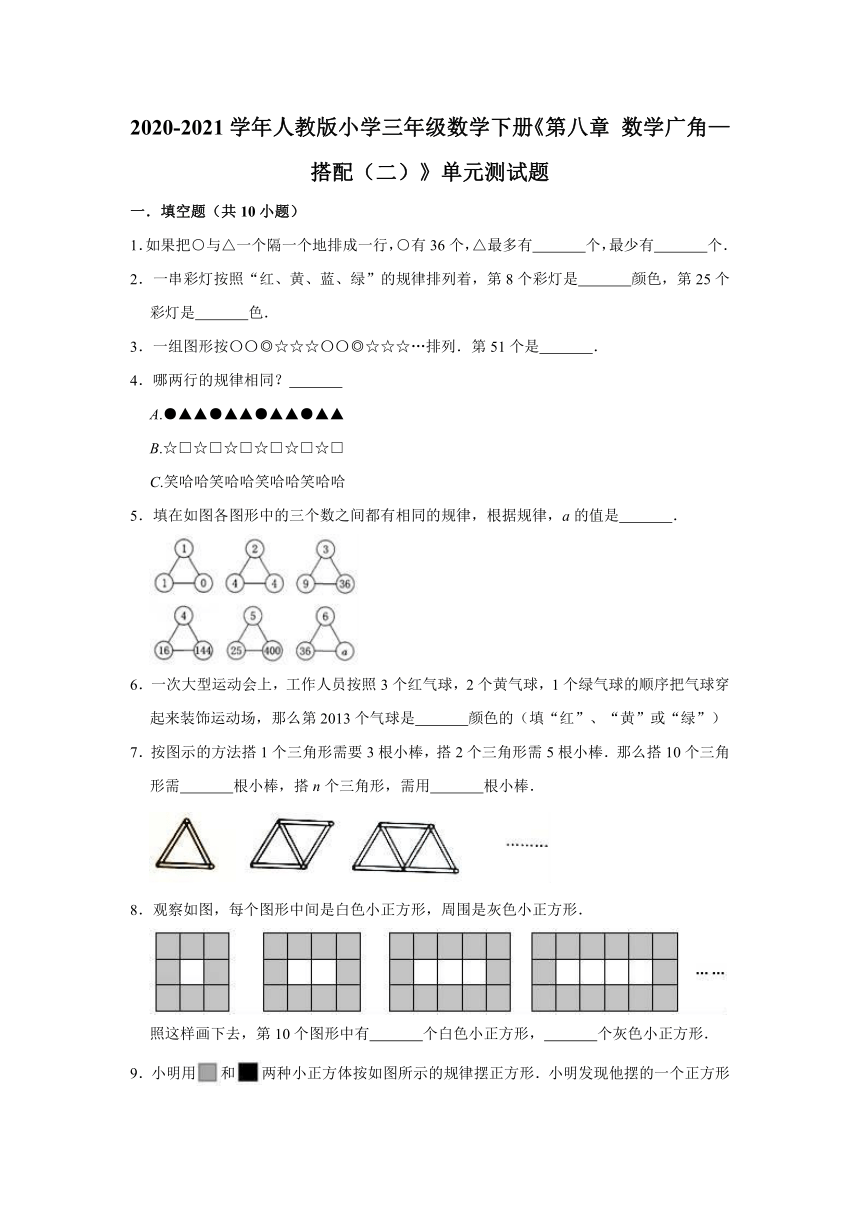
2020-2021学年人教版小学三年级数学下册《第八章
数学广角—搭配(二)》单元测试题
一.填空题(共10小题)
1.如果把○与△一个隔一个地排成一行,○有36个,△最多有
个,最少有
个.
2.一串彩灯按照“红、黄、蓝、绿”的规律排列着,第8个彩灯是
颜色,第25个彩灯是
色.
3.一组图形按〇〇◎☆☆☆〇〇◎☆☆☆…排列.第51个是
.
4.哪两行的规律相同?
A.●▲▲●▲▲●▲▲●▲▲
B.☆□☆□☆□☆□☆□☆□
C.笑哈哈笑哈哈笑哈哈笑哈哈
5.填在如图各图形中的三个数之间都有相同的规律,根据规律,a的值是
.
6.一次大型运动会上,工作人员按照3个红气球,2个黄气球,1个绿气球的顺序把气球穿起来装饰运动场,那么第2013个气球是
颜色的(填“红”、“黄”或“绿”)
7.按图示的方法搭1个三角形需要3根小棒,搭2个三角形需5根小棒.那么搭10个三角形需
根小棒,搭n个三角形,需用
根小棒.
8.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.
照这样画下去,第10个图形中有
个白色小正方形,
个灰色小正方形.
9.小明用和两种小正方体按如图所示的规律摆正方形.小明发现他摆的一个正方形中,比多9个.小明摆这个正方形,使用了
个.
10.把边长1厘米的正方形纸片,按下面的规律拼成长方形(如图).周长分别是4厘米,6厘米,8厘米,10厘米……那么,用10个正方形拼成的长方形周长是
厘米.
二.选择题(共8小题)
11.按照如图的方法用灰色和白色正方形摆图形.当中间摆a个灰色的正方形时,四周共摆( )个白色正方形.
A.2a+6
B.a+8
C.a+6
12.接着该摆( )
A.
B.
C.
13.观察下面图形的排列情况,第2012个图形是( )
△△○▽○△△○▽○…
A.△
B.○
C.▽
D.无法确定
14.□□★▲★◎◎◎□□★▲★◎◎◎□□★▲★◎◎◎□□…中排在第43个的是( )
A.□
B.★
C.▲
D.◎
15.接着如图摆( )
A.
B.
C.
16.按照“”的规律画图形,第830个图形是( )
A.
B.
C.
D.
17.观察如图中三角形个数的规律,第5个图形中共有( )个三角形.
A.12
B.15
C.18
D.21
18.有同样大小的红、黑、白纸片共79张,它们按一张红纸、两张黑纸、三张白纸的顺序排列着,第76张是( )色纸.
A.红
B.黑
C.白
三.判断题(共5小题)
19.如果把一个□和一个△一个隔一个地排成一行,有15个□,△最少有15个
.(判断对错)
20.如图,第五个点阵中点的个数是17个.
(判断对错)
21.…,第五个点阵中点的个数是1+4×5=21.
.(判断对错)
22.在下面图案排列中,第57个图案是⊙.
(判断对错)
□⊙⊙◇◇◇□⊙⊙◇◇◇□⊙⊙◇◇◇….
23.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒.
.(判断对错)
四.操作题(共3小题)
24.想一想,剩下的两张纸上应该怎么画?
25.米子格中的阴影表示8,请在图中画上斜线,表示出12。
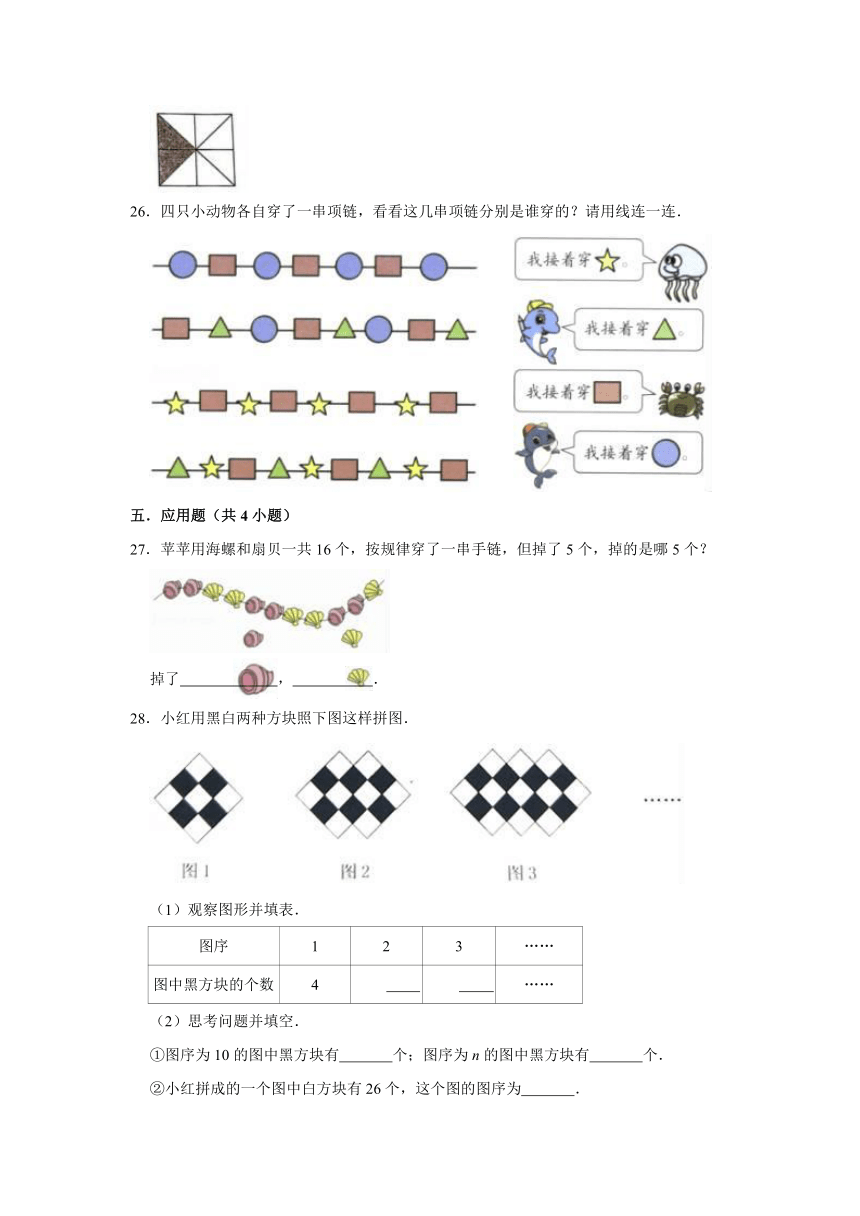
26.四只小动物各自穿了一串项链,看看这几串项链分别是谁穿的?请用线连一连.
五.应用题(共4小题)
27.苹苹用海螺和扇贝一共16个,按规律穿了一串手链,但掉了5个,掉的是哪5个?
掉了
,
.
28.小红用黑白两种方块照下图这样拼图.
(1)观察图形并填表.
图序
1
2
3
……
图中黑方块的个数
4
……
(2)思考问题并填空.
①图序为10的图中黑方块有
个;图序为n的图中黑方块有
个.
②小红拼成的一个图中白方块有26个,这个图的图序为
.
29.用“”“”和“”画出一组有规律的图形.
30.盐渎公园要铺设一条人行道,人行道长160米,宽1.6米,现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
(1)请算算铺设这条人行道一共需多少块地砖?
(2)铺设这条人行道共需要多少块红色地砖?
参考答案与试题解析
一.填空题(共10小题)
1.解:根据以上方向,得:如果把○与△一个隔一个地排成一行,○有36个,△可能有36个,可能有35个,也可能有37个;
故答案为:37,35.
2.解:8÷4=2,
所以第8盏彩灯是第二个循环周期的最后一个,是绿色;
25÷4=6…1,
所以第25个是第7循环周期的第一个,是红色的.
故答案为:绿;红.
3.解:51÷6=8…3;
所以第51个是第9周期的第3个图形是◎;
故答案为:◎.
4.解:选项A和选项C这两行的规律相同,它们都是每3个图形一循环,第一个都是一个图形或字,后两个都是相同的图形或字。
故选:A和C。
5.解:根据题干分析可得:25×36=900
答:a的值是900.
故答案为:900.
6.解:2013÷6=335…3,
所以第2013个气球是第336周期的第3个,是红气球.
故答案为:红.
7.解:摆1个三角形需小棒:3根
摆2个三角形需小棒3+2=5(根)
摆3个三角形需要小棒:3+2+2=7(根)
摆4个三角形需要小棒:3+2+2+2=9(根)
……
摆n个三角形需要小棒:3+2(n﹣1)=(2n+1)根
……
摆10个三角形需要小棒:
10×2+1
=20+1
=21(根)
答:摆10个三角形需21根小棒,摆n个三角形,需用(2n+1)根小棒.
故答案为:21;(2n+1).
8.解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)
第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)
……
第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个
所以第10个图形白色小正方形的个数为:10个
灰色小正方形的个数为:6+2×10=26(个)
答:第10个图形中有10个白色小正方形,26个灰色小正方形.
故答案为:10;26.
9.解:的个数规律为:0,3,3,10,10,21,21,36,36……;
的个数规律为:1,1,6,6,15,15,28,28,45……,
则小明摆这个正方形,使用了45个。
故答案为:45。
10.解:1个正方形的周长4厘米=4+(1﹣1)×2(厘米)
2个正方形拼成的长方形周长6厘米=4+(2﹣1)×2(厘米)
3个正方形拼成的长方形周长8厘米=4+(3﹣1)×2(厘米)
4个正方形拼成的长方形周长10厘米=4+(4﹣1)×2(厘米)
得出规律,n个正方形拼成的长方形周长为4+(n﹣1)×2(厘米)
所以10个正方形拼成的长方形周长为:
4+(10﹣1)×2
=4+9×2
=4+18
=22(厘米)
答:用10个正方形拼成的长方形的周长是22厘米.
故答案为:22.
二.选择题(共8小题)
11.解:当中间摆a个灰色的正方形时,四周共需要摆白色正方形:
2+(a+2)×2=2a+6(个)
答:当中间摆a个灰色的正方形时,四周共需要摆(2a+6)个白色正方形.
故选:A.
12.解:根据图形排列的规律,接着应该摆.
故选:C.
13.解:2012÷5=402…2,
余数是2,所以第2012个图形是一个周期里的第2个图形,即△.
故选:A.
14.解:43÷(2+1+1+1+3),
=43÷8,
=5(个)…3(个),
余数是3,所以排在第43个的是★.
故选:B.
15.解:排列规律是4个图形一组,第1个是正方体,第2个是球,第3个是圆柱,第4个是球,所以按照这个规律接着该摆正方体.
故选:B.
16.解:830÷8=103……6,
可以看出,第830个图形是第104组的第6个图形,是圆.
故选:C.
17.解:三角形的个数依次为:6、9、12……,
可知,前一个图形的三角形数量比后一个少3个,
第5个图形有三角形:
12+3+3
=15+3
=18(个)
故选:C.
18.解:76÷(1+2+3),
=76÷6,
=12…4,
所以第76张纸是第13周期的第4张,是白纸.
故选:C.
三.判断题(共5小题)
19.解:根据以上方向,得:如果把□与△一个隔一个地排成一行,□有15个,△可能有
15个,可能有
14个,也可能有
16个;
所以如果把一个□和一个△一个隔一个地排成一行,有15个□,△最少有15个的说法是错误的;
故答案为:×.
20.解:第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
故答案为:√.
21.解:根据题干分析可得:第n点阵的点数=1+(n﹣1)×4,
n=5时,点数个数为:1+(5﹣1)×4=17.
所以原题说法错误.
故答案为:×.
22.解:57÷6=9…3,
所以第57个图形是第10循环周期的第3个图形,是⊙.
故答案为:√.
23.解:摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
…,
所以摆n个正方形要小棒:4+3×(n﹣1)=3n+1(根);
n=10,3×10+1=31(根);
答:摆10个正方形一共需要31根小棒.
原题说法正确.
故答案为:√.
四.操作题(共3小题)
24.解:
25.解:12÷(8÷2)
=12÷4
=3(份)
答:3份表示12。
如图斜线部分:
。
26.解:
五.应用题(共4小题)
27.解:
掉了
2,3.
故答案为:2,3.
28.解:(1)填表如下:
图序
1
2
3
……
图中黑方块的个数
4
6
8
……
(2)①图1黑色方块4个
图2黑色方块4+2=6(个)
图3黑色方块:4+2+2=8(个)
……
图10黑方块的个数:
2×10+2
=20+2
=22(个)
……
第n个图形黑色方块的个数为:4+2(n﹣1)=(2n+2)个
答:图序为10的图中黑方块有22个;图序为n的图中黑方块有(2n+2)个.
②白方块的排列规律为:
图1:5个
图2:5+3=9(个)
图3:5+3+3=11(个)
……
第n个图形白方块个数:5+3(n﹣1)=(3n+2)个
3n+2=26
3n=24
n=8
答:白方块有26个,这个图的图序为8.
故答案为:6,8;22,(2n+2);8.
29.解:如图:
每3个图形一循环,分别是:、、.
(答案不唯一.)
30.解:(1)每块地砖的边长为:
1.6÷4=0.4(米)
需要地砖的块数:
160×1.6÷0.42
=160×1.6÷0.16
=160×10
=1600(块)
答:铺设这条人行道一共需1600块地砖。
(2)将图形按4×4分组,共有:
160÷16=100(组)
红色地砖有:
100×4=400(块)
答:铺设这条人行道共需要400块红色地砖。
数学广角—搭配(二)》单元测试题
一.填空题(共10小题)
1.如果把○与△一个隔一个地排成一行,○有36个,△最多有
个,最少有
个.
2.一串彩灯按照“红、黄、蓝、绿”的规律排列着,第8个彩灯是
颜色,第25个彩灯是
色.
3.一组图形按〇〇◎☆☆☆〇〇◎☆☆☆…排列.第51个是
.
4.哪两行的规律相同?
A.●▲▲●▲▲●▲▲●▲▲
B.☆□☆□☆□☆□☆□☆□
C.笑哈哈笑哈哈笑哈哈笑哈哈
5.填在如图各图形中的三个数之间都有相同的规律,根据规律,a的值是
.
6.一次大型运动会上,工作人员按照3个红气球,2个黄气球,1个绿气球的顺序把气球穿起来装饰运动场,那么第2013个气球是
颜色的(填“红”、“黄”或“绿”)
7.按图示的方法搭1个三角形需要3根小棒,搭2个三角形需5根小棒.那么搭10个三角形需
根小棒,搭n个三角形,需用
根小棒.
8.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.
照这样画下去,第10个图形中有
个白色小正方形,
个灰色小正方形.
9.小明用和两种小正方体按如图所示的规律摆正方形.小明发现他摆的一个正方形中,比多9个.小明摆这个正方形,使用了
个.
10.把边长1厘米的正方形纸片,按下面的规律拼成长方形(如图).周长分别是4厘米,6厘米,8厘米,10厘米……那么,用10个正方形拼成的长方形周长是
厘米.
二.选择题(共8小题)
11.按照如图的方法用灰色和白色正方形摆图形.当中间摆a个灰色的正方形时,四周共摆( )个白色正方形.
A.2a+6
B.a+8
C.a+6
12.接着该摆( )
A.
B.
C.
13.观察下面图形的排列情况,第2012个图形是( )
△△○▽○△△○▽○…
A.△
B.○
C.▽
D.无法确定
14.□□★▲★◎◎◎□□★▲★◎◎◎□□★▲★◎◎◎□□…中排在第43个的是( )
A.□
B.★
C.▲
D.◎
15.接着如图摆( )
A.
B.
C.
16.按照“”的规律画图形,第830个图形是( )
A.
B.
C.
D.
17.观察如图中三角形个数的规律,第5个图形中共有( )个三角形.
A.12
B.15
C.18
D.21
18.有同样大小的红、黑、白纸片共79张,它们按一张红纸、两张黑纸、三张白纸的顺序排列着,第76张是( )色纸.
A.红
B.黑
C.白
三.判断题(共5小题)
19.如果把一个□和一个△一个隔一个地排成一行,有15个□,△最少有15个
.(判断对错)
20.如图,第五个点阵中点的个数是17个.
(判断对错)
21.…,第五个点阵中点的个数是1+4×5=21.
.(判断对错)
22.在下面图案排列中,第57个图案是⊙.
(判断对错)
□⊙⊙◇◇◇□⊙⊙◇◇◇□⊙⊙◇◇◇….
23.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒.
.(判断对错)
四.操作题(共3小题)
24.想一想,剩下的两张纸上应该怎么画?
25.米子格中的阴影表示8,请在图中画上斜线,表示出12。
26.四只小动物各自穿了一串项链,看看这几串项链分别是谁穿的?请用线连一连.
五.应用题(共4小题)
27.苹苹用海螺和扇贝一共16个,按规律穿了一串手链,但掉了5个,掉的是哪5个?
掉了
,
.
28.小红用黑白两种方块照下图这样拼图.
(1)观察图形并填表.
图序
1
2
3
……
图中黑方块的个数
4
……
(2)思考问题并填空.
①图序为10的图中黑方块有
个;图序为n的图中黑方块有
个.
②小红拼成的一个图中白方块有26个,这个图的图序为
.
29.用“”“”和“”画出一组有规律的图形.
30.盐渎公园要铺设一条人行道,人行道长160米,宽1.6米,现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
(1)请算算铺设这条人行道一共需多少块地砖?
(2)铺设这条人行道共需要多少块红色地砖?
参考答案与试题解析
一.填空题(共10小题)
1.解:根据以上方向,得:如果把○与△一个隔一个地排成一行,○有36个,△可能有36个,可能有35个,也可能有37个;
故答案为:37,35.
2.解:8÷4=2,
所以第8盏彩灯是第二个循环周期的最后一个,是绿色;
25÷4=6…1,
所以第25个是第7循环周期的第一个,是红色的.
故答案为:绿;红.
3.解:51÷6=8…3;
所以第51个是第9周期的第3个图形是◎;
故答案为:◎.
4.解:选项A和选项C这两行的规律相同,它们都是每3个图形一循环,第一个都是一个图形或字,后两个都是相同的图形或字。
故选:A和C。
5.解:根据题干分析可得:25×36=900
答:a的值是900.
故答案为:900.
6.解:2013÷6=335…3,
所以第2013个气球是第336周期的第3个,是红气球.
故答案为:红.
7.解:摆1个三角形需小棒:3根
摆2个三角形需小棒3+2=5(根)
摆3个三角形需要小棒:3+2+2=7(根)
摆4个三角形需要小棒:3+2+2+2=9(根)
……
摆n个三角形需要小棒:3+2(n﹣1)=(2n+1)根
……
摆10个三角形需要小棒:
10×2+1
=20+1
=21(根)
答:摆10个三角形需21根小棒,摆n个三角形,需用(2n+1)根小棒.
故答案为:21;(2n+1).
8.解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)
第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)
……
第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个
所以第10个图形白色小正方形的个数为:10个
灰色小正方形的个数为:6+2×10=26(个)
答:第10个图形中有10个白色小正方形,26个灰色小正方形.
故答案为:10;26.
9.解:的个数规律为:0,3,3,10,10,21,21,36,36……;
的个数规律为:1,1,6,6,15,15,28,28,45……,
则小明摆这个正方形,使用了45个。
故答案为:45。
10.解:1个正方形的周长4厘米=4+(1﹣1)×2(厘米)
2个正方形拼成的长方形周长6厘米=4+(2﹣1)×2(厘米)
3个正方形拼成的长方形周长8厘米=4+(3﹣1)×2(厘米)
4个正方形拼成的长方形周长10厘米=4+(4﹣1)×2(厘米)
得出规律,n个正方形拼成的长方形周长为4+(n﹣1)×2(厘米)
所以10个正方形拼成的长方形周长为:
4+(10﹣1)×2
=4+9×2
=4+18
=22(厘米)
答:用10个正方形拼成的长方形的周长是22厘米.
故答案为:22.
二.选择题(共8小题)
11.解:当中间摆a个灰色的正方形时,四周共需要摆白色正方形:
2+(a+2)×2=2a+6(个)
答:当中间摆a个灰色的正方形时,四周共需要摆(2a+6)个白色正方形.
故选:A.
12.解:根据图形排列的规律,接着应该摆.
故选:C.
13.解:2012÷5=402…2,
余数是2,所以第2012个图形是一个周期里的第2个图形,即△.
故选:A.
14.解:43÷(2+1+1+1+3),
=43÷8,
=5(个)…3(个),
余数是3,所以排在第43个的是★.
故选:B.
15.解:排列规律是4个图形一组,第1个是正方体,第2个是球,第3个是圆柱,第4个是球,所以按照这个规律接着该摆正方体.
故选:B.
16.解:830÷8=103……6,
可以看出,第830个图形是第104组的第6个图形,是圆.
故选:C.
17.解:三角形的个数依次为:6、9、12……,
可知,前一个图形的三角形数量比后一个少3个,
第5个图形有三角形:
12+3+3
=15+3
=18(个)
故选:C.
18.解:76÷(1+2+3),
=76÷6,
=12…4,
所以第76张纸是第13周期的第4张,是白纸.
故选:C.
三.判断题(共5小题)
19.解:根据以上方向,得:如果把□与△一个隔一个地排成一行,□有15个,△可能有
15个,可能有
14个,也可能有
16个;
所以如果把一个□和一个△一个隔一个地排成一行,有15个□,△最少有15个的说法是错误的;
故答案为:×.
20.解:第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
故答案为:√.
21.解:根据题干分析可得:第n点阵的点数=1+(n﹣1)×4,
n=5时,点数个数为:1+(5﹣1)×4=17.
所以原题说法错误.
故答案为:×.
22.解:57÷6=9…3,
所以第57个图形是第10循环周期的第3个图形,是⊙.
故答案为:√.
23.解:摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
…,
所以摆n个正方形要小棒:4+3×(n﹣1)=3n+1(根);
n=10,3×10+1=31(根);
答:摆10个正方形一共需要31根小棒.
原题说法正确.
故答案为:√.
四.操作题(共3小题)
24.解:
25.解:12÷(8÷2)
=12÷4
=3(份)
答:3份表示12。
如图斜线部分:
。
26.解:
五.应用题(共4小题)
27.解:
掉了
2,3.
故答案为:2,3.
28.解:(1)填表如下:
图序
1
2
3
……
图中黑方块的个数
4
6
8
……
(2)①图1黑色方块4个
图2黑色方块4+2=6(个)
图3黑色方块:4+2+2=8(个)
……
图10黑方块的个数:
2×10+2
=20+2
=22(个)
……
第n个图形黑色方块的个数为:4+2(n﹣1)=(2n+2)个
答:图序为10的图中黑方块有22个;图序为n的图中黑方块有(2n+2)个.
②白方块的排列规律为:
图1:5个
图2:5+3=9(个)
图3:5+3+3=11(个)
……
第n个图形白方块个数:5+3(n﹣1)=(3n+2)个
3n+2=26
3n=24
n=8
答:白方块有26个,这个图的图序为8.
故答案为:6,8;22,(2n+2);8.
29.解:如图:
每3个图形一循环,分别是:、、.
(答案不唯一.)
30.解:(1)每块地砖的边长为:
1.6÷4=0.4(米)
需要地砖的块数:
160×1.6÷0.42
=160×1.6÷0.16
=160×10
=1600(块)
答:铺设这条人行道一共需1600块地砖。
(2)将图形按4×4分组,共有:
160÷16=100(组)
红色地砖有:
100×4=400(块)
答:铺设这条人行道共需要400块红色地砖。
