26.1.2 反比例函数的图像和性质同步练习(含答案)
文档属性
| 名称 | 26.1.2 反比例函数的图像和性质同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 22:58:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十六章 反比例函数
26.1.2 反比例函数的图像和性质练习
一、单选题(共10小题)
1.(2020·兰州市期末)已知反比例函数y=﹣,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y随x的增大而增大;④当x>﹣1时,则y>8.其中错误的结论有( )个
A.3 B.2 C.1 D.0
2.(2020·日照市期中)如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A.4 B.3 C.2 D.1
3.(2020·重庆市期中)若点,,在反比例函数的图像上,则,,的大小关系是( )
A. B. C. D.
4.(2020·贵阳市期末)若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
5.(2020·新余市期中)在反比例函数的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
6.(2020·深圳市期末)若反比例函数y=图象经过点(5,-1),该函数图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
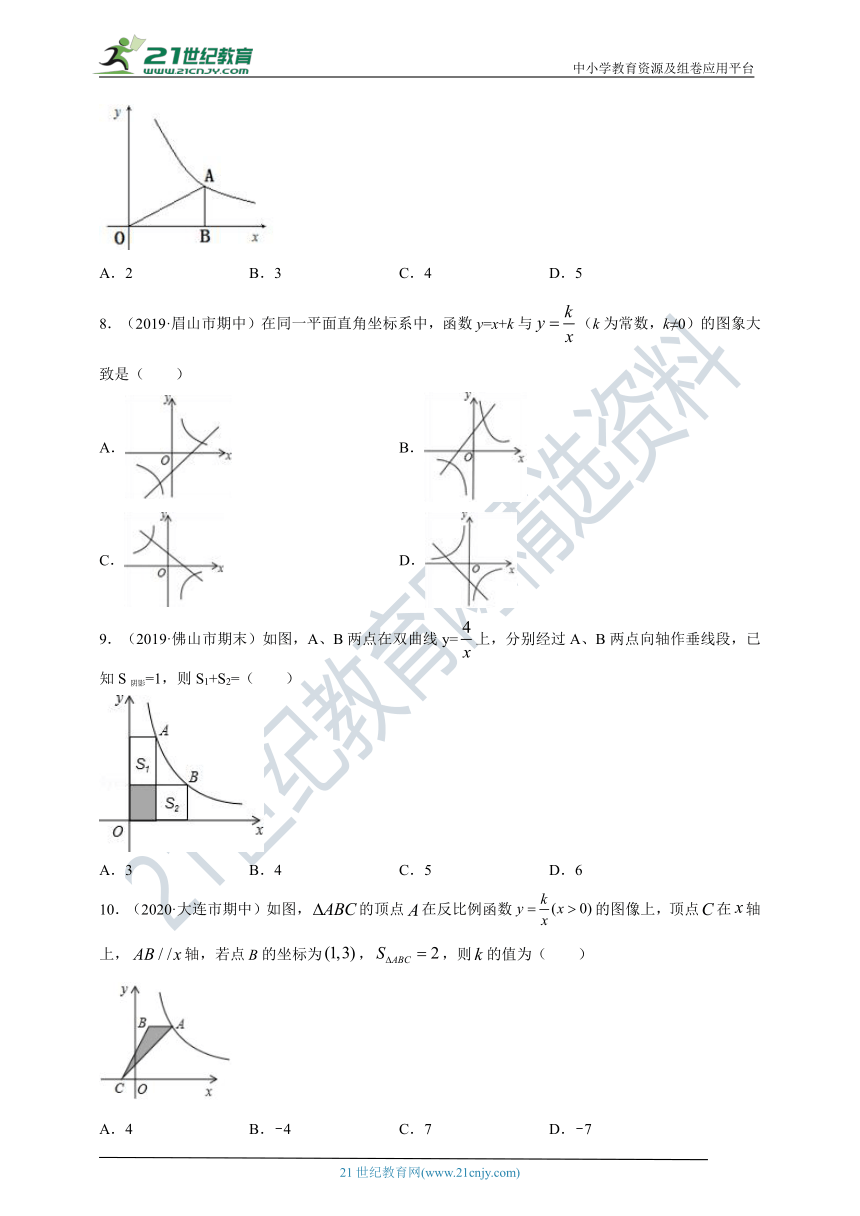
7.(2020·沧州市期末)如图,过反比例函数的图像上一点A作AB⊥轴于点B,连接AO,若S△AOB=2,则的值为( )
A.2 B.3 C.4 D.5
8.(2019·眉山市期中)在同一平面直角坐标系中,函数y=x+k与(k为常数,k≠0)的图象大致是( )
A. B.
C. D.
9.(2019·佛山市期末)如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A.3 B.4 C.5 D.6
10.(2020·大连市期中)如图,的顶点在反比例函数的图像上,顶点在轴上,轴,若点的坐标为,,则的值为( )
A.4 B.-4 C.7 D.-7
二、填空题(共5小题)
11.(2020·洛阳市期中)如图,已知反比例函数y=(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=________________.
12.(2020·邵阳市期末)如图,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为_____.
13.(2019·菏泽市期中)如图,菱形ABCD的面积为6,边AD在x轴上,边BC的中点E在y轴上,反比例函数的图象经过顶点B,则k的值为______.
14.(2020·济南市期中)如图,已知直线y=mx与双曲线y=一个交点坐标为(3,4),则它们的另一个交点坐标是_____.
15.(2018·南宁市期末)对于函数,当函数值y<﹣1时,自变量x的取值范围是 .
三、解 答题(共2小题)
16.(2019·重庆市期末)如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.
17.(2020·大连市期末)如图,已知反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求n和b的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
答案
一、单选题(共10小题)
1.【答案】B
【详解】
①当x=﹣2时,y=4,即图象必经过点(﹣2,4);
②k=﹣8<0,图象在第二、四象限内;
③k=﹣8<0,每一象限内,y随x的增大而增大,错误;
④k=﹣8<0,每一象限内,y随x的增大而增大,若0>x>﹣1,﹣y>8,故④错误,
故选B.
2.【答案】B
【详解】∵A,B是反比例函数y=在第一象限内的图象上的两点,
且A,B两点的横坐标分别是2和4,
∴当x=2时,y=2,即A(2,2),
当x=4时,y=1,即B(4,1),
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,
则S△AOC=S△BOD=×4=2,
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,
∴S△AOB=S梯形ABDC,
∵S梯形ABDC=(BD+AC)?CD=×(1+2)×2=3,
∴S△AOB=3,
故选B.
3.【答案】B
详解:∵反比例函数y=中,k=12>0,
∴此函数的图象在一、三象限,在每一象限内y随x的增大而减小,
∵y1<y2<0<y3,
∴.
故选B.
4.【答案】D
试题分析:反比例函数的图象经过点,求出K=-2,当K>0时反比例函数的图象在第一、三象限,当K〈0时反比例函数的图象在第二、四象限,因为-2〈0,D正确.
故选D
5.【答案】A
【详解】
解:根据题意,在反比例函数图象的每一支曲线上,y都随x的增大而减小,
即可得k﹣1>0,
解得k>1.
故选A.
6.【答案】D
【解析】
∵反比例函数y=的图象经过点(5,-1),
∴k=5×(-1)=-5<0,
∴该函数图象在第二、四象限.
故选D.
7.【答案】C
试题分析:观察图象可得,k>0,已知S△AOB=2,根据反比例函数k的几何意义可得k=4,故答案选C.
8.【答案】B
【详解】
选项A中,由一次函数y=x+k的图象知k<0,由反比例函数y=的图象知k>0,矛盾,所以选项A错误;选项B中,由一次函数y=x+k的图象知k>0,由反比例函数y=的图象知k>0,正确,所以选项B正确;由一次函数y=x+k的图象知,函数图象从左到右上升,所以选项C、D错误.
故选B.
9.【答案】D
【详解】
∵点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,
则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,
∴S1+S2=4+4-1×2=6.
故选D.
10.【答案】C
【详解】
解:∵AB∥x轴,若点B的坐标为(1,3),
∴设点A(a,3)
∵S△ABC=(a-1)×3=2,
∴a=,
∴点A(,3)
∵点A在反比例函数y=(x>0)的图象上,
∴k=7,
故选C.
二、填空题(共5小题)
11.【答案】-2
试题解析:设点A的坐标为(m,n),因为点A在y=的图象上,所以,有mn=k,△ABO的面积为=1,∴=2,∴=2,∴k=±2,由函数图象位于第二、四象限知k<0,∴k=-2.
12.【答案】
设A坐标为(x,y),
∵B(3,-3),C(5,0),以OC,CB为边作平行四边形OABC,
∴x+5=0+3,y+0=0-3,
解得:x=-2,y=-3,即A(-2,-3),
设过点A的反比例解析式为y=,
把A(-2,-3)代入得:k=6,
则过点A的反比例解析式为y=,
故答案为y=.
13.【答案】3
【详解】
在Rt△AEB中,∵∠AEB=90°,AB=2BE,
∴∠EAB=30°,
设AE=a,则AB=2a,由题意2a×a=6,
∴a2=,
∴k=a2=3,
故答案为3.
14.【答案】(﹣3,﹣4)
【详解】
解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,
所以其交点坐标关于原点对称,一个交点坐标为(3,4),则另一个交点的坐标为(﹣3,﹣4).
故答案是:(﹣3,﹣4).
15.(2018·南宁市期末)对于函数,当函数值y<﹣1时,自变量x的取值范围是
【答案】﹣2<x<0.
【解析】
试题分析:∵当y=﹣1时,x=﹣2,∴当函数值y<﹣1时,﹣2<x<0.故答案为:﹣2<x<0.
三、解 答题(共2小题)
16.【答案】(1)y=- (2)点P(﹣6,0)或(﹣2,0)
【详解】
(1)把点A(﹣1,a)代入y=x+4,得a=3,
∴A(﹣1,3)
把A(﹣1,3)代入反比例函数
∴k=﹣3,
∴反比例函数的表达式为
(2)联立两个函数的表达式得
解得
或
∴点B的坐标为B(﹣3,1)
当y=x+4=0时,得x=﹣4
∴点C(﹣4,0)
设点P的坐标为(x,0)
∵,
∴
解得x1=﹣6,x2=﹣2
∴点P(﹣6,0)或(﹣2,0)
17.【答案】(1)-1;(2)7.5;(3)x>1或﹣4<x<0.
【详解】
(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,
得k=1×4,1+b=4,
解得k=4,b=3,
∵点B(﹣4,n)也在反比例函数y=的图象上,
∴n==﹣1;
(2)如图,设直线y=x+3与y轴的交点为C,
∵当x=0时,y=3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC=×3×1+×3×4=7.5,
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
_21?????????è?????(www.21cnjy.com)_
第二十六章 反比例函数
26.1.2 反比例函数的图像和性质练习
一、单选题(共10小题)
1.(2020·兰州市期末)已知反比例函数y=﹣,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y随x的增大而增大;④当x>﹣1时,则y>8.其中错误的结论有( )个
A.3 B.2 C.1 D.0
2.(2020·日照市期中)如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A.4 B.3 C.2 D.1
3.(2020·重庆市期中)若点,,在反比例函数的图像上,则,,的大小关系是( )
A. B. C. D.
4.(2020·贵阳市期末)若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
5.(2020·新余市期中)在反比例函数的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
6.(2020·深圳市期末)若反比例函数y=图象经过点(5,-1),该函数图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
7.(2020·沧州市期末)如图,过反比例函数的图像上一点A作AB⊥轴于点B,连接AO,若S△AOB=2,则的值为( )
A.2 B.3 C.4 D.5
8.(2019·眉山市期中)在同一平面直角坐标系中,函数y=x+k与(k为常数,k≠0)的图象大致是( )
A. B.
C. D.
9.(2019·佛山市期末)如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A.3 B.4 C.5 D.6
10.(2020·大连市期中)如图,的顶点在反比例函数的图像上,顶点在轴上,轴,若点的坐标为,,则的值为( )
A.4 B.-4 C.7 D.-7
二、填空题(共5小题)
11.(2020·洛阳市期中)如图,已知反比例函数y=(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k=________________.
12.(2020·邵阳市期末)如图,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为_____.
13.(2019·菏泽市期中)如图,菱形ABCD的面积为6,边AD在x轴上,边BC的中点E在y轴上,反比例函数的图象经过顶点B,则k的值为______.
14.(2020·济南市期中)如图,已知直线y=mx与双曲线y=一个交点坐标为(3,4),则它们的另一个交点坐标是_____.
15.(2018·南宁市期末)对于函数,当函数值y<﹣1时,自变量x的取值范围是 .
三、解 答题(共2小题)
16.(2019·重庆市期末)如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.
17.(2020·大连市期末)如图,已知反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求n和b的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
答案
一、单选题(共10小题)
1.【答案】B
【详解】
①当x=﹣2时,y=4,即图象必经过点(﹣2,4);
②k=﹣8<0,图象在第二、四象限内;
③k=﹣8<0,每一象限内,y随x的增大而增大,错误;
④k=﹣8<0,每一象限内,y随x的增大而增大,若0>x>﹣1,﹣y>8,故④错误,
故选B.
2.【答案】B
【详解】∵A,B是反比例函数y=在第一象限内的图象上的两点,
且A,B两点的横坐标分别是2和4,
∴当x=2时,y=2,即A(2,2),
当x=4时,y=1,即B(4,1),
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,
则S△AOC=S△BOD=×4=2,
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,
∴S△AOB=S梯形ABDC,
∵S梯形ABDC=(BD+AC)?CD=×(1+2)×2=3,
∴S△AOB=3,
故选B.
3.【答案】B
详解:∵反比例函数y=中,k=12>0,
∴此函数的图象在一、三象限,在每一象限内y随x的增大而减小,
∵y1<y2<0<y3,
∴.
故选B.
4.【答案】D
试题分析:反比例函数的图象经过点,求出K=-2,当K>0时反比例函数的图象在第一、三象限,当K〈0时反比例函数的图象在第二、四象限,因为-2〈0,D正确.
故选D
5.【答案】A
【详解】
解:根据题意,在反比例函数图象的每一支曲线上,y都随x的增大而减小,
即可得k﹣1>0,
解得k>1.
故选A.
6.【答案】D
【解析】
∵反比例函数y=的图象经过点(5,-1),
∴k=5×(-1)=-5<0,
∴该函数图象在第二、四象限.
故选D.
7.【答案】C
试题分析:观察图象可得,k>0,已知S△AOB=2,根据反比例函数k的几何意义可得k=4,故答案选C.
8.【答案】B
【详解】
选项A中,由一次函数y=x+k的图象知k<0,由反比例函数y=的图象知k>0,矛盾,所以选项A错误;选项B中,由一次函数y=x+k的图象知k>0,由反比例函数y=的图象知k>0,正确,所以选项B正确;由一次函数y=x+k的图象知,函数图象从左到右上升,所以选项C、D错误.
故选B.
9.【答案】D
【详解】
∵点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,
则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,
∴S1+S2=4+4-1×2=6.
故选D.
10.【答案】C
【详解】
解:∵AB∥x轴,若点B的坐标为(1,3),
∴设点A(a,3)
∵S△ABC=(a-1)×3=2,
∴a=,
∴点A(,3)
∵点A在反比例函数y=(x>0)的图象上,
∴k=7,
故选C.
二、填空题(共5小题)
11.【答案】-2
试题解析:设点A的坐标为(m,n),因为点A在y=的图象上,所以,有mn=k,△ABO的面积为=1,∴=2,∴=2,∴k=±2,由函数图象位于第二、四象限知k<0,∴k=-2.
12.【答案】
设A坐标为(x,y),
∵B(3,-3),C(5,0),以OC,CB为边作平行四边形OABC,
∴x+5=0+3,y+0=0-3,
解得:x=-2,y=-3,即A(-2,-3),
设过点A的反比例解析式为y=,
把A(-2,-3)代入得:k=6,
则过点A的反比例解析式为y=,
故答案为y=.
13.【答案】3
【详解】
在Rt△AEB中,∵∠AEB=90°,AB=2BE,
∴∠EAB=30°,
设AE=a,则AB=2a,由题意2a×a=6,
∴a2=,
∴k=a2=3,
故答案为3.
14.【答案】(﹣3,﹣4)
【详解】
解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,
所以其交点坐标关于原点对称,一个交点坐标为(3,4),则另一个交点的坐标为(﹣3,﹣4).
故答案是:(﹣3,﹣4).
15.(2018·南宁市期末)对于函数,当函数值y<﹣1时,自变量x的取值范围是
【答案】﹣2<x<0.
【解析】
试题分析:∵当y=﹣1时,x=﹣2,∴当函数值y<﹣1时,﹣2<x<0.故答案为:﹣2<x<0.
三、解 答题(共2小题)
16.【答案】(1)y=- (2)点P(﹣6,0)或(﹣2,0)
【详解】
(1)把点A(﹣1,a)代入y=x+4,得a=3,
∴A(﹣1,3)
把A(﹣1,3)代入反比例函数
∴k=﹣3,
∴反比例函数的表达式为
(2)联立两个函数的表达式得
解得
或
∴点B的坐标为B(﹣3,1)
当y=x+4=0时,得x=﹣4
∴点C(﹣4,0)
设点P的坐标为(x,0)
∵,
∴
解得x1=﹣6,x2=﹣2
∴点P(﹣6,0)或(﹣2,0)
17.【答案】(1)-1;(2)7.5;(3)x>1或﹣4<x<0.
【详解】
(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,
得k=1×4,1+b=4,
解得k=4,b=3,
∵点B(﹣4,n)也在反比例函数y=的图象上,
∴n==﹣1;
(2)如图,设直线y=x+3与y轴的交点为C,
∵当x=0时,y=3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC=×3×1+×3×4=7.5,
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
_21?????????è?????(www.21cnjy.com)_
