27.3 位似同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
27.3 位似练习
一、单选题(共10小题)
1.(2020·洛阳市期中)如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
2.(2020·郑州市期末)如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
3.(2020·平桂区期末)如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
4.(2020·重庆市期末)如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A.或 B.
C. D.或
5.(2018·汶上县期末)在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )
A. B.或
C. D.或
6.(2019·北镇期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2∶1,把△EFO缩小,则点E的对应点E′的坐标是
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
7.(2018·长阳县期末)在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,﹣6),则A点的对应点A′坐标为( )
A.(﹣2,﹣4) B.(﹣4,﹣2)
C.(﹣1,﹣4) D.(1,﹣4)
8.(2018·淄博市期中)如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
A.1:3 B.1:4 C.1:5 D.1:9
9.(2020·保定市期末)图中的两个三角形是位似图形,它们的位似中心是( )
A.点P B.点D
C.点M D.点N
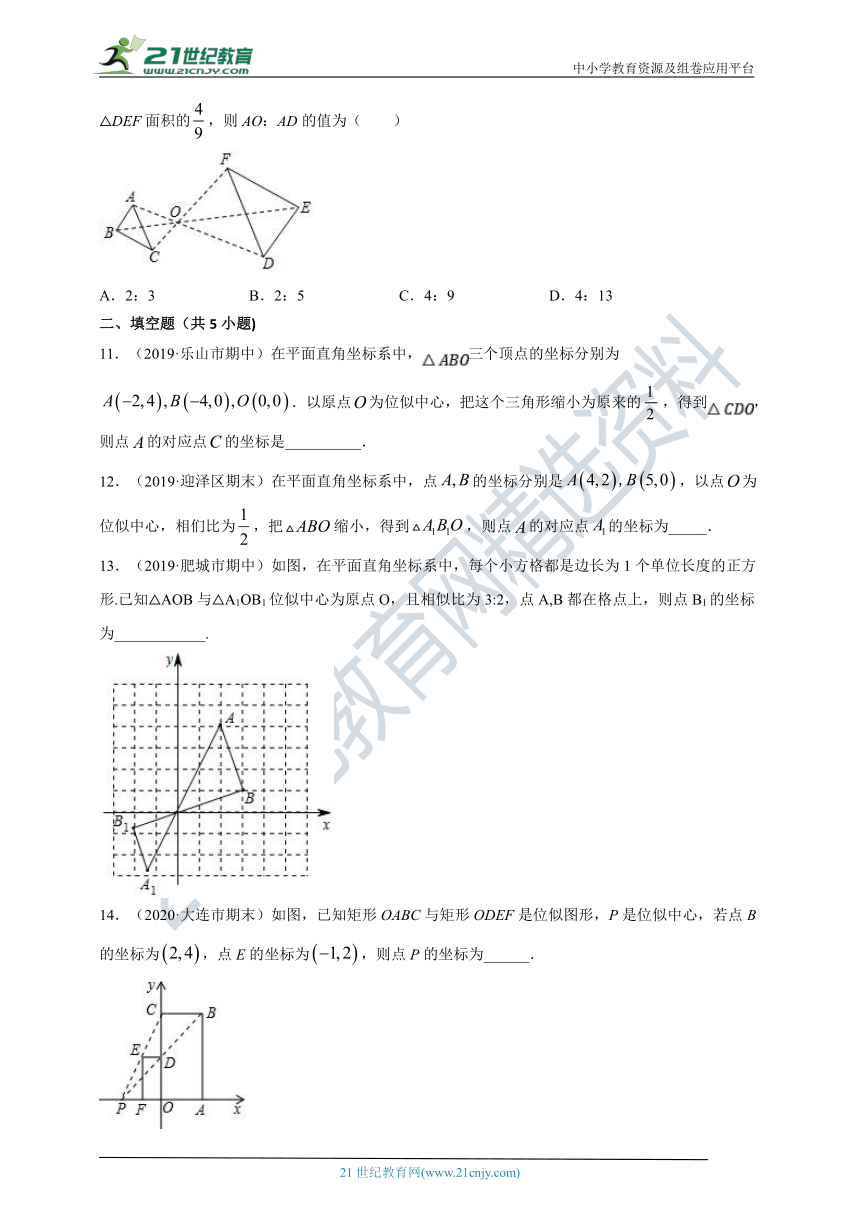
10.(2020·贵阳市期末)如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO:AD的值为( )
A.2:3 B.2:5 C.4:9 D.4:13
二、填空题(共5小题)
11.(2019·乐山市期中)在平面直角坐标系中,三个顶点的坐标分别为.以原点为位似中心,把这个三角形缩小为原来的,得到,则点的对应点的坐标是__________.
12.(2019·迎泽区期末)在平面直角坐标系中,点的坐标分别是,以点为位似中心,相们比为,把缩小,得到,则点的对应点的坐标为_____.
13.(2019·肥城市期中)如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为____________.
14.(2020·大连市期末)如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为,点E的坐标为,则点P的坐标为______.
15.(2020·盐湖区期中)如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是__.
三、解答题(共3小题)
16.(2020·无锡市期中)如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
17.(2019·兰州市期中)如图10,在6×8的网格图中,每个小正方形边长均为1,点
O和△ABC的顶点均为小正方形的顶点.
⑴以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2
⑵连接⑴中的AA′,求四边形AA′C′C的周长.(结果保留根号)
18.(2018·昆明市期末)如图,在方格纸中.
(1)请在方格纸上建立平面直角坐标系,使,,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
(3)计算的面积.
答案
一、单选题(共10小题)
1.(【答案】A
【详解】
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴=,
∵BG=6,
∴AD=BC=2,
∵AD∥BG,
∴△OAD∽△OBG,
∴=,
∴=,
解得:OA=1,∴OB=3,
∴C点坐标为:(3,2),
故选A.
2.【答案】A
【详解】
由题意得,△ODC∽△OBA,相似比是,
∴,
又OB=6,AB=3,
∴OD=2,CD=1,
∴点C的坐标为:(2,1),
故选A.
3.【答案】A
【详解】
由位似变换的性质可知,A′B′∥AB,A′C′∥AC,
∴△A′B′C′∽△ABC,
∵△A'B'C'与△ABC的面积的比4:9,
∴△A'B'C'与△ABC的相似比为2:3,
∴ ,
故选A.
4.【答案】D
【详解】
解:∵以原点O为位似中心,相似比为,把△ABO缩小,
∴点B(-9,-3)的对应点B′的坐标是(-3,-1)或(3,1).
故选D.
5.【解析】
分析:根据位似变换的性质计算即可.
详解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n)或(-2m,-2n),
故选B.
6.【答案】D
【解析】
试题分析:根据位似的性质,缩小后的点在原点的同侧,为(-2,1),然后求在另一侧为(2,-1).
故选D
7.【答案】A
【详解】
解:∵△OA′B′与△OAB关于O(0,0)成位似图形,且若B?(0,3)的对应点B′的坐标为(0,-6),
∴OB:OB'=1:2=OA:OA'
∵A(1,2),
∴A'(-2,-4)
故选A.
8.【答案】D
解:∵OB=3OB′,
∴OB′:OB=1:3,
∵以点O为位似中心,将△ABC缩小后得到△A′B′C′,
∴△A′B′C′∽△ABC,
∴A′B′:AB=OB′:OB=1:3,
∴.
故选D
9.【答案】A
解:∵位似图形的位似中心位于对应点连线所在的直线上,点M、N为对应点,所以位似中心在M、N所在的直线上,
因为点P在直线MN上,
所以点P为位似中心.
故选A.
10.【答案】B
O是位似中心,根据位似图形的性质得到AB:DO═2:3,进而得出答案.
【详解】
∵△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,
∴=,AC∥DF,
∴==,
∴=.
故选:B.
二、填空题(共5小题)
11.【答案】或
【详解】
解:以原点为位似中心,把这个三角形缩小为原来的,点的坐标为,
∴点的坐标为或,即或,
故答案为或.
12.【答案】或
【详解】
解:以点为位似中心,相似比为,把缩小,点的坐标是
则点的对应点的坐标为或,即或,
故答案为:或.
13.【答案】
【详解】
由图象可知点B的坐标为(3,1),
∵△AOB与△A1OB1位似中心为原点O,且相似比为3:2,
∴点B1的坐标为[3× ,1×],
即点B1的坐标为(-2,).
故答案为:(-2,).
14.【答案】?
详解:∵四边形OABC是矩形,点B的坐标为(2,4), ∴OC=AB=4,OA=2,
∴点C的坐标为:(0,4),
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2),
∴位似比为:2, ∴OP:AP=OD:AB=1:2, 设OP=x,则, 解得:x=2,
∴OP=2, 即点P的坐标为:(-2,0).
15.【答案】(9,0)
【详解】
根据位似图形的定义,连接A′A,B′B并延长交于(9,0),
所以位似中心的坐标为(9,0).
故答案为:(9,0).
三、解答题(共3小题)
16.【答案】(1)见解析(2)
试题解析:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,由图形可知,∠A2C2B2=∠ACB,过点A作AD⊥BC交BC的延长线于点D,由A(2,2),C(4,﹣4),B(4,0),易得D(4,2),故AD=2,CD=6,AC==,∴sin∠ACB===,即sin∠A2C2B2=.
17.【答案】解:⑴如图1.
⑵
在⊿中,=2,得;于是,
∴四边形的周长=
【解析】
(2)AA′=1,CC′=2.
在Rt△OA′C′中,
OA′=1,OC′=2,得A′C′=,;
同理可得AC=.
∴四边形AA′C′C的周长=3+
18.【答案】(1)作图见解析;.(2)作图见解析;(3)16.
详解:(1)如图所示,即为所求的直角坐标系;B(2,1);
(2)如图:△A'B'C'即为所求;
(3)S△A'B'C'=×4×8=16.
_21?????????è?????(www.21cnjy.com)_
27.3 位似练习
一、单选题(共10小题)
1.(2020·洛阳市期中)如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
2.(2020·郑州市期末)如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
3.(2020·平桂区期末)如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
4.(2020·重庆市期末)如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A.或 B.
C. D.或
5.(2018·汶上县期末)在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )
A. B.或
C. D.或
6.(2019·北镇期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2∶1,把△EFO缩小,则点E的对应点E′的坐标是
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
7.(2018·长阳县期末)在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,﹣6),则A点的对应点A′坐标为( )
A.(﹣2,﹣4) B.(﹣4,﹣2)
C.(﹣1,﹣4) D.(1,﹣4)
8.(2018·淄博市期中)如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
A.1:3 B.1:4 C.1:5 D.1:9
9.(2020·保定市期末)图中的两个三角形是位似图形,它们的位似中心是( )
A.点P B.点D
C.点M D.点N
10.(2020·贵阳市期末)如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO:AD的值为( )
A.2:3 B.2:5 C.4:9 D.4:13
二、填空题(共5小题)
11.(2019·乐山市期中)在平面直角坐标系中,三个顶点的坐标分别为.以原点为位似中心,把这个三角形缩小为原来的,得到,则点的对应点的坐标是__________.
12.(2019·迎泽区期末)在平面直角坐标系中,点的坐标分别是,以点为位似中心,相们比为,把缩小,得到,则点的对应点的坐标为_____.
13.(2019·肥城市期中)如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为____________.
14.(2020·大连市期末)如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为,点E的坐标为,则点P的坐标为______.
15.(2020·盐湖区期中)如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是__.
三、解答题(共3小题)
16.(2020·无锡市期中)如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
17.(2019·兰州市期中)如图10,在6×8的网格图中,每个小正方形边长均为1,点
O和△ABC的顶点均为小正方形的顶点.
⑴以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2
⑵连接⑴中的AA′,求四边形AA′C′C的周长.(结果保留根号)
18.(2018·昆明市期末)如图,在方格纸中.
(1)请在方格纸上建立平面直角坐标系,使,,并求出点坐标;
(2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形;
(3)计算的面积.
答案
一、单选题(共10小题)
1.(【答案】A
【详解】
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴=,
∵BG=6,
∴AD=BC=2,
∵AD∥BG,
∴△OAD∽△OBG,
∴=,
∴=,
解得:OA=1,∴OB=3,
∴C点坐标为:(3,2),
故选A.
2.【答案】A
【详解】
由题意得,△ODC∽△OBA,相似比是,
∴,
又OB=6,AB=3,
∴OD=2,CD=1,
∴点C的坐标为:(2,1),
故选A.
3.【答案】A
【详解】
由位似变换的性质可知,A′B′∥AB,A′C′∥AC,
∴△A′B′C′∽△ABC,
∵△A'B'C'与△ABC的面积的比4:9,
∴△A'B'C'与△ABC的相似比为2:3,
∴ ,
故选A.
4.【答案】D
【详解】
解:∵以原点O为位似中心,相似比为,把△ABO缩小,
∴点B(-9,-3)的对应点B′的坐标是(-3,-1)或(3,1).
故选D.
5.【解析】
分析:根据位似变换的性质计算即可.
详解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n)或(-2m,-2n),
故选B.
6.【答案】D
【解析】
试题分析:根据位似的性质,缩小后的点在原点的同侧,为(-2,1),然后求在另一侧为(2,-1).
故选D
7.【答案】A
【详解】
解:∵△OA′B′与△OAB关于O(0,0)成位似图形,且若B?(0,3)的对应点B′的坐标为(0,-6),
∴OB:OB'=1:2=OA:OA'
∵A(1,2),
∴A'(-2,-4)
故选A.
8.【答案】D
解:∵OB=3OB′,
∴OB′:OB=1:3,
∵以点O为位似中心,将△ABC缩小后得到△A′B′C′,
∴△A′B′C′∽△ABC,
∴A′B′:AB=OB′:OB=1:3,
∴.
故选D
9.【答案】A
解:∵位似图形的位似中心位于对应点连线所在的直线上,点M、N为对应点,所以位似中心在M、N所在的直线上,
因为点P在直线MN上,
所以点P为位似中心.
故选A.
10.【答案】B
O是位似中心,根据位似图形的性质得到AB:DO═2:3,进而得出答案.
【详解】
∵△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,
∴=,AC∥DF,
∴==,
∴=.
故选:B.
二、填空题(共5小题)
11.【答案】或
【详解】
解:以原点为位似中心,把这个三角形缩小为原来的,点的坐标为,
∴点的坐标为或,即或,
故答案为或.
12.【答案】或
【详解】
解:以点为位似中心,相似比为,把缩小,点的坐标是
则点的对应点的坐标为或,即或,
故答案为:或.
13.【答案】
【详解】
由图象可知点B的坐标为(3,1),
∵△AOB与△A1OB1位似中心为原点O,且相似比为3:2,
∴点B1的坐标为[3× ,1×],
即点B1的坐标为(-2,).
故答案为:(-2,).
14.【答案】?
详解:∵四边形OABC是矩形,点B的坐标为(2,4), ∴OC=AB=4,OA=2,
∴点C的坐标为:(0,4),
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2),
∴位似比为:2, ∴OP:AP=OD:AB=1:2, 设OP=x,则, 解得:x=2,
∴OP=2, 即点P的坐标为:(-2,0).
15.【答案】(9,0)
【详解】
根据位似图形的定义,连接A′A,B′B并延长交于(9,0),
所以位似中心的坐标为(9,0).
故答案为:(9,0).
三、解答题(共3小题)
16.【答案】(1)见解析(2)
试题解析:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,由图形可知,∠A2C2B2=∠ACB,过点A作AD⊥BC交BC的延长线于点D,由A(2,2),C(4,﹣4),B(4,0),易得D(4,2),故AD=2,CD=6,AC==,∴sin∠ACB===,即sin∠A2C2B2=.
17.【答案】解:⑴如图1.
⑵
在⊿中,=2,得;于是,
∴四边形的周长=
【解析】
(2)AA′=1,CC′=2.
在Rt△OA′C′中,
OA′=1,OC′=2,得A′C′=,;
同理可得AC=.
∴四边形AA′C′C的周长=3+
18.【答案】(1)作图见解析;.(2)作图见解析;(3)16.
详解:(1)如图所示,即为所求的直角坐标系;B(2,1);
(2)如图:△A'B'C'即为所求;
(3)S△A'B'C'=×4×8=16.
_21?????????è?????(www.21cnjy.com)_
