人教版七年级数学2019-2020学年第二学期5.2平行线及其判定过关训练(word版含简单答案)
文档属性
| 名称 | 人教版七年级数学2019-2020学年第二学期5.2平行线及其判定过关训练(word版含简单答案) |  | |
| 格式 | zip | ||
| 文件大小 | 312.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 22:10:06 | ||
图片预览


文档简介
人教版七年级数学2019-2020学年第二学期第五章相交线与平行线
第2节平行线及其判定过关训练
一、单选题
1.同一平面内,两条直线的位置关系有(
)
A.相交、垂直
B.相交、平行
C.垂直、平行
D.相交、垂直、平行
2.如图,不一定能推出a∥b的条件是(
)
A.∠1=∠3
B.∠2=∠4
C.∠1=∠4
D.∠2+∠3=180?
3.已知在同一平面内三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是(
)
A.a⊥b
B.a⊥b或a∥b
C.a∥b
D.无法确定
4.如图,下列能判定AB∥CD的条件的个数是( )
①∠B+∠BCD=180°;②∠2=∠3;③∠1=∠4;④∠B=∠5.
A.1个
B.2个
C.3个
D.4个
5.如图,下列给出的条件中,能判定AC∥DE的是(
)
A.∠A+∠2=180°
B.∠1=∠A
C.∠1=∠4
D.∠A=∠3
6.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.
则下列判断正确的是(
)
A.纸带①的边线平行,纸带②的边线不平行
B.纸带①、②的边线都平行
C.纸带①的边线不平行,纸带②的边线平行
D.纸带①、②的边线都不平行
8.若a⊥b,c⊥d,则a与c的关系是( )
A.平行
B.垂直
C.相交
D.以上都不对
9.正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为.现有格点,那么,在网格图中找出格点,使以和格点为顶点的三角形的面积为.这样的点可找到的个数为(
)
A.
B.
C.
D.
10.如图,给出下面的推理:①因为,所以;②因为,所以③因为,所以;④因为,所以.其中正确的推理是(
)
A.①②③
B.①②④
C.①③④
D.②③④
二、填空题
11.如图,如果直线AB⊥直线l,直线BC⊥直线l,那么AB与BC重合,其理由是_______.
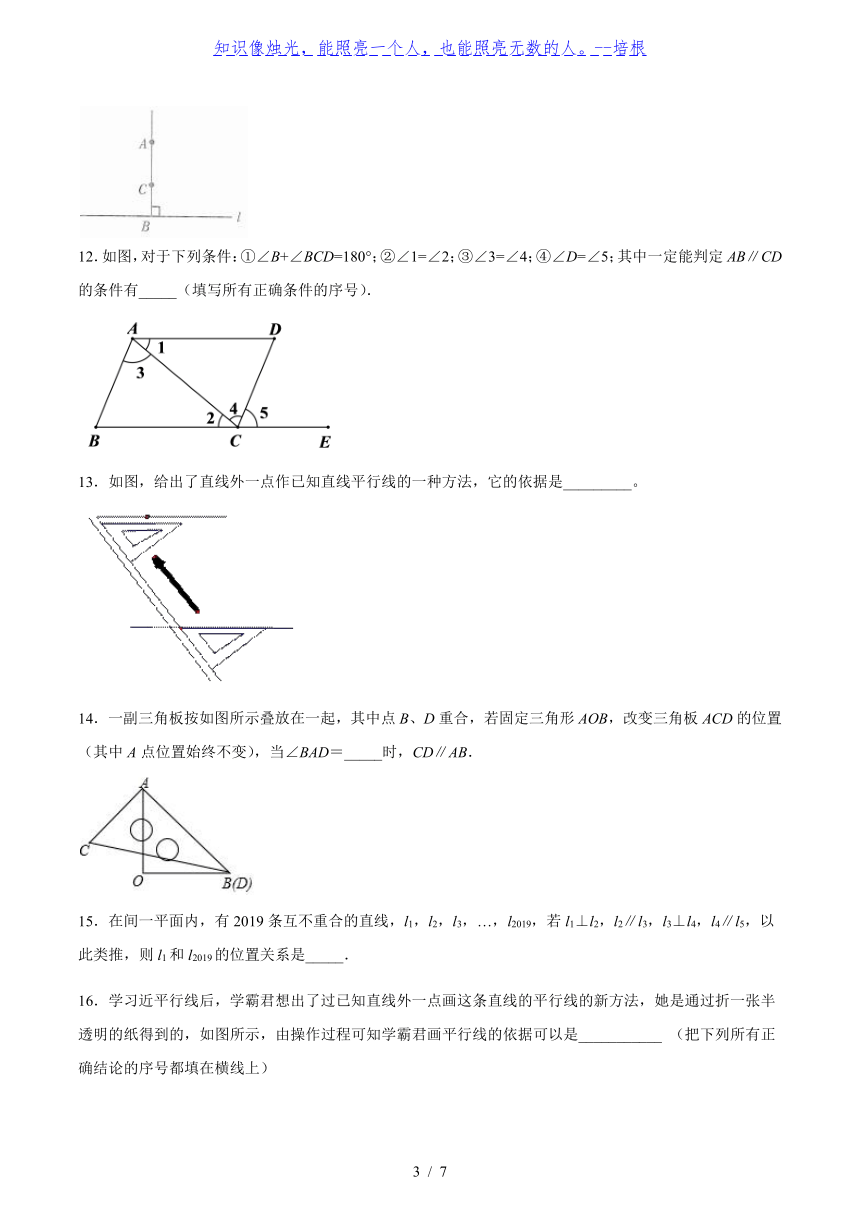
12.如图,对于下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5;其中一定能判定AB∥CD的条件有_____(填写所有正确条件的序号).
13.如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是_________。
14.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD=_____时,CD∥AB.
15.在间一平面内,有2019条互不重合的直线,l1,l2,l3,…,l2019,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5,以此类推,则l1和l2019的位置关系是_____.
16.学习近平行线后,学霸君想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知学霸君画平行线的依据可以是___________
(把下列所有正确结论的序号都填在横线上)
①两直线平行,同位角相等;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
三、解答题
17.如图,已知:∠1=∠2,∠3=108°,求∠4的度数.
18.如图,由相同边长的小正方形组成的网格图形,、、都在格点上,利用网格画图.
(1)过点画的平行线,标出点;
(2)过点画的垂线,垂足为点,标出点;
(3)点到的距离是线段
的长度;
(4)线段、的大小关系为:
(填“”、“”或“”).
19.已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点且∠1+∠2=90°.求证:DE∥BC.
20.如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB=
(
)
∴∠ABD+∠CDB=180°
∴AB∥
(
)
又∠A与∠AEF互补
(
)
∠A+∠AEF=
∴AB∥
(
)
∴CD∥EF
(
)
21.作图题:如图,在平面内有不共线的3个点A,B,C.
(1)作射线BA,在BA延长线上取一点E,使AE=AB;
(2)作线段BC并延长BC到点F,使CF=BC;
(3)连接AC,EF;
(4)度量线段AC和EF的长度,直接写出二者之间的数量关系_______,观察AC和FE的位置是
(填“平行”或“相交”)关系;
(5)作BC的中点D,连接AD,猜想S三角形ABD
S三角形ACD(填“>”“=”或“<”).
22.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
23.阅读材料:
如图1,点是直线上一点,上方的四边形中,,延长,,探究与的数量关系,并证明.
小白的想法是:“作(如图2),通过推理可以得到,从而得出结论”.
请按照小白的想法完成解答:
拓展延伸:
保留原题条件不变,平分,反向延长,交的平分线于点(如图3),设,请直接写出的度数(用含的式子表示).
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
/
参考答案
1.B2.C3.C4.B5.B6.C8.D9.C10.B
11.在同一平面内,过一点有且只有一条直线与已知直线垂直
12.①③
13.同位角相等,两直线平行
14.150°或30°.
15.l1⊥l2019.
16.②③④
17.72°
18.(1)略;(2)略;(3);(4).
19.略
20.90°;垂直的定义;CD;同旁内角互补,两直线平行;已知;180°;EF;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
21.(1)略;(2)略;(3)略;(4)AC=EF(或EF=2AC),平行;(5)=
22.(1);(2)135°;(3)等于或时,.
23.阅读材料:;拓展延伸:.
第2节平行线及其判定过关训练
一、单选题
1.同一平面内,两条直线的位置关系有(
)
A.相交、垂直
B.相交、平行
C.垂直、平行
D.相交、垂直、平行
2.如图,不一定能推出a∥b的条件是(
)
A.∠1=∠3
B.∠2=∠4
C.∠1=∠4
D.∠2+∠3=180?
3.已知在同一平面内三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是(
)
A.a⊥b
B.a⊥b或a∥b
C.a∥b
D.无法确定
4.如图,下列能判定AB∥CD的条件的个数是( )
①∠B+∠BCD=180°;②∠2=∠3;③∠1=∠4;④∠B=∠5.
A.1个
B.2个
C.3个
D.4个
5.如图,下列给出的条件中,能判定AC∥DE的是(
)
A.∠A+∠2=180°
B.∠1=∠A
C.∠1=∠4
D.∠A=∠3
6.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.
则下列判断正确的是(
)
A.纸带①的边线平行,纸带②的边线不平行
B.纸带①、②的边线都平行
C.纸带①的边线不平行,纸带②的边线平行
D.纸带①、②的边线都不平行
8.若a⊥b,c⊥d,则a与c的关系是( )
A.平行
B.垂直
C.相交
D.以上都不对
9.正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为.现有格点,那么,在网格图中找出格点,使以和格点为顶点的三角形的面积为.这样的点可找到的个数为(
)
A.
B.
C.
D.
10.如图,给出下面的推理:①因为,所以;②因为,所以③因为,所以;④因为,所以.其中正确的推理是(
)
A.①②③
B.①②④
C.①③④
D.②③④
二、填空题
11.如图,如果直线AB⊥直线l,直线BC⊥直线l,那么AB与BC重合,其理由是_______.
12.如图,对于下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5;其中一定能判定AB∥CD的条件有_____(填写所有正确条件的序号).
13.如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是_________。
14.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD=_____时,CD∥AB.
15.在间一平面内,有2019条互不重合的直线,l1,l2,l3,…,l2019,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5,以此类推,则l1和l2019的位置关系是_____.
16.学习近平行线后,学霸君想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知学霸君画平行线的依据可以是___________
(把下列所有正确结论的序号都填在横线上)
①两直线平行,同位角相等;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
三、解答题
17.如图,已知:∠1=∠2,∠3=108°,求∠4的度数.
18.如图,由相同边长的小正方形组成的网格图形,、、都在格点上,利用网格画图.
(1)过点画的平行线,标出点;
(2)过点画的垂线,垂足为点,标出点;
(3)点到的距离是线段
的长度;
(4)线段、的大小关系为:
(填“”、“”或“”).
19.已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点且∠1+∠2=90°.求证:DE∥BC.
20.如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB=
(
)
∴∠ABD+∠CDB=180°
∴AB∥
(
)
又∠A与∠AEF互补
(
)
∠A+∠AEF=
∴AB∥
(
)
∴CD∥EF
(
)
21.作图题:如图,在平面内有不共线的3个点A,B,C.
(1)作射线BA,在BA延长线上取一点E,使AE=AB;
(2)作线段BC并延长BC到点F,使CF=BC;
(3)连接AC,EF;
(4)度量线段AC和EF的长度,直接写出二者之间的数量关系_______,观察AC和FE的位置是
(填“平行”或“相交”)关系;
(5)作BC的中点D,连接AD,猜想S三角形ABD
S三角形ACD(填“>”“=”或“<”).
22.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
23.阅读材料:
如图1,点是直线上一点,上方的四边形中,,延长,,探究与的数量关系,并证明.
小白的想法是:“作(如图2),通过推理可以得到,从而得出结论”.
请按照小白的想法完成解答:
拓展延伸:
保留原题条件不变,平分,反向延长,交的平分线于点(如图3),设,请直接写出的度数(用含的式子表示).
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
/
参考答案
1.B2.C3.C4.B5.B6.C8.D9.C10.B
11.在同一平面内,过一点有且只有一条直线与已知直线垂直
12.①③
13.同位角相等,两直线平行
14.150°或30°.
15.l1⊥l2019.
16.②③④
17.72°
18.(1)略;(2)略;(3);(4).
19.略
20.90°;垂直的定义;CD;同旁内角互补,两直线平行;已知;180°;EF;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
21.(1)略;(2)略;(3)略;(4)AC=EF(或EF=2AC),平行;(5)=
22.(1);(2)135°;(3)等于或时,.
23.阅读材料:;拓展延伸:.
