2020-2021学年八年级数学下册 17.1 勾股定理 第1课时 课件(24张)
文档属性
| 名称 | 2020-2021学年八年级数学下册 17.1 勾股定理 第1课时 课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 266.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-14 23:22:54 | ||
图片预览





文档简介
人教版
勾股定理
第1课时
勾股定理习题练习
如果直角三角形的两直角边长分别是a,b,斜边长为c,那么____________________,即直角三角形中两直角边的平方和等于斜边的平方.
a2+b2=c2
基础知识检测
a
b
c
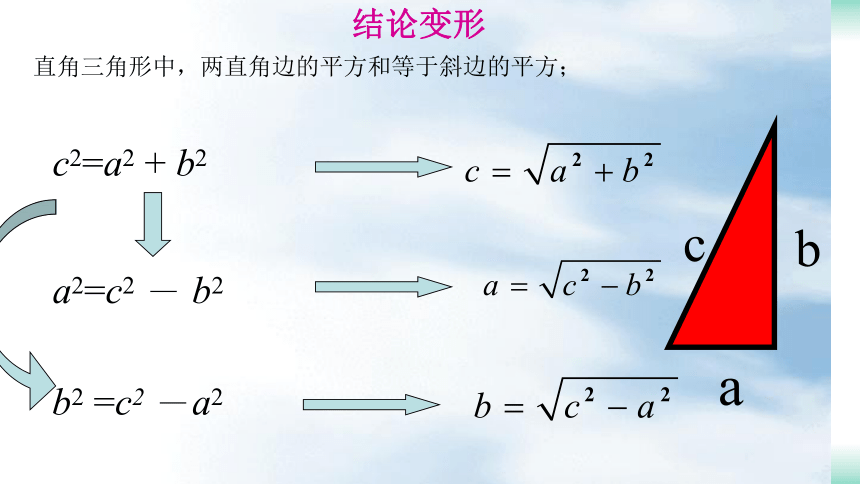
c2=a2 + b2
a2=c2 - b2
b2 =c2 -a2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
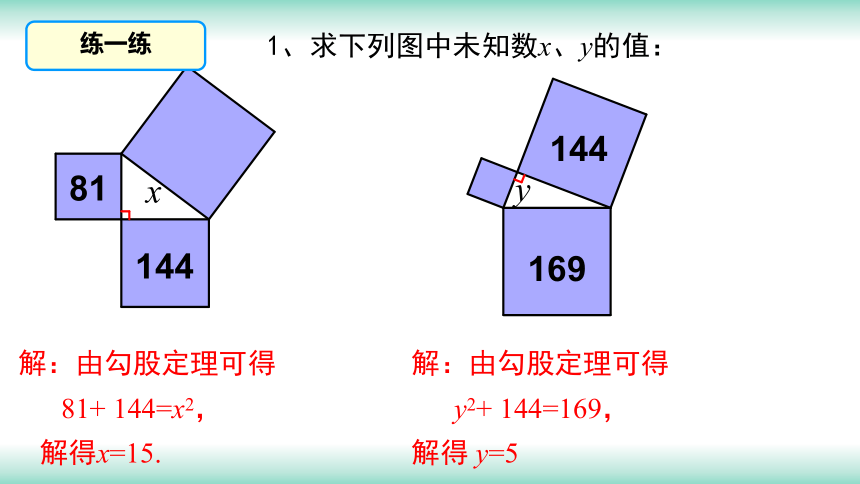
练一练
1、求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144=x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5
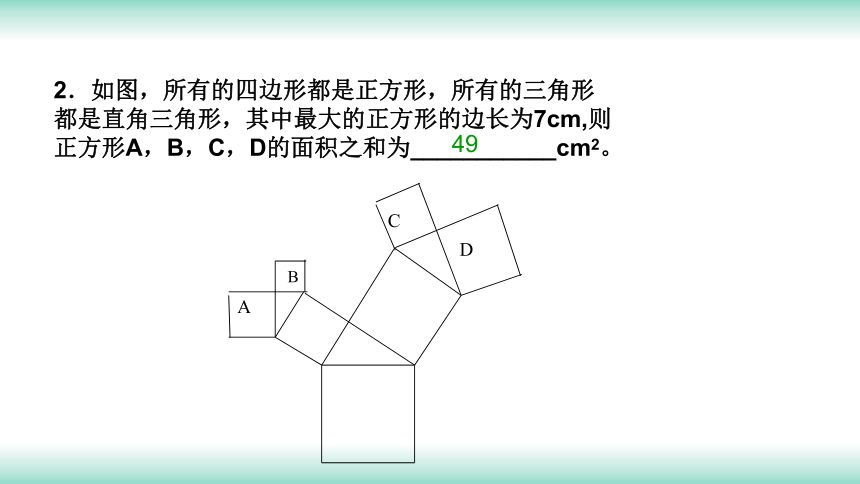
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
A
B
C
D
3、 在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
方法小结
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
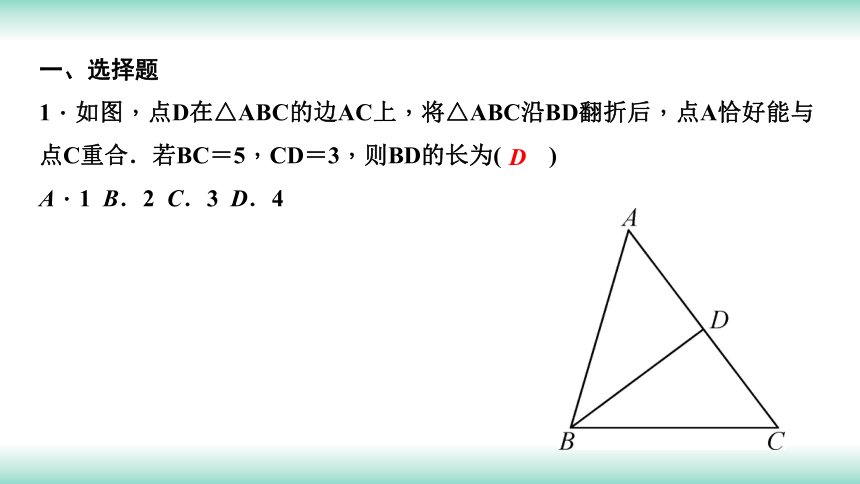
一、选择题
1.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好能与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
D
2.下列说法正确的是( )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
D
3.在直角三角形中,若勾为3,股为4,则弦为( )
A.5 B.6 C.7 D.8
4.已知一个直角三角形三边的平方和为1 800,则斜边长为( )
A.80 B.30 C.90 D.20
A
B
A
6.如图,在Rt△ABC中,∠ACB=90°,AB=15,则两个正方形的面积和为( )
A.225 B.200
C.150 D.无法确定
A
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
D
5
10.在? ABC中, ∠C=90°,AC=6,CB=8,则
?ABC面积为_____,斜边为上的高为______.
24
4.8
A
B
D
c
c
C
11.在Rt△ABC中,若a=5,b=12, 则c =___________.
分析:当c是斜边时, c2= a2+b2
当b是斜边时, b2= a2+c2
13或√119
12.在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=____.
3
14.利用如图(1)或(2)所示的两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为____________,该定理的结论的数学表达式是________________.
勾股定理
a2+b2=c2
16.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=32,求a,c的值.
课堂小结
勾股定理:
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a?+b?=c?.
公式变形:
注意:
1、在直角三角形中
2、看清哪个角是直角
3、已知两边没有指明是直角边还是斜边时一定要分类讨论
谢谢观看
勾股定理
第1课时
勾股定理习题练习
如果直角三角形的两直角边长分别是a,b,斜边长为c,那么____________________,即直角三角形中两直角边的平方和等于斜边的平方.
a2+b2=c2
基础知识检测
a
b
c
c2=a2 + b2
a2=c2 - b2
b2 =c2 -a2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
练一练
1、求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144=x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
A
B
C
D
3、 在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
方法小结
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
一、选择题
1.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好能与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
D
2.下列说法正确的是( )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
D
3.在直角三角形中,若勾为3,股为4,则弦为( )
A.5 B.6 C.7 D.8
4.已知一个直角三角形三边的平方和为1 800,则斜边长为( )
A.80 B.30 C.90 D.20
A
B
A
6.如图,在Rt△ABC中,∠ACB=90°,AB=15,则两个正方形的面积和为( )
A.225 B.200
C.150 D.无法确定
A
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
D
5
10.在? ABC中, ∠C=90°,AC=6,CB=8,则
?ABC面积为_____,斜边为上的高为______.
24
4.8
A
B
D
c
c
C
11.在Rt△ABC中,若a=5,b=12, 则c =___________.
分析:当c是斜边时, c2= a2+b2
当b是斜边时, b2= a2+c2
13或√119
12.在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=____.
3
14.利用如图(1)或(2)所示的两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为____________,该定理的结论的数学表达式是________________.
勾股定理
a2+b2=c2
16.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=32,求a,c的值.
课堂小结
勾股定理:
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a?+b?=c?.
公式变形:
注意:
1、在直角三角形中
2、看清哪个角是直角
3、已知两边没有指明是直角边还是斜边时一定要分类讨论
谢谢观看
