2020-2021学年八年级数学人教版 下册 课时训练 18.1 平行四边形(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版 下册 课时训练 18.1 平行四边形(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 496.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览



文档简介
人教版 八年级下册数学 课时训练 18.1 平行四边形
一、选择题
1. 如图,在平行四边形中,,,平分交边于点,则线段,的长度分别为( )
A.和 B.和 C.和 D.和如图
2. 如图,将?ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
3. 点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有( )种
A. B. C. D.
4. 如图,平行四边形ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( )
A. 3 cm B. 4 cm C. 5 cm D. 8 cm
5. 如图,在△ABC中,AB=4,BC=6,DE、DF是△ABC的中位线,则四边形BEDF的周长是( )
A. 5 B. 7 C. 8 D. 10
6. 如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
7. (2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
8. 已知四边形的四条边长分别是,其中为对边,并且满足
则这个四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.对角线垂直的四边形
二、填空题
9. (2020·牡丹江)如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件__________________,使四边形ABCD是平行四边形(填一个即可).
10. (2020·武汉)在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是□ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是____________.
11. 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.
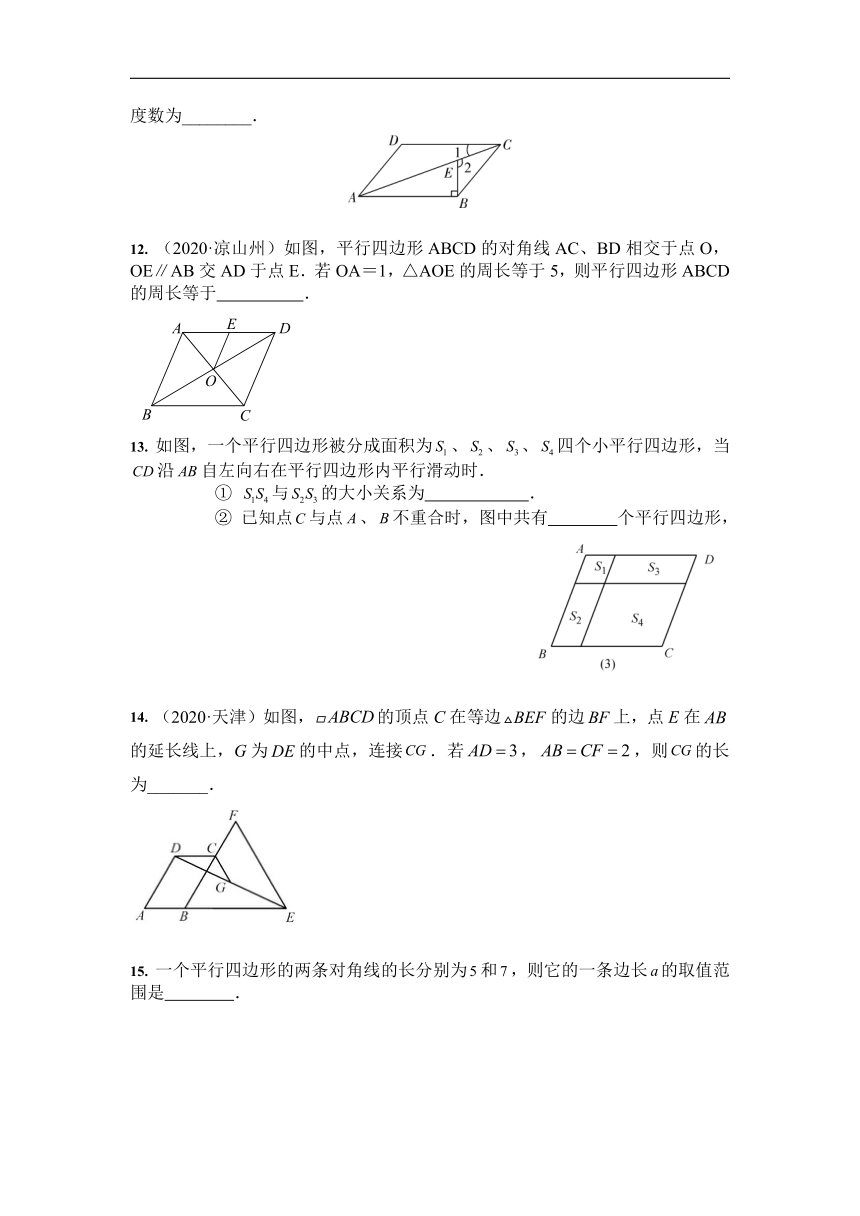
12. (2020·凉山州)如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=1,△AOE的周长等于5,则平行四边形ABCD的周长等于 .
13. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
14. (2020·天津)如图,的顶点C在等边的边上,点E在的延长线上,G为的中点,连接.若,,则的长为_______.
15. 一个平行四边形的两条对角线的长分别为和,则它的一条边长的取值范围是 .
16. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
三、解答题
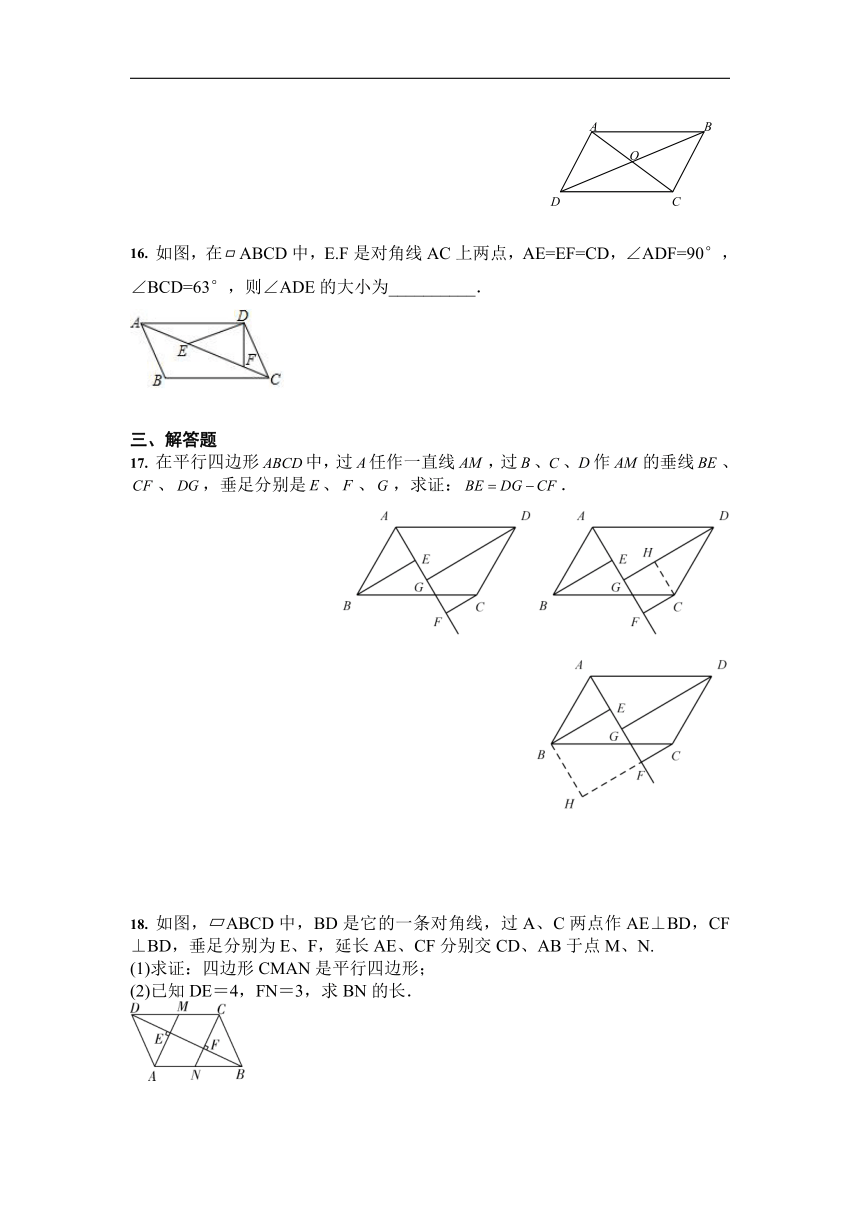
17. 在平行四边形中,过任作一直线,过、、作的垂线、、,垂足分别是、、,求证:.
18. 如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点M、N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求BN的长.
19. 已知:如图,平行四边形中,分别平分、、、,的延长线分别交于点.连接,若,.求的长.
20. 如图,将?ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
人教版 八年级下册数学 课时训练 18.1 平行四边形-答案
一、选择题
1. 【答案】B
2. 【答案】C 【解析】设∠ACD =x,∠B=y,则根据题意可列方程组,解得y=114°.
3. 【答案】B
4. 【答案】B 【解析】在?ABCD中,AD=BC,AB=CD,BO=DO,∵平行四边形ABCD的周长为26 cm,∴AB+BC=13 cm,又∵△AOD的周长比△AOB的周长多3 cm,∴AD-AB=BC-AB=3 cm,解得AB=5 cm,BC=8 cm,又AB⊥AC,E是BC的中点,∴AE=BE=CE=BC=4 cm.
5. 【答案】D 【解析】∵DE、DF是△ABC的中位线,∴DE∥AB,DF∥BC,DE=AB,DF=BC,∴四边形BEDF是平行四边形,∵AB=4,BC=6,∴DE=BF=2,DF=BE=3,∴四边形BEDF的周长为:2(DE+DF)=10.
6. 【答案】C
7. 【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
8. 【答案】B
二、填空题
9. 【答案】AD=BC
【解析】当添加条件AD=BC时,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD是平行四边形.
10. 【答案】26°
【解析】本题考查了等腰三角形性质,平行四边形性质等,∵□ABCD,∴AD=BC,AD∥BC,DC∥AB,又∵AD=AE=BE,∴BC=AE=BE,∴∠BAC=∠EBA,∠BEC=∠BCE,∵AD∥BC,DC∥AB,∴∠DCB=78°,∠BAC=∠DCA,∵∠BEC=∠BAC+∠EBA,∴∠BCE=2∠BAC,∴3∠BAC=78°,解得∠BAC=26°,因此本题答案为26°.
11. 【答案】110° 【解析】 ∵四边形ABCD是平行四边形,∴CD∥AB,∴∠CAB=∠1=20°,∵BE ⊥AB交对角线AC于点E,∴∠ABE=90°,∴∠2=∠CAB+∠ABE=20°+90°=110°.
12. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC.∵OE∥AB,∴OE是△ACD的中位线.∴AE=AD,OE=CD.∵OA=1,△AOE的周长等于5,∴AE+OE=4.∴AD+CD=8.∴平行四边形ABCD的周长=16.故答案为16.
13. 【答案】①;②
14. 【答案】
【解析】本题考查了平行四边形的性质、等边三角形的性质、中位线等知识点,延长DC交EF于点M,利用平行四边形、等边三角形性质求出相应的线段长,证出是的中位线是解题的关键.延长DC交EF于点M(图见详解),根据平行四边形与等边三角形的性质,可证△CFM是等边三角形,BF=BE=EF=BC+CF=5,可求出CF=CM=MF=2,可得C、G是DM和DE的中点,根据中位线的性质,可得出CG=,代入数值即可得出答案.如下图所示,延长DC交EF于点M,,,
平行四边形的顶点C在等边的边上,
,
是等边三角形,
.
在平行四边形中,,,
又是等边三角形,
,
.
G为的中点,,
是的中点,且是的中位线,
.
故答案为:.
15. 【答案】
【解析】如图,不妨设,,,在中,
,,由三角形三边关系可得
,即.
16. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
三、解答题
17. 【答案】
解法一:如图,过作于,则为矩形.
∴,.
又,∴.
又,∴.
∴,∴.
解法二:如图,延长到,使,连接,显然为矩形.
∴.
∵,,∴.
又∵,∴,∴.
∴.
18. 【答案】
(1)证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN,(1分)
又∵四边形ABCD是平行四边形,
∴MC∥AN,
∴四边形CMAN是平行四边形.(2分)
(2)解:∵四边形ABCD是平行四边形,
∴∠ADE=∠CBF,AD=CB,
又∵∠AED=∠CFB=90°,
∴△AED≌△CFB(AAS),(4分)
∴DE=BF=4,
∴在Rt△BFN中,BN==5.(5分)
19. 【答案】
∵四边形是平行四边形,∴,,,
∴,
∵平分,∴,∴,
∴.
∵平分,∴.
同理,,,
∴,∴,即,
∴四边形是平行四边形,∴,,
∴,,
∴四边形是平行四边形,
∴,∴.
20. 【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥FC.(2分)
∵F是BC的中点,
∴FC=BC=AD,
∵DE=AD,∴FC=DE,(4分)
∴四边形CEDF是平行四边形.(5分)
(2)
解图
解:如解图,过点D作DH⊥BC于点H.
由(1)知四边形DECF是平行四边形,
∴DF=CE.(6分)
∵四边形ABCD是平行四边形,∠A=60°,AB=3,AD=4,
∴BC=4,CD=3,∠BCD=60°,(8分)
在Rt△DHC中,HC=DC·cos∠HCD=,
DH=DC·sin∠HCD=,
∵F是BC的中点,
∴FC=2,
∴FH=FC-HC=2-=,(10分)
在Rt△DFH中,由勾股定理得DF==
=,
∴CE=.(12分)
一、选择题
1. 如图,在平行四边形中,,,平分交边于点,则线段,的长度分别为( )
A.和 B.和 C.和 D.和如图
2. 如图,将?ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
3. 点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有( )种
A. B. C. D.
4. 如图,平行四边形ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( )
A. 3 cm B. 4 cm C. 5 cm D. 8 cm
5. 如图,在△ABC中,AB=4,BC=6,DE、DF是△ABC的中位线,则四边形BEDF的周长是( )
A. 5 B. 7 C. 8 D. 10
6. 如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
7. (2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
8. 已知四边形的四条边长分别是,其中为对边,并且满足
则这个四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.对角线垂直的四边形
二、填空题
9. (2020·牡丹江)如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件__________________,使四边形ABCD是平行四边形(填一个即可).
10. (2020·武汉)在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是□ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是____________.
11. 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.
12. (2020·凉山州)如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=1,△AOE的周长等于5,则平行四边形ABCD的周长等于 .
13. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
14. (2020·天津)如图,的顶点C在等边的边上,点E在的延长线上,G为的中点,连接.若,,则的长为_______.
15. 一个平行四边形的两条对角线的长分别为和,则它的一条边长的取值范围是 .
16. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
三、解答题
17. 在平行四边形中,过任作一直线,过、、作的垂线、、,垂足分别是、、,求证:.
18. 如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点M、N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求BN的长.
19. 已知:如图,平行四边形中,分别平分、、、,的延长线分别交于点.连接,若,.求的长.
20. 如图,将?ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
人教版 八年级下册数学 课时训练 18.1 平行四边形-答案
一、选择题
1. 【答案】B
2. 【答案】C 【解析】设∠ACD =x,∠B=y,则根据题意可列方程组,解得y=114°.
3. 【答案】B
4. 【答案】B 【解析】在?ABCD中,AD=BC,AB=CD,BO=DO,∵平行四边形ABCD的周长为26 cm,∴AB+BC=13 cm,又∵△AOD的周长比△AOB的周长多3 cm,∴AD-AB=BC-AB=3 cm,解得AB=5 cm,BC=8 cm,又AB⊥AC,E是BC的中点,∴AE=BE=CE=BC=4 cm.
5. 【答案】D 【解析】∵DE、DF是△ABC的中位线,∴DE∥AB,DF∥BC,DE=AB,DF=BC,∴四边形BEDF是平行四边形,∵AB=4,BC=6,∴DE=BF=2,DF=BE=3,∴四边形BEDF的周长为:2(DE+DF)=10.
6. 【答案】C
7. 【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
8. 【答案】B
二、填空题
9. 【答案】AD=BC
【解析】当添加条件AD=BC时,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD是平行四边形.
10. 【答案】26°
【解析】本题考查了等腰三角形性质,平行四边形性质等,∵□ABCD,∴AD=BC,AD∥BC,DC∥AB,又∵AD=AE=BE,∴BC=AE=BE,∴∠BAC=∠EBA,∠BEC=∠BCE,∵AD∥BC,DC∥AB,∴∠DCB=78°,∠BAC=∠DCA,∵∠BEC=∠BAC+∠EBA,∴∠BCE=2∠BAC,∴3∠BAC=78°,解得∠BAC=26°,因此本题答案为26°.
11. 【答案】110° 【解析】 ∵四边形ABCD是平行四边形,∴CD∥AB,∴∠CAB=∠1=20°,∵BE ⊥AB交对角线AC于点E,∴∠ABE=90°,∴∠2=∠CAB+∠ABE=20°+90°=110°.
12. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC.∵OE∥AB,∴OE是△ACD的中位线.∴AE=AD,OE=CD.∵OA=1,△AOE的周长等于5,∴AE+OE=4.∴AD+CD=8.∴平行四边形ABCD的周长=16.故答案为16.
13. 【答案】①;②
14. 【答案】
【解析】本题考查了平行四边形的性质、等边三角形的性质、中位线等知识点,延长DC交EF于点M,利用平行四边形、等边三角形性质求出相应的线段长,证出是的中位线是解题的关键.延长DC交EF于点M(图见详解),根据平行四边形与等边三角形的性质,可证△CFM是等边三角形,BF=BE=EF=BC+CF=5,可求出CF=CM=MF=2,可得C、G是DM和DE的中点,根据中位线的性质,可得出CG=,代入数值即可得出答案.如下图所示,延长DC交EF于点M,,,
平行四边形的顶点C在等边的边上,
,
是等边三角形,
.
在平行四边形中,,,
又是等边三角形,
,
.
G为的中点,,
是的中点,且是的中位线,
.
故答案为:.
15. 【答案】
【解析】如图,不妨设,,,在中,
,,由三角形三边关系可得
,即.
16. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
三、解答题
17. 【答案】
解法一:如图,过作于,则为矩形.
∴,.
又,∴.
又,∴.
∴,∴.
解法二:如图,延长到,使,连接,显然为矩形.
∴.
∵,,∴.
又∵,∴,∴.
∴.
18. 【答案】
(1)证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN,(1分)
又∵四边形ABCD是平行四边形,
∴MC∥AN,
∴四边形CMAN是平行四边形.(2分)
(2)解:∵四边形ABCD是平行四边形,
∴∠ADE=∠CBF,AD=CB,
又∵∠AED=∠CFB=90°,
∴△AED≌△CFB(AAS),(4分)
∴DE=BF=4,
∴在Rt△BFN中,BN==5.(5分)
19. 【答案】
∵四边形是平行四边形,∴,,,
∴,
∵平分,∴,∴,
∴.
∵平分,∴.
同理,,,
∴,∴,即,
∴四边形是平行四边形,∴,,
∴,,
∴四边形是平行四边形,
∴,∴.
20. 【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥FC.(2分)
∵F是BC的中点,
∴FC=BC=AD,
∵DE=AD,∴FC=DE,(4分)
∴四边形CEDF是平行四边形.(5分)
(2)
解图
解:如解图,过点D作DH⊥BC于点H.
由(1)知四边形DECF是平行四边形,
∴DF=CE.(6分)
∵四边形ABCD是平行四边形,∠A=60°,AB=3,AD=4,
∴BC=4,CD=3,∠BCD=60°,(8分)
在Rt△DHC中,HC=DC·cos∠HCD=,
DH=DC·sin∠HCD=,
∵F是BC的中点,
∴FC=2,
∴FH=FC-HC=2-=,(10分)
在Rt△DFH中,由勾股定理得DF==
=,
∴CE=.(12分)
