2020-2021学年人教版 数学八年级下册 课时训练 19.1 函数(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版 数学八年级下册 课时训练 19.1 函数(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 466.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:08:08 | ||
图片预览



文档简介
人教版 八年级下册数学 课时训练 19.1 函数
一、选择题
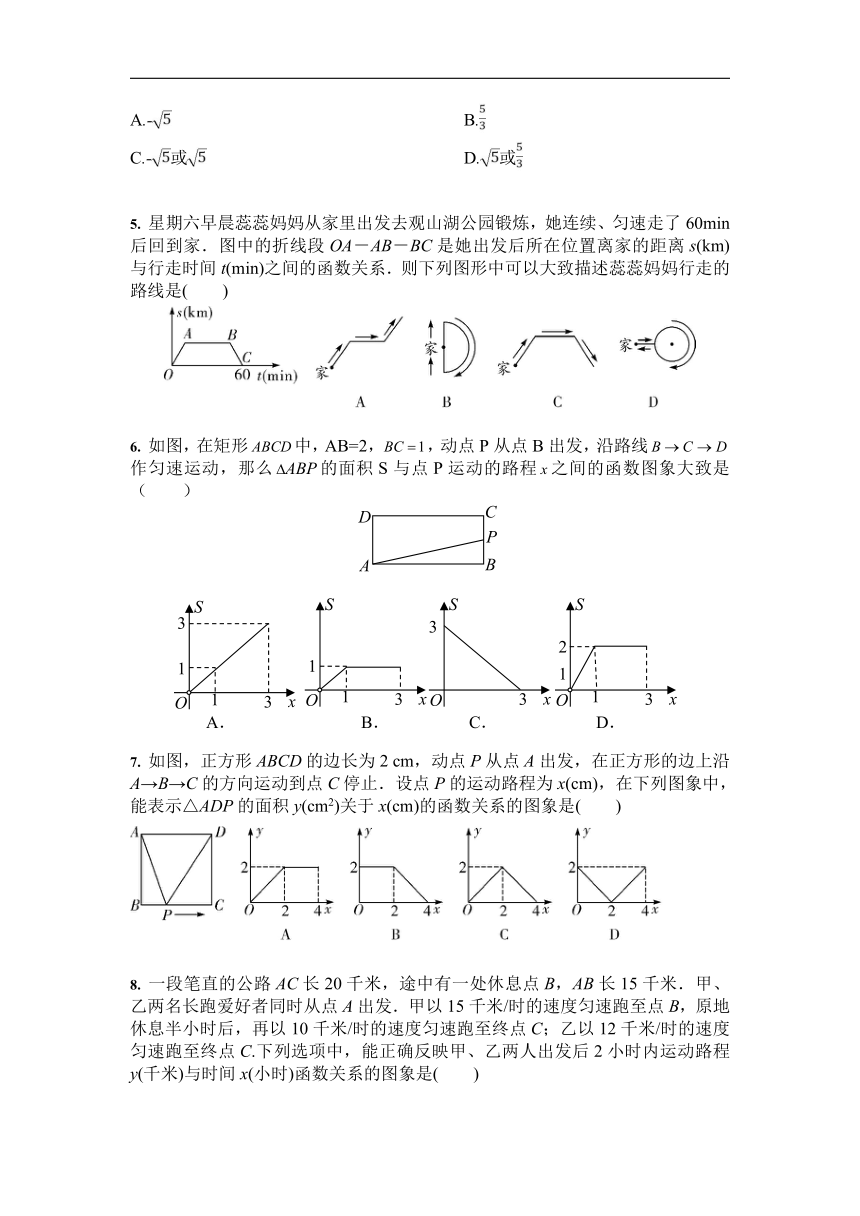
1. 图是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是 ( )
A.4 ℃ B.8 ℃ C.12 ℃ D.16 ℃
2. 小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图X3-1-4).若小亮上坡、平路、下坡的速度分别为v1、v2、v3,且v1
3. 同学在探究弹簧的长度与外力的变化关系时,试验记录得到相应数据如下表:
则y关于x的函数图象是 ( )
4. 已知函数y=当y=6时,x的值是 ( )
A.- B.
C.-或 D.或
5. 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回到家.图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系.则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
6. 如图,在矩形中,AB=2,,动点P从点B出发,沿路线作匀速运动,那么的面积S与点P运动的路程之间的函数图象大致是( )
7. 如图,正方形ABCD的边长为2 cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止.设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
8. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米.甲、乙两名长跑爱好者同时从点A出发.甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C.下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
二、填空题
9. 在函数y=中,自变量x的取值范围是________.
10. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一变量关系中, 是 的函数.?
11. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如下表所示的数据:
设鸭的质量为x千克,烤制时间为t分,估计当x=2.2时,t的值为 .?
12. (2019?湘潭)函数中,自变量的取值范围是__________.
13. 点(1,4) (填“在”或“不在”)函数y=-的图象上.?
14. 某油桶内有油20升,它有一个进油管和一个出油管,进油管每分钟进油4升,出油管每分钟出油6升.现同时打开两管,则油桶中剩余油量Q(升)与开管时间t(分)之间的函数关系式是 ,自变量t的取值范围是 .?
15. 某款手机的话费包含月租费和通话费,通话时间和费用之间的关系如下表:
在x,y这两个变量中,自变量是 ,y与x之间的函数关系式为 .
16. 弹簧挂上物体后会伸长,测得一弹簧长度y(cm)与所挂物体质量x(kg)在弹簧弹性范围内有如下表的关系,那么弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数关系式是 (不用体现自变量的取值范围).?
三、解答题
17. 已知函数y=+.
(1)求自变量x的取值范围;
(2)求当x=1时的函数值.
18. 用描点法画函数y=-的图象.
列表如下:
描点、连线:
根据图象回答下列问题.
(1)该图象与坐标轴有没有交点?为什么?
(2)在每个象限内,y随x的变化发生怎样的变化?
(3)判断点(3,-1)是否在该函数的图象上.
19. 如图,已知A(6,0),B(8,5),将线段OA平移至CB的位置,点D在x轴正半轴上(不与点A重合),连接OC,AB,AC,CD,BD.
(1)求AC的长.
(2)设点D的坐标为(x,0),△ODC与△ABD的面积分别记为S1,S2.设S=S1-S2,写出S关于x的函数解析式,并探究是否存在点D,使得S与△DBC的面积相等.如果存在,用坐标形式写出点D的位置;如果不存在,说明理由.
20. 刚回营地的两个抢险分队又接到救灾命令:一分队立即出发赶往30千米外的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再赶往A镇参加救灾.一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方处地形复杂,必须由一分队用1小时打通道路.已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.
(1)若二分队在营地不休息,问二分队几个小时能赶到A镇?
(2)若需要二分队和一分队同时赶到A镇,二分队应在营地休息几个小时?
(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理图象的代号,并说明它们的实际意义.
人教版 八年级下册数学 课时训练 19.1 函数-答案
一、选择题
1. 【答案】C
2. 【答案】C
3. 【答案】D [解析] 解题应抓住7.5 cm对应的x值以及x,y之间的关系.根据弹簧长度与外力的关系,在弹性限度内,砝码的质量每增加50 g,弹簧的长度伸长1 cm,则砝码的质量每增加1 g,弹簧的长度伸长 cm,所以y=x+2.因此当y=7.5时,x=275,观察图象知D正确.
4. 【答案】A
5. 【答案】B 【解析】由题图可知,OA段离家的距离s逐渐增大,AB段离家的距离s不变,BC段离家的距离s又逐渐减小,选项B中从圆心至圆弧上距离逐渐增大,在圆弧上距离圆心距离保持不变,圆弧另一端至圆心距离又逐渐减小,符合题图中离家距离的变化.
6. 【答案】B
【解析】了解点的运动路线,根据已知矩形的长和宽求出当点运动到点时的值为1,即当为1时的值为1,之后面积保持不变.
7. 【答案】A 【解析】当点P在AB上运动时,边AD恒定为2,高不断增大到2停止,则y随x的增大呈直线型由0增大到2,排除B、D;当点P在BC上运动时,△APD的边AD及AD边上的高均恒定不变,则随着x的增大,y值保持不变,排除C,故选A.
8. 【答案】A 【解析】由题意可知:甲所跑路程分为3个时段:开始1小时,以15千米/时的速度匀速由点A跑至点B,所跑路程为15千米;第1小时至第小时休息,所跑路程不变;第小时至第2小时,以10千米/时的速度匀速跑至终点C,所跑路程为5千米,即甲累计所跑路程为20千米时,所用时间为2小时,并且甲开始1小时内的速度大于第小时至第2小时之间的速度.因此选项A、C符合甲的情况.乙从点A出发,以12千米/时的速度匀速一直跑至终点C,所跑路程为20千米,所用时间为小时,并且乙的速度小于甲开始的速度但大于甲第3段的速度.所以选项A、B符合乙的情况.综上故选A.
二、填空题
9. 【答案】x≥-且x≠2 【解析】由题意得:x-2≠0且3x+1≥0,解得:x≥-且x≠2.
10. 【答案】骆驼的体温 时间
11. 【答案】108 [解析] 由表可知,质量每增加0.5千克,时间增加20分钟,则质量每增加1千克,时间增加40分钟.质量为2千克时,时间为100分钟,所以2.2千克时,时间为108分钟,故t的值为108.
12. 【答案】
【解析】由题意得,,
解得
故答案为:.
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
13. 【答案】不在
14. 【答案】Q=20-2t 0≤t≤10
15. 【答案】x y=0.3x+15
16. 【答案】y=0.5x+12
三、解答题
17. 【答案】
解:(1)根据题意,得解得x<5.
故x的取值范围为x<5.
(2)把x=1代入解析式,得
y=+=2-1=1.
18. 【答案】
解:表格从左到右依次填:1,2,4,6,-6,-4,-2,-1.描点、连线略.
(1)该图象与坐标轴没有交点,因为自变量x的值不可能为0,函数值y也不可能为0.
(2)在每个象限内,y随x值的增大而增大.
(3)当x=3时,y=-,所以点(3,-1)不在该函数的图象上.
19. 【答案】
解:(1)因为将线段OA平移至CB的位置,
所以OA∥CB,OA=CB,
所以四边形OABC为平行四边形.
又知A(6,0),B(8,5),所以C(2,5).
过点C作CE⊥OA于点E,则OE=2,EA=4,CE=5.
在Rt△CEA中,AC===.
(2)当0S1=x,S2=(6-x),
所以S=S1-S2=5x-15.
当x>6,即当点D在线段OA的延长线上时,
S1=x,S2=(x-6),
所以S=S1-S2=15.
综上所述,S=
存在点D使得S与 △DBC的面积相等.
当0所以当S=S△DBC时,5x-15=15,解得x=6(与点A重合,不合题意,舍去).
当x>6时,S=15=S△DBC,所以点D的位置为(x,0)且x>6.
20. 【答案】
解:(1)若二分队在营地不休息,则a=0,速度为4千米/时,行至塌方处需=2.5(小时),因为一分队到塌方处并打通道路需要+1=3(小时),故二分队在塌方处需要停留0.5小时,所以二分队在营地不休息赶到A镇需2.5+0.5+=8(小时).
(2)一分队赶到A镇共需+1=7(小时).
(ⅰ)若二分队在塌方处需停留,则后20千米需与一分队同行,故4+a=5,即a=1,这与二分队在塌方处停留矛盾,舍去;
(ⅱ)若二分队在塌方处不停留,则(4+a)(7-a)=30,即a2-3a+2=0,解得a1=1,a2=2.
经检验a1=1,a2=2均符合题意.
答:二分队应在营地休息1小时或2小时.(其他解法只要合理即给分)
(3)合理的图象为(b)、(d).
图象(b)表明二分队在营地休息时间恰当(2<a≤3),后于一分队赶到A镇;
图象(d)表明二分队在营地休息时间恰当(1<a<2),先于一分队赶到A镇.
一、选择题
1. 图是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是 ( )
A.4 ℃ B.8 ℃ C.12 ℃ D.16 ℃
2. 小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图X3-1-4).若小亮上坡、平路、下坡的速度分别为v1、v2、v3,且v1
3. 同学在探究弹簧的长度与外力的变化关系时,试验记录得到相应数据如下表:
则y关于x的函数图象是 ( )
4. 已知函数y=当y=6时,x的值是 ( )
A.- B.
C.-或 D.或
5. 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回到家.图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系.则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
6. 如图,在矩形中,AB=2,,动点P从点B出发,沿路线作匀速运动,那么的面积S与点P运动的路程之间的函数图象大致是( )
7. 如图,正方形ABCD的边长为2 cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止.设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
8. 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米.甲、乙两名长跑爱好者同时从点A出发.甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C.下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是( )
二、填空题
9. 在函数y=中,自变量x的取值范围是________.
10. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一变量关系中, 是 的函数.?
11. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如下表所示的数据:
设鸭的质量为x千克,烤制时间为t分,估计当x=2.2时,t的值为 .?
12. (2019?湘潭)函数中,自变量的取值范围是__________.
13. 点(1,4) (填“在”或“不在”)函数y=-的图象上.?
14. 某油桶内有油20升,它有一个进油管和一个出油管,进油管每分钟进油4升,出油管每分钟出油6升.现同时打开两管,则油桶中剩余油量Q(升)与开管时间t(分)之间的函数关系式是 ,自变量t的取值范围是 .?
15. 某款手机的话费包含月租费和通话费,通话时间和费用之间的关系如下表:
在x,y这两个变量中,自变量是 ,y与x之间的函数关系式为 .
16. 弹簧挂上物体后会伸长,测得一弹簧长度y(cm)与所挂物体质量x(kg)在弹簧弹性范围内有如下表的关系,那么弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数关系式是 (不用体现自变量的取值范围).?
三、解答题
17. 已知函数y=+.
(1)求自变量x的取值范围;
(2)求当x=1时的函数值.
18. 用描点法画函数y=-的图象.
列表如下:
描点、连线:
根据图象回答下列问题.
(1)该图象与坐标轴有没有交点?为什么?
(2)在每个象限内,y随x的变化发生怎样的变化?
(3)判断点(3,-1)是否在该函数的图象上.
19. 如图,已知A(6,0),B(8,5),将线段OA平移至CB的位置,点D在x轴正半轴上(不与点A重合),连接OC,AB,AC,CD,BD.
(1)求AC的长.
(2)设点D的坐标为(x,0),△ODC与△ABD的面积分别记为S1,S2.设S=S1-S2,写出S关于x的函数解析式,并探究是否存在点D,使得S与△DBC的面积相等.如果存在,用坐标形式写出点D的位置;如果不存在,说明理由.
20. 刚回营地的两个抢险分队又接到救灾命令:一分队立即出发赶往30千米外的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再赶往A镇参加救灾.一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方处地形复杂,必须由一分队用1小时打通道路.已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.
(1)若二分队在营地不休息,问二分队几个小时能赶到A镇?
(2)若需要二分队和一分队同时赶到A镇,二分队应在营地休息几个小时?
(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理图象的代号,并说明它们的实际意义.
人教版 八年级下册数学 课时训练 19.1 函数-答案
一、选择题
1. 【答案】C
2. 【答案】C
3. 【答案】D [解析] 解题应抓住7.5 cm对应的x值以及x,y之间的关系.根据弹簧长度与外力的关系,在弹性限度内,砝码的质量每增加50 g,弹簧的长度伸长1 cm,则砝码的质量每增加1 g,弹簧的长度伸长 cm,所以y=x+2.因此当y=7.5时,x=275,观察图象知D正确.
4. 【答案】A
5. 【答案】B 【解析】由题图可知,OA段离家的距离s逐渐增大,AB段离家的距离s不变,BC段离家的距离s又逐渐减小,选项B中从圆心至圆弧上距离逐渐增大,在圆弧上距离圆心距离保持不变,圆弧另一端至圆心距离又逐渐减小,符合题图中离家距离的变化.
6. 【答案】B
【解析】了解点的运动路线,根据已知矩形的长和宽求出当点运动到点时的值为1,即当为1时的值为1,之后面积保持不变.
7. 【答案】A 【解析】当点P在AB上运动时,边AD恒定为2,高不断增大到2停止,则y随x的增大呈直线型由0增大到2,排除B、D;当点P在BC上运动时,△APD的边AD及AD边上的高均恒定不变,则随着x的增大,y值保持不变,排除C,故选A.
8. 【答案】A 【解析】由题意可知:甲所跑路程分为3个时段:开始1小时,以15千米/时的速度匀速由点A跑至点B,所跑路程为15千米;第1小时至第小时休息,所跑路程不变;第小时至第2小时,以10千米/时的速度匀速跑至终点C,所跑路程为5千米,即甲累计所跑路程为20千米时,所用时间为2小时,并且甲开始1小时内的速度大于第小时至第2小时之间的速度.因此选项A、C符合甲的情况.乙从点A出发,以12千米/时的速度匀速一直跑至终点C,所跑路程为20千米,所用时间为小时,并且乙的速度小于甲开始的速度但大于甲第3段的速度.所以选项A、B符合乙的情况.综上故选A.
二、填空题
9. 【答案】x≥-且x≠2 【解析】由题意得:x-2≠0且3x+1≥0,解得:x≥-且x≠2.
10. 【答案】骆驼的体温 时间
11. 【答案】108 [解析] 由表可知,质量每增加0.5千克,时间增加20分钟,则质量每增加1千克,时间增加40分钟.质量为2千克时,时间为100分钟,所以2.2千克时,时间为108分钟,故t的值为108.
12. 【答案】
【解析】由题意得,,
解得
故答案为:.
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
13. 【答案】不在
14. 【答案】Q=20-2t 0≤t≤10
15. 【答案】x y=0.3x+15
16. 【答案】y=0.5x+12
三、解答题
17. 【答案】
解:(1)根据题意,得解得x<5.
故x的取值范围为x<5.
(2)把x=1代入解析式,得
y=+=2-1=1.
18. 【答案】
解:表格从左到右依次填:1,2,4,6,-6,-4,-2,-1.描点、连线略.
(1)该图象与坐标轴没有交点,因为自变量x的值不可能为0,函数值y也不可能为0.
(2)在每个象限内,y随x值的增大而增大.
(3)当x=3时,y=-,所以点(3,-1)不在该函数的图象上.
19. 【答案】
解:(1)因为将线段OA平移至CB的位置,
所以OA∥CB,OA=CB,
所以四边形OABC为平行四边形.
又知A(6,0),B(8,5),所以C(2,5).
过点C作CE⊥OA于点E,则OE=2,EA=4,CE=5.
在Rt△CEA中,AC===.
(2)当0
所以S=S1-S2=5x-15.
当x>6,即当点D在线段OA的延长线上时,
S1=x,S2=(x-6),
所以S=S1-S2=15.
综上所述,S=
存在点D使得S与 △DBC的面积相等.
当0
当x>6时,S=15=S△DBC,所以点D的位置为(x,0)且x>6.
20. 【答案】
解:(1)若二分队在营地不休息,则a=0,速度为4千米/时,行至塌方处需=2.5(小时),因为一分队到塌方处并打通道路需要+1=3(小时),故二分队在塌方处需要停留0.5小时,所以二分队在营地不休息赶到A镇需2.5+0.5+=8(小时).
(2)一分队赶到A镇共需+1=7(小时).
(ⅰ)若二分队在塌方处需停留,则后20千米需与一分队同行,故4+a=5,即a=1,这与二分队在塌方处停留矛盾,舍去;
(ⅱ)若二分队在塌方处不停留,则(4+a)(7-a)=30,即a2-3a+2=0,解得a1=1,a2=2.
经检验a1=1,a2=2均符合题意.
答:二分队应在营地休息1小时或2小时.(其他解法只要合理即给分)
(3)合理的图象为(b)、(d).
图象(b)表明二分队在营地休息时间恰当(2<a≤3),后于一分队赶到A镇;
图象(d)表明二分队在营地休息时间恰当(1<a<2),先于一分队赶到A镇.
