2020-2021学年北师大版八年级下册数学 1.2直角三角形 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年北师大版八年级下册数学 1.2直角三角形 同步练习(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览




文档简介
1.2直角三角形 同步练习
一.选择题
1.在△ABC中,∠C=90°,∠A=60°,AC=2.则AB的长为( )
A.1 B.2 C.3 D.4
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2 B.4 C.6 D.8
3.如图,在△ABC中,∠ACB=90°,过点C作CD∥AB交∠ABC的平分线于点D,若∠ABD=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.50°
4.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=( )
A.6cm B.5cm C.4cm D.3cm
5.如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )
A.3 B.3.5 C.4 D.4.5
6.如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若NM=4,则OM的值( )
A.2 B.3 C.4 D.5
7.如图所示,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥BC,E为垂足,AC=AB,图中为60°的角有( )
A.2个 B.3个 C.4个 D.5个
8.直角三角形的两条直角边为3,4,则这个直角三角形斜边上的中线长为( )
A.5 B.2.5 C.3.5 D.4.5
9.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是( )
A.2﹣x B.3﹣x C.1 D.2+x
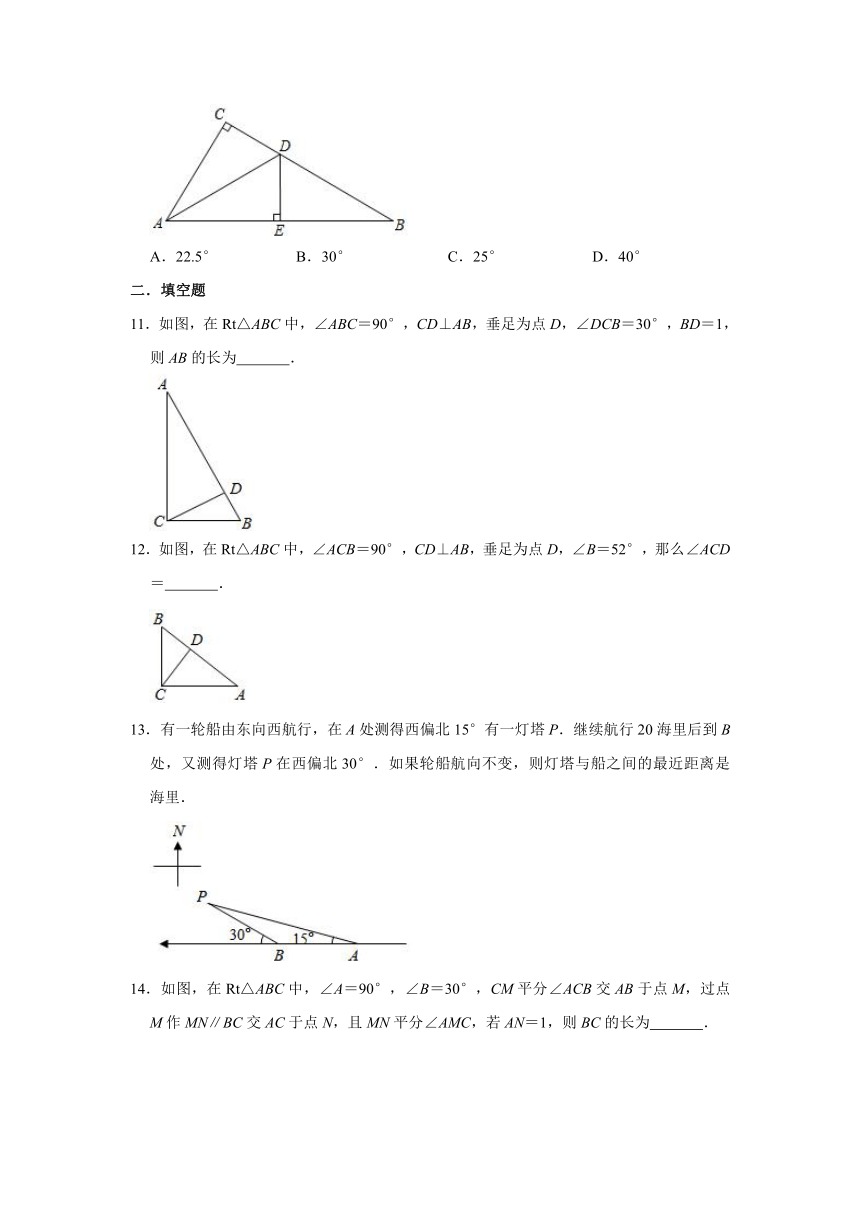
10.如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB于点E,DE平分∠ADB,则∠DBA等于( )
A.22.5° B.30° C.25° D.40°
二.填空题
11.如图,在Rt△ABC中,∠ABC=90°,CD⊥AB,垂足为点D,∠DCB=30°,BD=1,则AB的长为 .
12.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,∠B=52°,那么∠ACD= .
13.有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,则灯塔与船之间的最近距离是 海里.
14.如图,在Rt△ABC中,∠A=90°,∠B=30°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为 .
15.如图,在Rt△ABC中,∠ACB=90°,点D、E分别在边BC、AB上,CD=BD,CE=AB,AD与CE交于点F,如果AB=6,那么CF的长等于 .
三.解答题
16.如图,在△ABC中,D是BC的中点,AD=BC.求证:∠BAC=90°.
17.如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AM平分∠BAC,AM的长为15cm,求BC的长.
18.如图,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明你的猜想.
(3)当∠BAC变为钝角时,如图②,上述(1)(2)中的结论是否都成立?若成立,直接回答,不需证明;若不成立,请说明理由.
参考答案
一.选择题
1.解:∵∠C=90°,∠A=60°,
∴∠B=90°﹣∠A=30°,
∵AC=2,
∴AB=2AC=4.
故选:D.
2.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=60°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=AB﹣AD=8﹣2=6.
故选:C.
3.解:∵BD平分∠ABC,
∴∠ABD=∠DBC=20°,
∴∠ABC=40°,
∵∠ACB=90°,
∴∠A=90°﹣∠ABC=90°﹣40°=50°,
∵CD∥AB,
∴∠ACD=∠A=50°,
故选:D.
4.解:∵DE垂直平分AB,
∴EB=EA,
∴∠EAB=∠B=15°,
∴∠AEC=30°,
∴AC=AE=3(cm),
故选:D.
5.解:过点P作PD⊥CB于点D,
∵∠ACB=60°,PD⊥CB,PC=12,
∴DC=6,
∵PM=PN,MN=3,PD⊥OB,
∴MD=ND=1.5,
∴CM=6﹣1.5=4.5.
故选:D.
6.解:过点P作PH⊥MN于H,
∵PM=PN,
∴MH=NH=MN=2,
∵∠AOB=60°,
∴∠OPH=30°,
∵OP=10,
∴OH=OP=5,
∴OM=OH﹣MH=3,
故选:B.
7.解:在Rt△ABC中,∠ACB=90°,AC=AB,
∴∠B=30°.
∵D是AB的中点,
∴BD=CD.
∴∠DCB=∠B=30°.
又∵DE⊥BC于E,
∴∠BDE=∠CDE=60°.
∴∠ACD=90°﹣30°=60°.
∴△ACD为等边三角形.
∴∠ADC=∠DAC=∠ACD=∠CDE=∠BDE=60°.
故选:D.
8.解:由勾股定理得:直角三角形的斜边长是=5,
所以=2.5,
故选:B.
9.解:∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°,
∵PD⊥BC,DE⊥AC,
∴BD=PB,CE=CD,
∵PA=x,
∴BP=4﹣x,
∴BD=PB=2﹣x,
∴CD=4﹣(2﹣x)=2+x,
∴CE=1+x,
∴AE=4﹣(1+x)=3﹣x,
故选:B.
10.解:在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,
∴CD=ED.
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE.
∵∠ADC+∠ADE+∠EDB=180°,DE平分∠ADB,
∴∠ADC=∠ADE=∠EDB=60°.
∴∠B+∠EDB=90°,
∴∠B=30°.
故选:B.
二.填空题
11.解:在Rt△ABC中,∠ABC=90°,∠DCB=30°,
∴2BD=BC,
∵CD⊥AB,
∴∠A=∠DCB=30°,
∴2BC=AB,
∴AB=4BD,
∵BD=1,
∴AB=4.
故答案为:4.
12.解:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵∠B=52°,
∴∠ACD=52°,
故答案为:52°.
13.解:如图:过P作PD⊥AB于D,则PD的长就是灯塔与船之间的最近距离,
∴∠PDB=90°,
∵∠PBD=30°,∠PAB=15°,
∴∠APB=∠PBD﹣∠PAB=15°=∠PAB,
∴PB=AB=20(海里),
在Rt△PBD中,PB=20海里,∠PBD=30°,
∴PD=PB=10(海里),
故答案为:10.
14.解:在Rt△ABC中,∠A=90°,∠B=30°,
∴∠ACB=60°,
∵MN∥BC,
∴∠AMN=∠B=30°,
∵∠A=90°,AN=1,
∴MN=2AN=2,
∵MN平分∠AMC,∠AMN=30°,
∴∠AMC=∠NMC=60°,
∵CM平分∠ACB,∠ACB=60°,
∴∠ACM=ACB=30°,
∴∠ACM=∠NMC,
∴MNCN=2,
∴AC=AN+CN=1+2=3,
∵在Rt△ABC中,∠A=90°,∠B=30°,
∴BC=2AC=2×3=6,
故答案为:6.
15.解:以E为圆心,CE为半径画圆,
∵∠ACB=90°,
∴AB是⊙E的直径,
∵CE=AB,
∴点E是AB的中点,
连接DE,
在Rt△ABC中,∠ACB=90°,CE=AB,
∴AE=BE,∵CD=BD,
∴DE是Rt△ABC的中位线,
∴DE=AC,DE∥AC,
∴△ACF∽△DEF,
∴==,
∵AB=6,
∴CE=AB=3,
∴CF=CE=2,
故答案为:2.
三.解答题
16.证明:在△ABC中,D是BC的中点,AD=BC,
∴AD=DC,AD=DB,
∴∠C=∠DAC,∠B=∠BAD,
∴∠BAC=∠BAD+∠DAC=∠B+∠C,
由三角形的内角和定理可得:
∠BAC+(∠B+∠C)=2∠BAC=180°,
∴∠BAC=90°.
17.解:∵AM是∠BAC的平分线,∠BAC=60°,
∴∠MAC=30°,
∴MC=AM=7.5cm,
∴AC=(cm),
∵在△ABC中,∠C=90°,∠BAC=60°,
∴∠ABC=30°,
∴AB=2AC=15(cm),
∴BC=(cm).
18.(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=BC,ME=BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)
=360°﹣2(∠ABC+∠ACB)
=360°﹣2(180°﹣∠A)
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连结DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC
=2(180°﹣∠BAC)
=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC)
=2∠BAC﹣180°.
一.选择题
1.在△ABC中,∠C=90°,∠A=60°,AC=2.则AB的长为( )
A.1 B.2 C.3 D.4
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2 B.4 C.6 D.8
3.如图,在△ABC中,∠ACB=90°,过点C作CD∥AB交∠ABC的平分线于点D,若∠ABD=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.50°
4.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=( )
A.6cm B.5cm C.4cm D.3cm
5.如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )
A.3 B.3.5 C.4 D.4.5
6.如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若NM=4,则OM的值( )
A.2 B.3 C.4 D.5
7.如图所示,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥BC,E为垂足,AC=AB,图中为60°的角有( )
A.2个 B.3个 C.4个 D.5个
8.直角三角形的两条直角边为3,4,则这个直角三角形斜边上的中线长为( )
A.5 B.2.5 C.3.5 D.4.5
9.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是( )
A.2﹣x B.3﹣x C.1 D.2+x
10.如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB于点E,DE平分∠ADB,则∠DBA等于( )
A.22.5° B.30° C.25° D.40°
二.填空题
11.如图,在Rt△ABC中,∠ABC=90°,CD⊥AB,垂足为点D,∠DCB=30°,BD=1,则AB的长为 .
12.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,∠B=52°,那么∠ACD= .
13.有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,则灯塔与船之间的最近距离是 海里.
14.如图,在Rt△ABC中,∠A=90°,∠B=30°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为 .
15.如图,在Rt△ABC中,∠ACB=90°,点D、E分别在边BC、AB上,CD=BD,CE=AB,AD与CE交于点F,如果AB=6,那么CF的长等于 .
三.解答题
16.如图,在△ABC中,D是BC的中点,AD=BC.求证:∠BAC=90°.
17.如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AM平分∠BAC,AM的长为15cm,求BC的长.
18.如图,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明你的猜想.
(3)当∠BAC变为钝角时,如图②,上述(1)(2)中的结论是否都成立?若成立,直接回答,不需证明;若不成立,请说明理由.
参考答案
一.选择题
1.解:∵∠C=90°,∠A=60°,
∴∠B=90°﹣∠A=30°,
∵AC=2,
∴AB=2AC=4.
故选:D.
2.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=60°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=AB﹣AD=8﹣2=6.
故选:C.
3.解:∵BD平分∠ABC,
∴∠ABD=∠DBC=20°,
∴∠ABC=40°,
∵∠ACB=90°,
∴∠A=90°﹣∠ABC=90°﹣40°=50°,
∵CD∥AB,
∴∠ACD=∠A=50°,
故选:D.
4.解:∵DE垂直平分AB,
∴EB=EA,
∴∠EAB=∠B=15°,
∴∠AEC=30°,
∴AC=AE=3(cm),
故选:D.
5.解:过点P作PD⊥CB于点D,
∵∠ACB=60°,PD⊥CB,PC=12,
∴DC=6,
∵PM=PN,MN=3,PD⊥OB,
∴MD=ND=1.5,
∴CM=6﹣1.5=4.5.
故选:D.
6.解:过点P作PH⊥MN于H,
∵PM=PN,
∴MH=NH=MN=2,
∵∠AOB=60°,
∴∠OPH=30°,
∵OP=10,
∴OH=OP=5,
∴OM=OH﹣MH=3,
故选:B.
7.解:在Rt△ABC中,∠ACB=90°,AC=AB,
∴∠B=30°.
∵D是AB的中点,
∴BD=CD.
∴∠DCB=∠B=30°.
又∵DE⊥BC于E,
∴∠BDE=∠CDE=60°.
∴∠ACD=90°﹣30°=60°.
∴△ACD为等边三角形.
∴∠ADC=∠DAC=∠ACD=∠CDE=∠BDE=60°.
故选:D.
8.解:由勾股定理得:直角三角形的斜边长是=5,
所以=2.5,
故选:B.
9.解:∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°,
∵PD⊥BC,DE⊥AC,
∴BD=PB,CE=CD,
∵PA=x,
∴BP=4﹣x,
∴BD=PB=2﹣x,
∴CD=4﹣(2﹣x)=2+x,
∴CE=1+x,
∴AE=4﹣(1+x)=3﹣x,
故选:B.
10.解:在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,
∴CD=ED.
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE.
∵∠ADC+∠ADE+∠EDB=180°,DE平分∠ADB,
∴∠ADC=∠ADE=∠EDB=60°.
∴∠B+∠EDB=90°,
∴∠B=30°.
故选:B.
二.填空题
11.解:在Rt△ABC中,∠ABC=90°,∠DCB=30°,
∴2BD=BC,
∵CD⊥AB,
∴∠A=∠DCB=30°,
∴2BC=AB,
∴AB=4BD,
∵BD=1,
∴AB=4.
故答案为:4.
12.解:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵∠B=52°,
∴∠ACD=52°,
故答案为:52°.
13.解:如图:过P作PD⊥AB于D,则PD的长就是灯塔与船之间的最近距离,
∴∠PDB=90°,
∵∠PBD=30°,∠PAB=15°,
∴∠APB=∠PBD﹣∠PAB=15°=∠PAB,
∴PB=AB=20(海里),
在Rt△PBD中,PB=20海里,∠PBD=30°,
∴PD=PB=10(海里),
故答案为:10.
14.解:在Rt△ABC中,∠A=90°,∠B=30°,
∴∠ACB=60°,
∵MN∥BC,
∴∠AMN=∠B=30°,
∵∠A=90°,AN=1,
∴MN=2AN=2,
∵MN平分∠AMC,∠AMN=30°,
∴∠AMC=∠NMC=60°,
∵CM平分∠ACB,∠ACB=60°,
∴∠ACM=ACB=30°,
∴∠ACM=∠NMC,
∴MNCN=2,
∴AC=AN+CN=1+2=3,
∵在Rt△ABC中,∠A=90°,∠B=30°,
∴BC=2AC=2×3=6,
故答案为:6.
15.解:以E为圆心,CE为半径画圆,
∵∠ACB=90°,
∴AB是⊙E的直径,
∵CE=AB,
∴点E是AB的中点,
连接DE,
在Rt△ABC中,∠ACB=90°,CE=AB,
∴AE=BE,∵CD=BD,
∴DE是Rt△ABC的中位线,
∴DE=AC,DE∥AC,
∴△ACF∽△DEF,
∴==,
∵AB=6,
∴CE=AB=3,
∴CF=CE=2,
故答案为:2.
三.解答题
16.证明:在△ABC中,D是BC的中点,AD=BC,
∴AD=DC,AD=DB,
∴∠C=∠DAC,∠B=∠BAD,
∴∠BAC=∠BAD+∠DAC=∠B+∠C,
由三角形的内角和定理可得:
∠BAC+(∠B+∠C)=2∠BAC=180°,
∴∠BAC=90°.
17.解:∵AM是∠BAC的平分线,∠BAC=60°,
∴∠MAC=30°,
∴MC=AM=7.5cm,
∴AC=(cm),
∵在△ABC中,∠C=90°,∠BAC=60°,
∴∠ABC=30°,
∴AB=2AC=15(cm),
∴BC=(cm).
18.(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=BC,ME=BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)
=360°﹣2(∠ABC+∠ACB)
=360°﹣2(180°﹣∠A)
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连结DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC
=2(180°﹣∠BAC)
=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC)
=2∠BAC﹣180°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
