沪科版八年级数学下册:18.1 勾股定理 同步练习(word版,含答案)
文档属性
| 名称 | 沪科版八年级数学下册:18.1 勾股定理 同步练习(word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览



文档简介
18.1 勾股定理
一.选择题
1.如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
A.小正方形面积为4 B.x2+y2=5
C.x2﹣y2=7 D.xy=24
2.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE
D.S四边形AECD=S四边形DEBC
3.如图,四个全等的直角三角形围成正方形ABCD和正方形EFGH,即赵爽弦图.连接AC,分别交EF、GH于点M,N,连接FN.已知AH=3DH,且S正方形ABCD=21,则图中阴影部分的面积之和为( )
A. B. C. D.
4.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A.50 B.16 C.25 D.41
5.如图所示的是一种“羊头”形图案,全部由正方形与等腰直角三角形构成,其作法是从正方形①开始,以它的一条边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,再分别以正方形②和②的一条边为斜边,向外作等腰直角三角形,…,若正方形⑤的面积为2cm2,则正方形①的面积为( )
A.8cm2 B.16cm2 C.32cm2 D.64ccm2
6.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的值不可能为( )
A.5 B.8 C. D.
7.如图所示,在△ABC中,∠ABC=90°,分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
A.175 B.600 C.25 D.625
8.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上,AD=AC,AE⊥CD,垂足为F,与BC交于点E,则BE的长是( )
A.3 B.5 C. D.6
9.如图是一株美丽的勾股树,其中所有四边形都是正方形,所有的三角形都是直角三角形若正方形A、B、C、D的面积分别为3、5、2、3,则最大正方形E的面积是( )
A.47 B.13 C.11 D.8
10.若直角三角形中,斜边的长为17,一条直角边长为15,则另一条直角边长为( )
A.7 B.8 C.20 D.65
11.如图,在△ABC中,∠C=90°,AB=12,AC=6,则BC等于( )
A.6 B.6 C.6 D.12
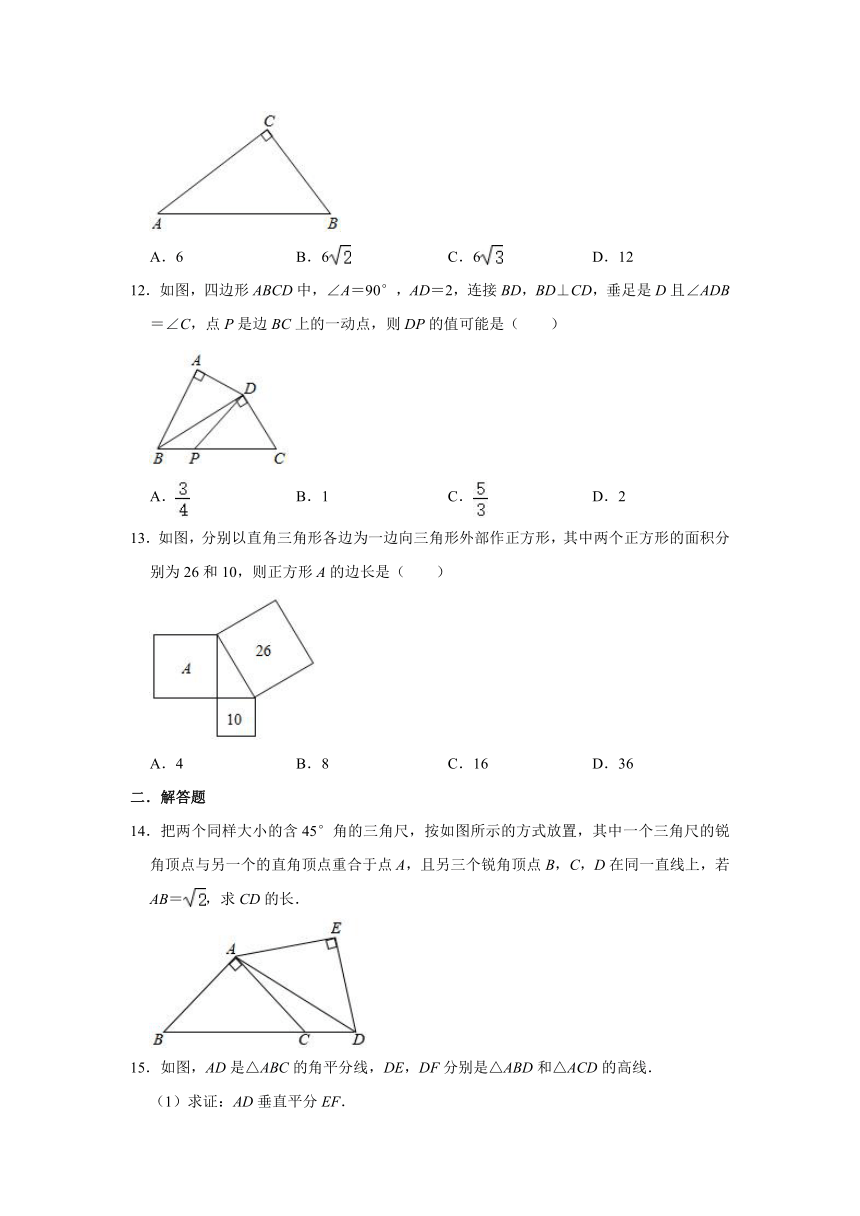
12.如图,四边形ABCD中,∠A=90°,AD=2,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的值可能是( )
A. B.1 C. D.2
13.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为26和10,则正方形A的边长是( )
A.4 B.8 C.16 D.36
二.解答题
14.把两个同样大小的含45°角的三角尺,按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上,若AB=,求CD的长.
15.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高线.
(1)求证:AD垂直平分EF.
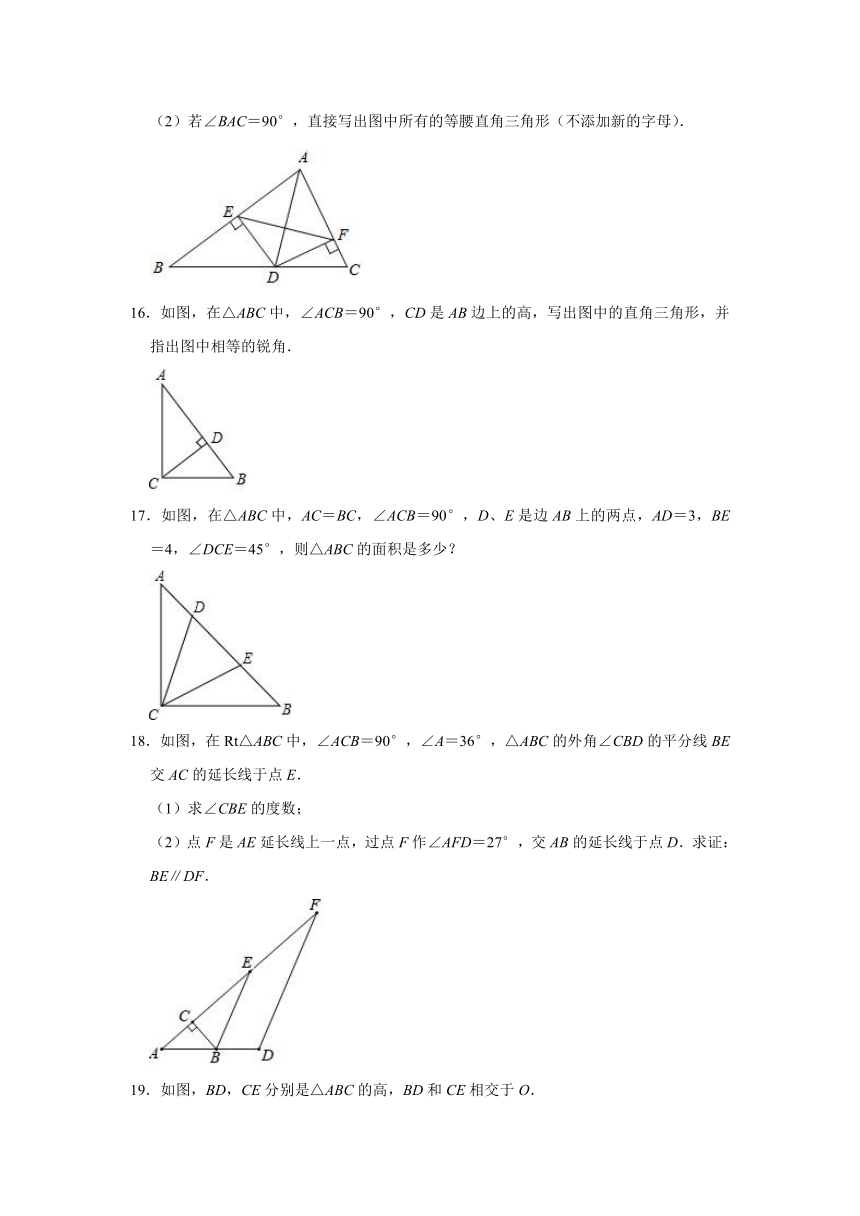
(2)若∠BAC=90°,直接写出图中所有的等腰直角三角形(不添加新的字母).
16.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,写出图中的直角三角形,并指出图中相等的锐角.
17.如图,在△ABC中,AC=BC,∠ACB=90°,D、E是边AB上的两点,AD=3,BE=4,∠DCE=45°,则△ABC的面积是多少?
18.如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
19.如图,BD,CE分别是△ABC的高,BD和CE相交于O.
(1)图中有哪几个直角三角形?
(2)图中有与∠2相等的角吗?请说明理由;
(3)若∠A=55°,∠ACB=65°,求∠3,∠4和∠5的度数.
参考答案
一.选择题
1. C.
2. B.
3. B.
4. A.
5. C.
6. C.
7. D.
8. B.
9. B.
10. B.
11. A.
12. D.
13. A.
二.解答题
14.解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BC=AB=2,BF=AF=AB=1,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=2,
在Rt△ADF中,根据勾股定理得,DF==,
∴CD=BF+DF﹣BC=1+﹣2=﹣1.
15.解:(1)∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,
在Rt△AED和Rt△AFD中,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,又DE=DF,
∴AD垂直平分EF;
(2)∵∠BAC=90°,AE=AF,
∴△AEF是等腰直角三角形,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠EAF=∠AFD=90°,
∴四边形AEDF是正方形,
∴∠EDF=90°,
∴△EDF是等腰直角三角形.
16.解:∵∠ACB=90°,
∴△ABC为直角三角形,
∵CD⊥AB,
∴△ADC、△BDC为直角三角形,
∴图中直角三角形有△ABC、△ADC、△BDC,
∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠CDB=∠ADB=90°,
∴∠BCD+∠B=90°,∠ACD+∠A=90°,
∴∠BCD=∠A,∠B=∠ACD.
17.解:∵AC=BC,∠ACB=90°,
∴∠ABC=∠CAB=45°,
设DE=x,则AB=AD+BE+DE=3+4+x=7+x,
∵∠DCE=∠CAE=∠DBC=45°,∠AEC=∠CED,∠BDC=∠CDE,
∴△ACE∽△CDE∽△BDC,
设CD=a,CE=b,
则有以下等式:
x:b=b:3+x,x:a=a:4+x,x:a=b:AC,
整理得,b2=x(x+3),a2=x(x+4),x?AC=ab,
则x2(x+3)(x+4)=a2b2=x2?AC2=,
解得,x=5;
∴AB=12,
∴AC=BC=6,
∴S△ABC=AC×BC=×6×6=36,
答:△ABC的面积是36.
18.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°﹣∠A=54°,
∴∠CBD=126°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=63°;
(2)∵∠ACB=90°,∠CBE=63°,
∴∠CEB=90°﹣63°=27°.
又∵∠F=27°,
∴∠F=∠CEB=27°,
∴DF∥BE
19.解:(1)∵BD,CE分别是△ABC的高,
∴∠ADB=∠CDB=∠AEC=∠BEC=90°,
∴图中有6个直角三角形,分别为△ABD、△CBD、△ACE、△BCE、△OBE、△OCD;
(2)图中有与∠2相等的角为∠1,理由如下:
∵∠2+∠A=90°,∠1+∠A=90°,
∴∠1=∠2;
(3)∵∠CDB=90°,∠ACB=65°,
∴∠3=90°﹣∠ACB=90°﹣65°=25°,
∵∠A=55°,∠ACB=65°,
∴∠ABC=180°﹣∠A﹣∠ACB=180°﹣55°﹣65°=60°,
∵∠BEC=90°,
∴∠4=90°﹣∠ABC=30°,
∴∠5=∠BOC=180°﹣∠3﹣∠4=180°﹣25°﹣30°=125°.
一.选择题
1.如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
A.小正方形面积为4 B.x2+y2=5
C.x2﹣y2=7 D.xy=24
2.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE
D.S四边形AECD=S四边形DEBC
3.如图,四个全等的直角三角形围成正方形ABCD和正方形EFGH,即赵爽弦图.连接AC,分别交EF、GH于点M,N,连接FN.已知AH=3DH,且S正方形ABCD=21,则图中阴影部分的面积之和为( )
A. B. C. D.
4.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A.50 B.16 C.25 D.41
5.如图所示的是一种“羊头”形图案,全部由正方形与等腰直角三角形构成,其作法是从正方形①开始,以它的一条边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,再分别以正方形②和②的一条边为斜边,向外作等腰直角三角形,…,若正方形⑤的面积为2cm2,则正方形①的面积为( )
A.8cm2 B.16cm2 C.32cm2 D.64ccm2
6.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的值不可能为( )
A.5 B.8 C. D.
7.如图所示,在△ABC中,∠ABC=90°,分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
A.175 B.600 C.25 D.625
8.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上,AD=AC,AE⊥CD,垂足为F,与BC交于点E,则BE的长是( )
A.3 B.5 C. D.6
9.如图是一株美丽的勾股树,其中所有四边形都是正方形,所有的三角形都是直角三角形若正方形A、B、C、D的面积分别为3、5、2、3,则最大正方形E的面积是( )
A.47 B.13 C.11 D.8
10.若直角三角形中,斜边的长为17,一条直角边长为15,则另一条直角边长为( )
A.7 B.8 C.20 D.65
11.如图,在△ABC中,∠C=90°,AB=12,AC=6,则BC等于( )
A.6 B.6 C.6 D.12
12.如图,四边形ABCD中,∠A=90°,AD=2,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的值可能是( )
A. B.1 C. D.2
13.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为26和10,则正方形A的边长是( )
A.4 B.8 C.16 D.36
二.解答题
14.把两个同样大小的含45°角的三角尺,按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上,若AB=,求CD的长.
15.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高线.
(1)求证:AD垂直平分EF.
(2)若∠BAC=90°,直接写出图中所有的等腰直角三角形(不添加新的字母).
16.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,写出图中的直角三角形,并指出图中相等的锐角.
17.如图,在△ABC中,AC=BC,∠ACB=90°,D、E是边AB上的两点,AD=3,BE=4,∠DCE=45°,则△ABC的面积是多少?
18.如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
19.如图,BD,CE分别是△ABC的高,BD和CE相交于O.
(1)图中有哪几个直角三角形?
(2)图中有与∠2相等的角吗?请说明理由;
(3)若∠A=55°,∠ACB=65°,求∠3,∠4和∠5的度数.
参考答案
一.选择题
1. C.
2. B.
3. B.
4. A.
5. C.
6. C.
7. D.
8. B.
9. B.
10. B.
11. A.
12. D.
13. A.
二.解答题
14.解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BC=AB=2,BF=AF=AB=1,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=2,
在Rt△ADF中,根据勾股定理得,DF==,
∴CD=BF+DF﹣BC=1+﹣2=﹣1.
15.解:(1)∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,
在Rt△AED和Rt△AFD中,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,又DE=DF,
∴AD垂直平分EF;
(2)∵∠BAC=90°,AE=AF,
∴△AEF是等腰直角三角形,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠EAF=∠AFD=90°,
∴四边形AEDF是正方形,
∴∠EDF=90°,
∴△EDF是等腰直角三角形.
16.解:∵∠ACB=90°,
∴△ABC为直角三角形,
∵CD⊥AB,
∴△ADC、△BDC为直角三角形,
∴图中直角三角形有△ABC、△ADC、△BDC,
∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠CDB=∠ADB=90°,
∴∠BCD+∠B=90°,∠ACD+∠A=90°,
∴∠BCD=∠A,∠B=∠ACD.
17.解:∵AC=BC,∠ACB=90°,
∴∠ABC=∠CAB=45°,
设DE=x,则AB=AD+BE+DE=3+4+x=7+x,
∵∠DCE=∠CAE=∠DBC=45°,∠AEC=∠CED,∠BDC=∠CDE,
∴△ACE∽△CDE∽△BDC,
设CD=a,CE=b,
则有以下等式:
x:b=b:3+x,x:a=a:4+x,x:a=b:AC,
整理得,b2=x(x+3),a2=x(x+4),x?AC=ab,
则x2(x+3)(x+4)=a2b2=x2?AC2=,
解得,x=5;
∴AB=12,
∴AC=BC=6,
∴S△ABC=AC×BC=×6×6=36,
答:△ABC的面积是36.
18.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°﹣∠A=54°,
∴∠CBD=126°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=63°;
(2)∵∠ACB=90°,∠CBE=63°,
∴∠CEB=90°﹣63°=27°.
又∵∠F=27°,
∴∠F=∠CEB=27°,
∴DF∥BE
19.解:(1)∵BD,CE分别是△ABC的高,
∴∠ADB=∠CDB=∠AEC=∠BEC=90°,
∴图中有6个直角三角形,分别为△ABD、△CBD、△ACE、△BCE、△OBE、△OCD;
(2)图中有与∠2相等的角为∠1,理由如下:
∵∠2+∠A=90°,∠1+∠A=90°,
∴∠1=∠2;
(3)∵∠CDB=90°,∠ACB=65°,
∴∠3=90°﹣∠ACB=90°﹣65°=25°,
∵∠A=55°,∠ACB=65°,
∴∠ABC=180°﹣∠A﹣∠ACB=180°﹣55°﹣65°=60°,
∵∠BEC=90°,
∴∠4=90°﹣∠ABC=30°,
∴∠5=∠BOC=180°﹣∠3﹣∠4=180°﹣25°﹣30°=125°.
