2020-2021学年高一下学期物理教科版必修2第二章第三节圆周运动的实例分析 课件 16张PPT
文档属性
| 名称 | 2020-2021学年高一下学期物理教科版必修2第二章第三节圆周运动的实例分析 课件 16张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览





文档简介
圆圆周运动的实例分析
一.竖直平面内的圆周运动
G
G
N
N
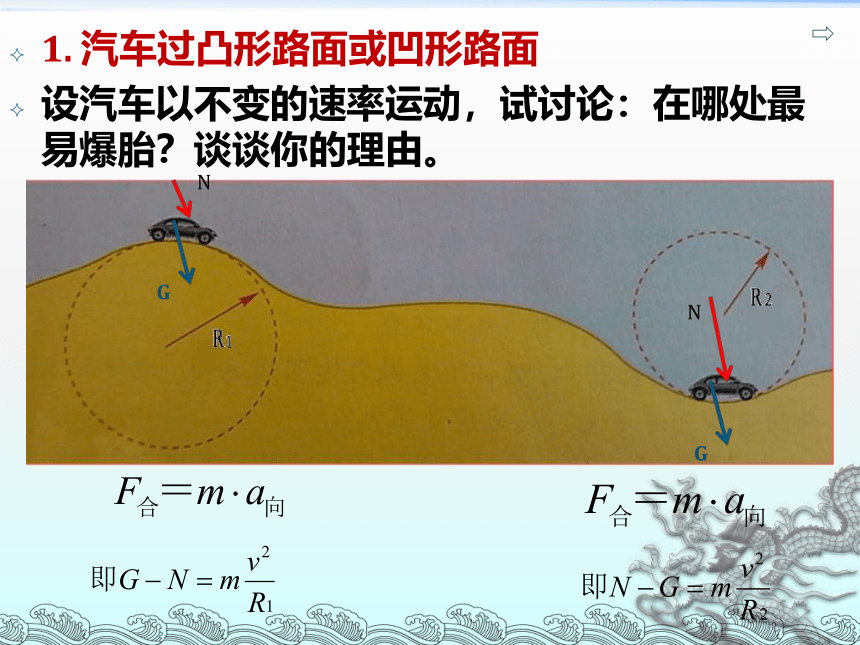
1. 汽车过凸形路面或凹形路面
设汽车以不变的速率运动,试讨论:在哪处最易爆胎?谈谈你的理由。
2.过山车
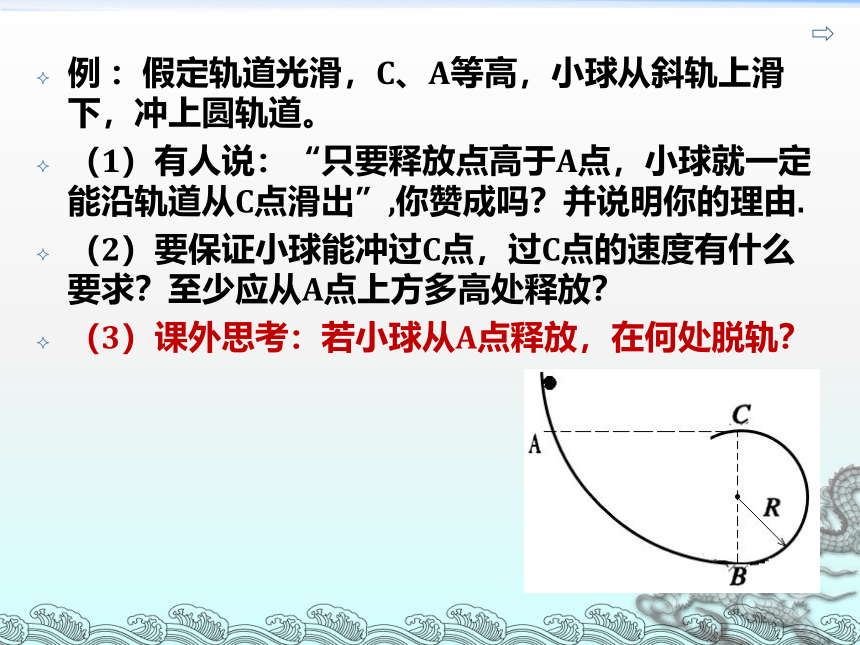
例 :假定轨道光滑,C、A等高,小球从斜轨上滑下,冲上圆轨道。
(1)有人说:“只要释放点高于A点,小球就一定能沿轨道从C点滑出”,你赞成吗?并说明你的理由.
(2)要保证小球能冲过C点,过C点的速度有什么要求?至少应从A点上方多高处释放?
(3)课外思考:若小球从A点释放,在何处脱轨?
3.绳拉小球情况
竖直平面内,长为L的细绳一端固定于O点,另一端系着一个小球,悬点正下方P点有一颗钉子。小球从与悬点等高处释放。
(1)讨论:“只要钉子低于释放点,小球就能做完整的圆运动”,你认为正确吗?
(2)忽略绳子碰钉子的能量损失,要让小球做完整的圆运动,钉子应距悬点多远?
二.圆锥摆运动
(1).旋转秋千
T
G
F合
θ
讨论:
小球匀速地作锥摆运动,若增大初速度,再次稳定地作锥摆运动,分析小球所受拉力T、线速度v、角速度ω有何变化?
如图,小球在光滑锥筒内做匀速圆周运动,
1.试分析其向心力是如何提供的?
2.若增大小球的线速度,再次稳定地做匀速圆周运动,试分析小球受的支持力、线速度、角速度如何变化?(设锥面与竖直轴线夹角为θ)
2.锥筒中小球的转动
N
G
F合
θ
3.火车转弯
拓展探究:
为适应国民经济的发展需要,从2007年4月18日起,我国铁路正式实施第六次提速,铁路相关系统进行了大量的技术更新。其中火车转弯技术的改进是重大课题。火车速度提高易使火车在转弯时外轨受损。
假设火车的运动可看成半径为R的圆周运动。设内外轨高度差为h,内外轨间距为d。已知重力加速度为g,h<(1)火车转弯所需的向心力是如何提供的?
(2)为什么高速转弯时,容易使外轨受损?
(3)为解决外轨受损这一难题,你认为理论上可采取哪些措施?
BD
N
G
F合
采取措施:
增加转弯半径
增大内外轨高度差
减小轨距
1.分析运动情景,明确研究对象,理想化为典型模型。
2.确定圆运动平面,找准圆心与半径,正确受力分析,弄清哪些力提供向心力;根据牛顿第二定律,建立向心力关系式,结合具体条件求解。
3. 圆周运动常与能量问题结合,要关注。
4.圆周运动经常涉及临界问题,挖掘隐含的临界条件是关键。
总结:分析圆周运动的基本方法和思想
(1)两根绳始终绷紧吗?
讨论交流
例.宇航员需要在离心实验器上做超重耐力训练。如图为某学生设计的训练宇航员的离心实验器:两根长度均为L的绳,拉直时与竖直方向的夹角60°,系在宇航员的座椅上。宇航员和椅子其总质量为m,在离心实验器转轴的带动下,宇航员沿水平面做匀速圆周运动。试分析:
(2)角速度ω达到何值时,两绳都有作用力?
一.竖直平面内的圆周运动
G
G
N
N
1. 汽车过凸形路面或凹形路面
设汽车以不变的速率运动,试讨论:在哪处最易爆胎?谈谈你的理由。
2.过山车
例 :假定轨道光滑,C、A等高,小球从斜轨上滑下,冲上圆轨道。
(1)有人说:“只要释放点高于A点,小球就一定能沿轨道从C点滑出”,你赞成吗?并说明你的理由.
(2)要保证小球能冲过C点,过C点的速度有什么要求?至少应从A点上方多高处释放?
(3)课外思考:若小球从A点释放,在何处脱轨?
3.绳拉小球情况
竖直平面内,长为L的细绳一端固定于O点,另一端系着一个小球,悬点正下方P点有一颗钉子。小球从与悬点等高处释放。
(1)讨论:“只要钉子低于释放点,小球就能做完整的圆运动”,你认为正确吗?
(2)忽略绳子碰钉子的能量损失,要让小球做完整的圆运动,钉子应距悬点多远?
二.圆锥摆运动
(1).旋转秋千
T
G
F合
θ
讨论:
小球匀速地作锥摆运动,若增大初速度,再次稳定地作锥摆运动,分析小球所受拉力T、线速度v、角速度ω有何变化?
如图,小球在光滑锥筒内做匀速圆周运动,
1.试分析其向心力是如何提供的?
2.若增大小球的线速度,再次稳定地做匀速圆周运动,试分析小球受的支持力、线速度、角速度如何变化?(设锥面与竖直轴线夹角为θ)
2.锥筒中小球的转动
N
G
F合
θ
3.火车转弯
拓展探究:
为适应国民经济的发展需要,从2007年4月18日起,我国铁路正式实施第六次提速,铁路相关系统进行了大量的技术更新。其中火车转弯技术的改进是重大课题。火车速度提高易使火车在转弯时外轨受损。
假设火车的运动可看成半径为R的圆周运动。设内外轨高度差为h,内外轨间距为d。已知重力加速度为g,h<
(2)为什么高速转弯时,容易使外轨受损?
(3)为解决外轨受损这一难题,你认为理论上可采取哪些措施?
BD
N
G
F合
采取措施:
增加转弯半径
增大内外轨高度差
减小轨距
1.分析运动情景,明确研究对象,理想化为典型模型。
2.确定圆运动平面,找准圆心与半径,正确受力分析,弄清哪些力提供向心力;根据牛顿第二定律,建立向心力关系式,结合具体条件求解。
3. 圆周运动常与能量问题结合,要关注。
4.圆周运动经常涉及临界问题,挖掘隐含的临界条件是关键。
总结:分析圆周运动的基本方法和思想
(1)两根绳始终绷紧吗?
讨论交流
例.宇航员需要在离心实验器上做超重耐力训练。如图为某学生设计的训练宇航员的离心实验器:两根长度均为L的绳,拉直时与竖直方向的夹角60°,系在宇航员的座椅上。宇航员和椅子其总质量为m,在离心实验器转轴的带动下,宇航员沿水平面做匀速圆周运动。试分析:
(2)角速度ω达到何值时,两绳都有作用力?
