2020-2021学年高一下学期物理教科版必修2第二章第三节圆周运动的实例分析 课件29张PPT
文档属性
| 名称 | 2020-2021学年高一下学期物理教科版必修2第二章第三节圆周运动的实例分析 课件29张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览



文档简介
高中物理教科版必修2第二章第三课
圆周运动的实例分析
3
圆周运动的实例分析
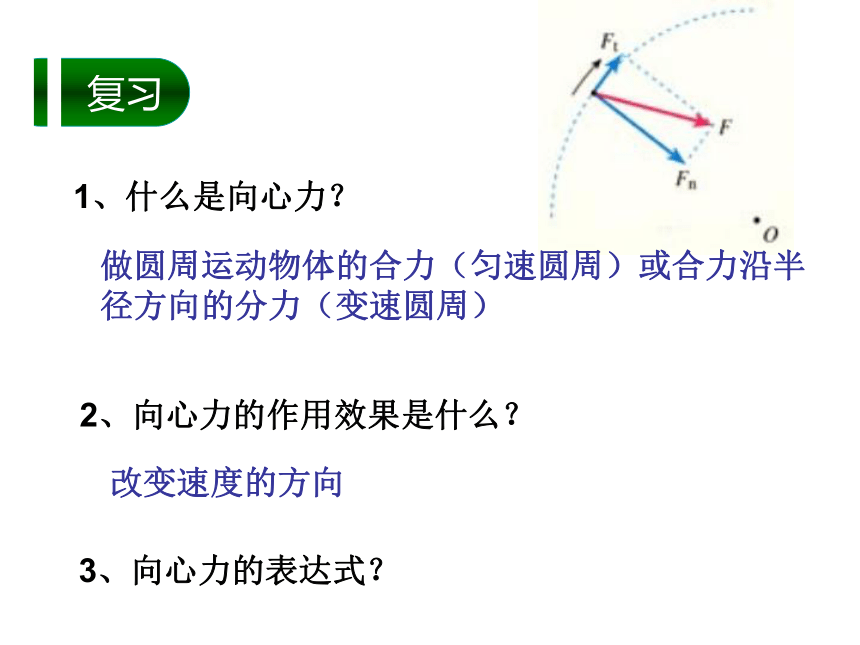
1、什么是向心力?
2、向心力的作用效果是什么?
3、向心力的表达式?
复习
做圆周运动物体的合力(匀速圆周)或合力沿半径方向的分力(变速圆周)
改变速度的方向
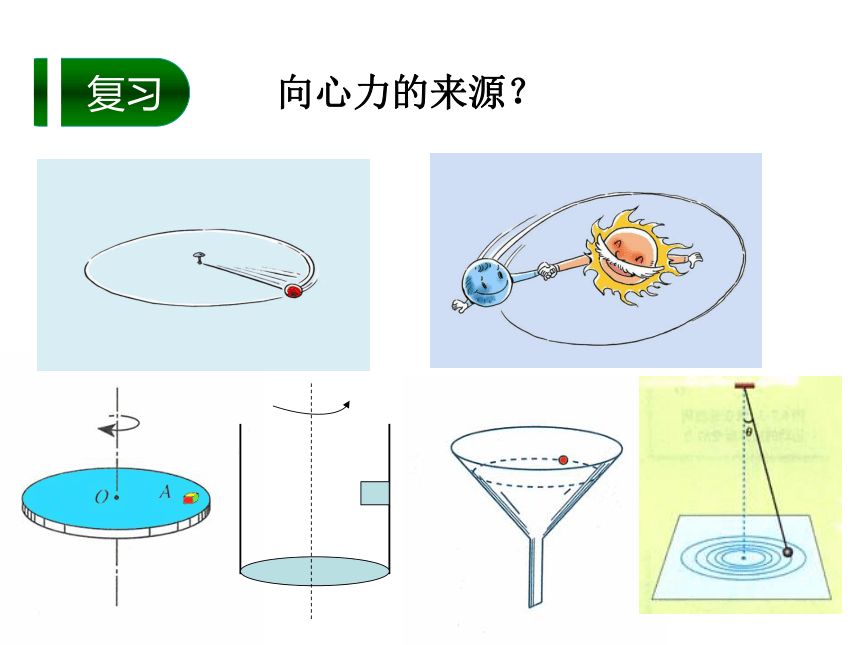
复习
向心力的来源?
“提供量”
向心力的来源
向心力和角速度、线速度、周期、半径之间的关系
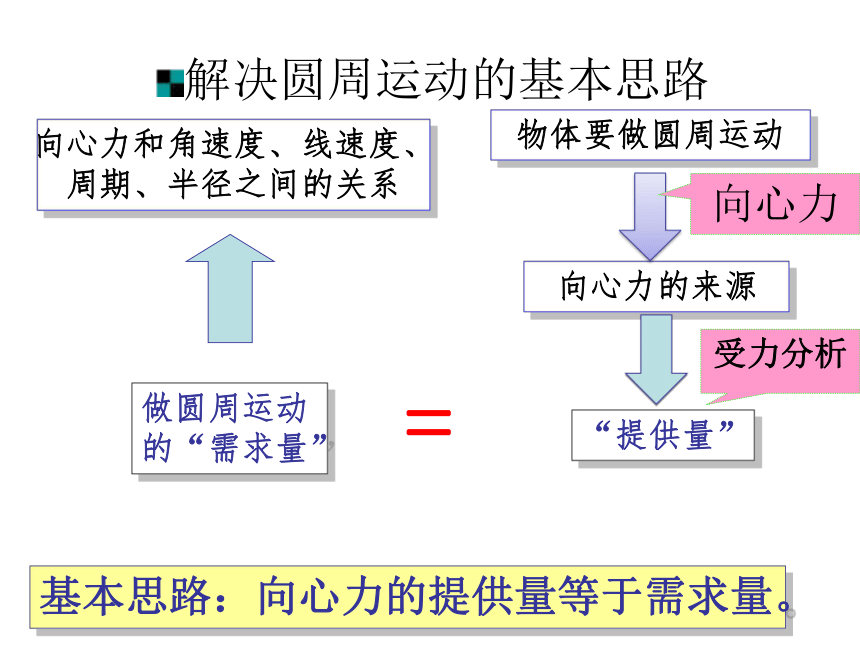
基本思路:向心力的提供量等于需求量。
解决圆周运动的基本思路
做圆周运动的“需求量”
=
物体要做圆周运动
向心力
受力分析
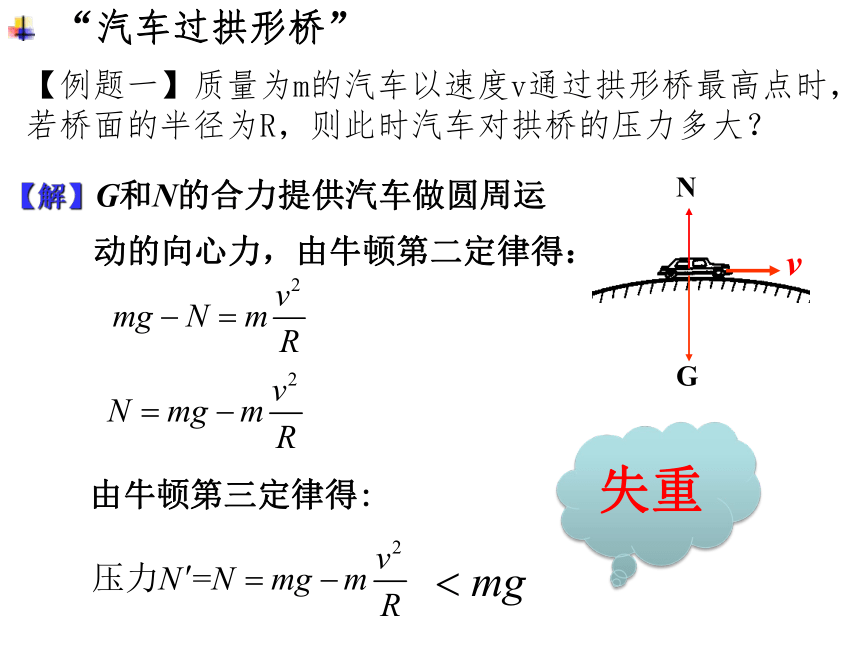
“汽车过拱形桥”
赵州桥是当今世界上现存最早、保存最完善的古代敞肩石拱桥。
【例题一】质量为m的汽车以速度v通过拱形桥最高点时,若桥面的半径为R,则此时汽车对拱桥的压力多大?
【解】G和N的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
由牛顿第三定律得:
N
G
失重
“汽车过拱形桥”
N
G
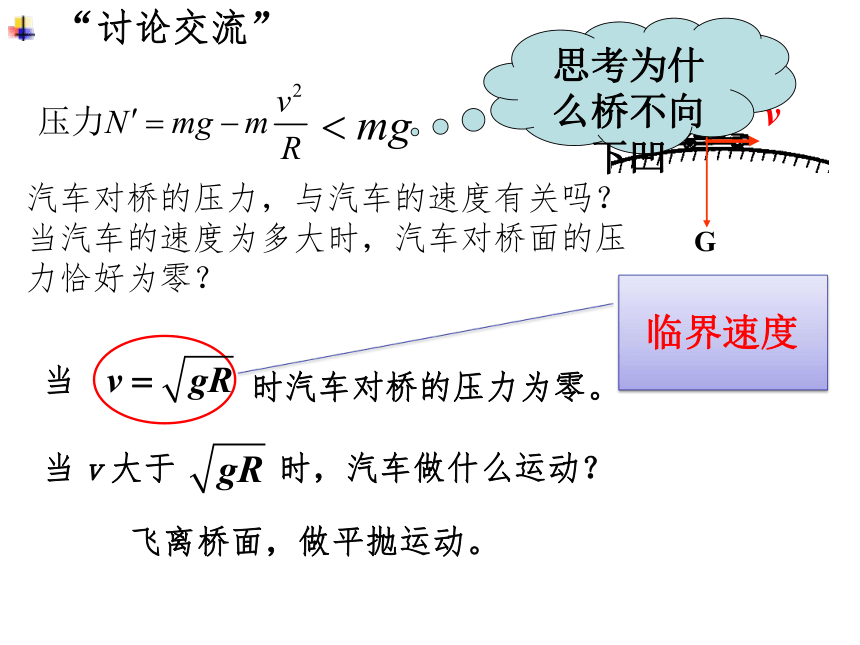
汽车对桥的压力,与汽车的速度有关吗?当汽车的速度为多大时,汽车对桥面的压力恰好为零?
当
时汽车对桥的压力为零。
当v大于 时,汽车做什么运动?
临界速度
“讨论交流”
飞离桥面,做平抛运动。
思考为什么桥不向下凹
B
mg
mg
N
A
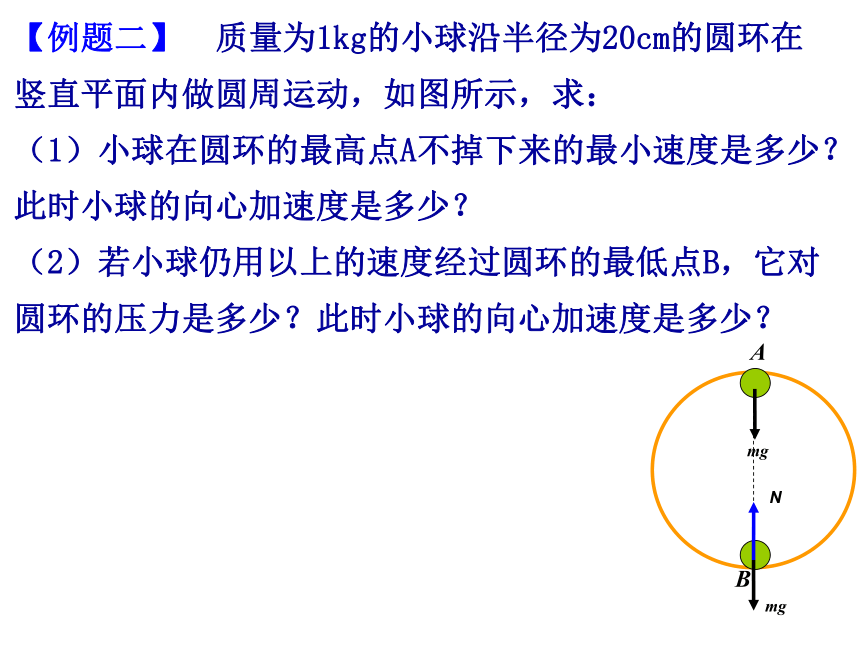
【例题二】 质量为1kg的小球沿半径为20cm的圆环在竖直平面内做圆周运动,如图所示,求:
(1)小球在圆环的最高点A不掉下来的最小速度是多少?此时小球的向心加速度是多少?
(2)若小球仍用以上的速度经过圆环的最低点B,它对圆环的压力是多少?此时小球的向心加速度是多少?
解:(1)若小球重力刚好提供做圆周运动的向心力,轨道对小球无弹力,此时的速度为最小速度。由牛顿第二定律:
解得:
向心加速度
(2)小球以该速度经过B点时,由牛顿第二定律:
解得:N=20N
由牛顿第三定律:它对圆环的压力为20N。
此时向心加速度
B
mg
mg
N
A
“旋转秋千”
“旋转秋千”
【例题三】 已知物理量如图所示,请计算小球做匀速圆周运动的角速度。
解:由牛顿第二定律得,
由几何关系有,
解得,
h是悬点到圆心的距离。
由圆锥摆模型解决旋转秋千的问题
试试看:
1、若角速度增大,会发生什么变化?
2、体重不同的人坐在秋千上旋转时,缆绳与中心轴的夹角一样吗?
3、请推出它的周期公式。
当火车转弯时,分析火车的受力情况?火车转弯时所需要的向心力由什么力提供呢?
火车转弯
请分析火车做匀速直线运动受力情况?
a.内外轨道等高
N
G
火车转弯
内轨
外轨
F
火车挤压 (外轨、内轨),获得一个反作用力,充当向心力。
轮缘与外轨间的相互作用力太大,铁轨和车轮极易受损!
火车速度为30m/s,弯道的半径R=900m,火车的质量m=8×105kg,转弯时轮缘对轨道侧向的弹力多大?
N
G
讨论
应该如何解决这一实际问题
N
G
让外轨高于内轨道,使支持力的方向发生改变。支持力和重力的合力充当向心力。
运动轨迹在水平面内!
重力和支持力的合力提供向心力,方向水平指向圆心。
FN
G
F
θ
θ
h是内外轨高度差,L是轨距
G
N
h
L
?
Fn
注意这时的向心力是水平的
?
?
Fn=mgtanα≈mgsinα=mgh/L
(4)设计时速
汽车转弯
如果汽车的速度很大,会出现什么情况呢?
有什么解决措施?
摩托车转弯
飞机转弯
当F合= F,做圆周运动
当F合< F,
供 :指向圆心的合力
需 :
当F合> F,做向心运动
做离心运动
离心运动
在做圆周运动时,由于合外力提供的向心力消失或不足,以致物体沿圆周运动的切线方向飞出或远离圆心而去的运动叫做离心运动。
4、离心运动的应用和防止
(1)洗衣机的脱水筒
(2)离心干燥器的金属网笼
(3)用离心机把体温计的水银柱甩回玻璃泡内
(4)弯道限速
4、离心运动本质:
离心现象的本质是物体惯性的表现;
离心运动是物体逐渐远离圆心的一种物理现象。
5、离心运动的特点 :
做圆周运动的质点,当合外力消失时,它就以这一时刻的线速度沿切线方向飞去.
做离心运动的质点不存在所谓的“离心力”作用,因为没有任何物体提供这种力 .
圆周运动的实例分析
3
圆周运动的实例分析
1、什么是向心力?
2、向心力的作用效果是什么?
3、向心力的表达式?
复习
做圆周运动物体的合力(匀速圆周)或合力沿半径方向的分力(变速圆周)
改变速度的方向
复习
向心力的来源?
“提供量”
向心力的来源
向心力和角速度、线速度、周期、半径之间的关系
基本思路:向心力的提供量等于需求量。
解决圆周运动的基本思路
做圆周运动的“需求量”
=
物体要做圆周运动
向心力
受力分析
“汽车过拱形桥”
赵州桥是当今世界上现存最早、保存最完善的古代敞肩石拱桥。
【例题一】质量为m的汽车以速度v通过拱形桥最高点时,若桥面的半径为R,则此时汽车对拱桥的压力多大?
【解】G和N的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
由牛顿第三定律得:
N
G
失重
“汽车过拱形桥”
N
G
汽车对桥的压力,与汽车的速度有关吗?当汽车的速度为多大时,汽车对桥面的压力恰好为零?
当
时汽车对桥的压力为零。
当v大于 时,汽车做什么运动?
临界速度
“讨论交流”
飞离桥面,做平抛运动。
思考为什么桥不向下凹
B
mg
mg
N
A
【例题二】 质量为1kg的小球沿半径为20cm的圆环在竖直平面内做圆周运动,如图所示,求:
(1)小球在圆环的最高点A不掉下来的最小速度是多少?此时小球的向心加速度是多少?
(2)若小球仍用以上的速度经过圆环的最低点B,它对圆环的压力是多少?此时小球的向心加速度是多少?
解:(1)若小球重力刚好提供做圆周运动的向心力,轨道对小球无弹力,此时的速度为最小速度。由牛顿第二定律:
解得:
向心加速度
(2)小球以该速度经过B点时,由牛顿第二定律:
解得:N=20N
由牛顿第三定律:它对圆环的压力为20N。
此时向心加速度
B
mg
mg
N
A
“旋转秋千”
“旋转秋千”
【例题三】 已知物理量如图所示,请计算小球做匀速圆周运动的角速度。
解:由牛顿第二定律得,
由几何关系有,
解得,
h是悬点到圆心的距离。
由圆锥摆模型解决旋转秋千的问题
试试看:
1、若角速度增大,会发生什么变化?
2、体重不同的人坐在秋千上旋转时,缆绳与中心轴的夹角一样吗?
3、请推出它的周期公式。
当火车转弯时,分析火车的受力情况?火车转弯时所需要的向心力由什么力提供呢?
火车转弯
请分析火车做匀速直线运动受力情况?
a.内外轨道等高
N
G
火车转弯
内轨
外轨
F
火车挤压 (外轨、内轨),获得一个反作用力,充当向心力。
轮缘与外轨间的相互作用力太大,铁轨和车轮极易受损!
火车速度为30m/s,弯道的半径R=900m,火车的质量m=8×105kg,转弯时轮缘对轨道侧向的弹力多大?
N
G
讨论
应该如何解决这一实际问题
N
G
让外轨高于内轨道,使支持力的方向发生改变。支持力和重力的合力充当向心力。
运动轨迹在水平面内!
重力和支持力的合力提供向心力,方向水平指向圆心。
FN
G
F
θ
θ
h是内外轨高度差,L是轨距
G
N
h
L
?
Fn
注意这时的向心力是水平的
?
?
Fn=mgtanα≈mgsinα=mgh/L
(4)设计时速
汽车转弯
如果汽车的速度很大,会出现什么情况呢?
有什么解决措施?
摩托车转弯
飞机转弯
当F合= F,做圆周运动
当F合< F,
供 :指向圆心的合力
需 :
当F合> F,做向心运动
做离心运动
离心运动
在做圆周运动时,由于合外力提供的向心力消失或不足,以致物体沿圆周运动的切线方向飞出或远离圆心而去的运动叫做离心运动。
4、离心运动的应用和防止
(1)洗衣机的脱水筒
(2)离心干燥器的金属网笼
(3)用离心机把体温计的水银柱甩回玻璃泡内
(4)弯道限速
4、离心运动本质:
离心现象的本质是物体惯性的表现;
离心运动是物体逐渐远离圆心的一种物理现象。
5、离心运动的特点 :
做圆周运动的质点,当合外力消失时,它就以这一时刻的线速度沿切线方向飞去.
做离心运动的质点不存在所谓的“离心力”作用,因为没有任何物体提供这种力 .
