初中数学鲁教版七年级下册第八章3基本事实与定理练习题(Word版 含解析)
文档属性
| 名称 | 初中数学鲁教版七年级下册第八章3基本事实与定理练习题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 38.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 15:13:01 | ||
图片预览




文档简介
初中数学鲁教版七年级下册第八章3基本事实与定理练习题
一、选择题
下列四个命题中,真命题有
两条直线被第三条直线所截,内错角相等;
如果和是对顶角,那么;
如果、,那么;
平方等于4的数是2.
A.
1个
B.
2个
C.
3个
D.
4个
下列命题是假命题的是
A.
平行四边形是中心对称图形
B.
对角线垂直且相等的四边形是正方形
C.
五边形的内角和为
D.
矩形的对角线相等
给出下列命题:有一个角为的等腰三角形是等边三角形;三个内角度数之比为1:2:3的三角形是直角三角形:有三条互不重合的直线a,b,c,若,,那么;等腰三角形两条边的长度分别为2和4,则它的周长为8或10.
其中真命题的个数为
A.
4个
B.
3个
C.
2个
D.
1个
下列命题的逆命题是真命题的是
A.
若,则
B.
同位角相等,两直线平行
C.
对顶角相等
D.
若,,则
下列说法正确的是
A.
一个命题一定有逆命题
B.
一个定理一定有逆定理
C.
真命题的逆命题一定是真命题
D.
假命题的逆命题一定是假命题
已知下列命题:其中原命题与逆命题均为真命题的个数是
若,则;
若,则;
等边三角形的三个内角都相等;
底角相等的两个等腰三角形全等.
A.
1个
B.
2个
C.
3个
D.
4个
下列命题中,属于假命题的是
A.
直角三角形的两个锐角互余
B.
有一个角是的三角形是等边三角形
C.
两点之间线段最短
D.
对顶角相等
有下列四个命题:
直径是圆中最长的弦;
半圆是弧;
平分弦的直径垂直于弦;
以圆中任意两条直径为对角线的四边形是矩形.
其中真命题有
A.
1个
B.
2个
C.
3个
D.
4个
下列命题写出逆命题之后,两者互为逆定理的是
A.
全等三角形的面积相等
B.
若两个角都是直角,则它们相等
C.
两直线平行,同位角相等
D.
若,则
下列命题中正确的是
A.
如果两个角相等,那么这两个角一定是对顶角
B.
如果两个角互为补角,那么这两个角一定是邻补角
C.
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
D.
如果两条平行线被第三条直线所截,那么同旁内角相等
二、填空题
“直角都相等“的逆命题是______
.
“对顶角相等”是一个______命题填“真”或“假”.
命题“平行于同一直线的两条直线平行”的条件是______;结论是______;这个命题是______命题填“真”或“假”.
命题“正方形的四条边相等”的逆命题是______,它是______填“真命题”或“假命题”.
三、解答题
下列各命题都成立,写出它们的逆命题,这些逆命题成立吗?
同旁内角互补,两直线平行.
如果两个角是直角,那么这两个角相等.
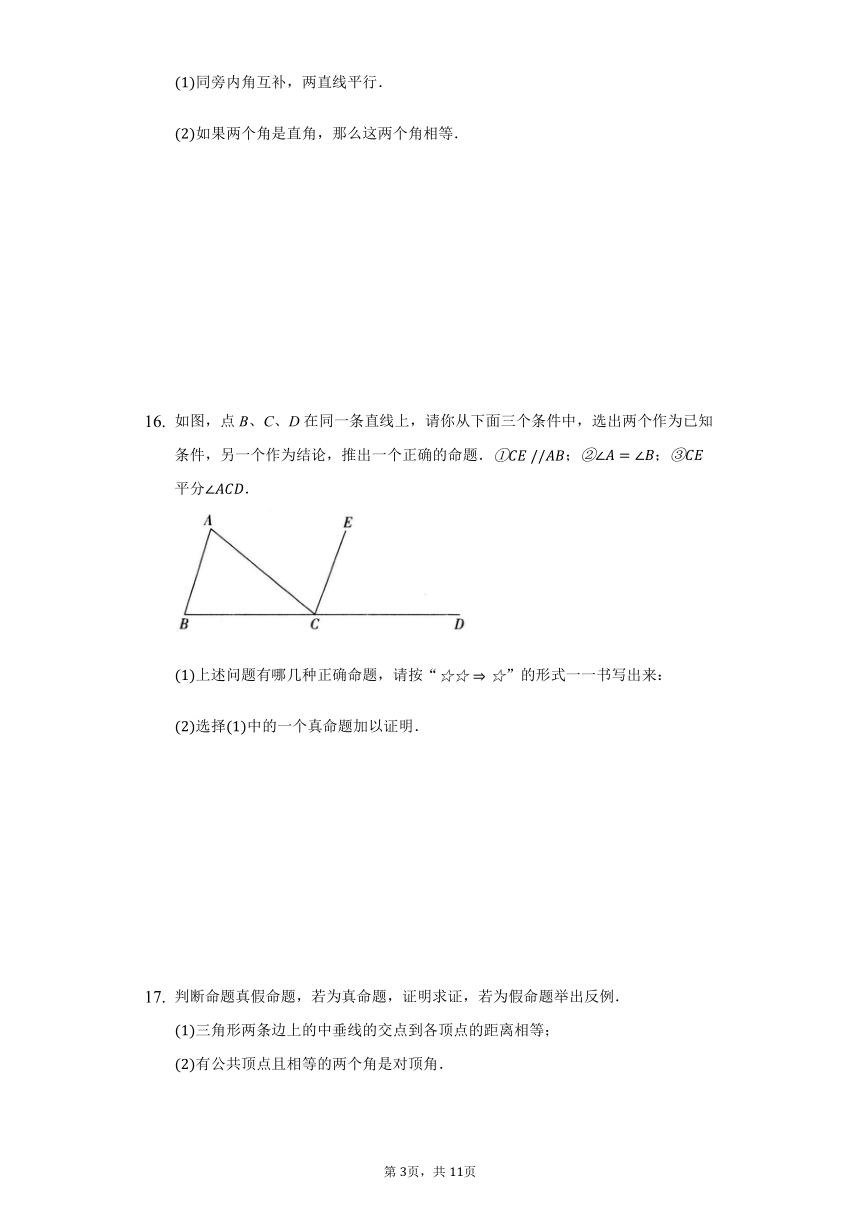
如图,点B、C、D在同一条直线上,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.;;平分.
上述问题有哪几种正确命题,请按“”的形式一一书写出来:
选择中的一个真命题加以证明.
判断命题真假命题,若为真命题,证明求证,若为假命题举出反例.
三角形两条边上的中垂线的交点到各顶点的距离相等;
有公共顶点且相等的两个角是对顶角.
判断下列命题的真假:
一个三角形如果有两个内角互余,那么这个三角形是直角三角形;
如果,那么;
同角的补角相等;
两个无理数的和仍是无理数.
答案和解析
1.【答案】B
【解析】解:两条平行直线被第三条直线所截,内错角相等,所以为假命题;
如果和是对顶角,那么,所以为真命题;
如果、,那么,所以为真命题;
平方等于4的数是2或,所以为假命题.
故选:B.
根据平行线的性质对进行判断;根据对顶角的性质对进行判断;根据两负数的和仍然为负数可对进行判断;根据平方根的定义对进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
2.【答案】B
【解析】解:A、平行四边形是中心对称图形,是真命题;
B、对角线平分、垂直且相等的四边形是正方形,原命题是假命题;
C、五边形的内角和为,是真命题;
D、矩形的对角线相等,是真命题;
故选:B.
根据平行四边形、正方形、五边形和矩形的性质判断即可.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
3.【答案】B
【解析】解:有一个角为的等腰三角形是等边三角形,是真命题.
三个内角度数之比为1:2:3的三角形是直角三角形,是真命题.
有三条互不重合的直线a,b,c,若,,那么,是真命题.
等腰三角形两条边的长度分别为2和4,则它的周长为8或10,是假命题.
其中真命题的个数为3,
故选:B.
根据等边三角形的判定,等腰三角形的性质,平行线的判定等知识一一判断即可.
本题考查等边三角形的判定,等腰三角形的性质,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.【答案】B
【解析】解:A、若,则的逆命题是若,则,逆命题是假命题,不符合题意;
B、同位角相等,两直线平行的逆命题是两直线平行,同位角相等,逆命题是真命题,符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
D、若,,则的逆命题是若,则,,逆命题是假命题,不符合题意;
故选:B.
分别写出原命题的逆命题,然后判断真假即可.
考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题,难度不大.
5.【答案】A
【解析】解:A、一个命题一定有逆命题,正确,符合题意;
B、定理的逆命题不一定是真命题,故错误,不符合题意;
C、真命题的逆命题不一定是真命题,故错误,不符合题意;
D、假命题的逆命题也有可能是真命题,故错误,不符合题意,
故选:A.
根据互逆命题的定义对A进行判断;根据命题与逆命题的真假没有联系可对B、C、D进行判断.
本题考查了命题与定理:断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式.2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.
6.【答案】A
【解析】解:若,则,此命题为假命题,它的逆命题为若,则,此逆命题为假命题;
若,则,此命题为真命题,它的逆命题为若,则,此逆命题为假命题;
等边三角形的三个内角都相等,此命题为真命题,它的逆命题为三个内角相等的三角形为等边三角形,此逆命题为真命题;
底角相等的两个等腰三角形全等,此命题为假命题,它的逆命题为全等的两个等腰三角形的底角相等,此逆命题为真命题.
故选:A.
先交换各命题的题设与结论,然后根据不等式的性质、绝对值的意义、等边三角形的判定与性质、全等三角形的判定和性质对各命题和它们的逆命题进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
7.【答案】B
【解析】解:A、直角三角形的两个锐角互余,是真命题;
B、有一个角是的等腰三角形是等边三角形,原命题是假命题;
C、两点之间线段最短,是真命题;
D、对顶角相等,是真命题;
故选:B.
根据对顶角、等边三角形的性质、线段的性质和三角形内角和解答即可.
本题考查了命题与定理的知识,解题的关键是了解对顶角、等边三角形的性质、线段的性质和三角形内角和,难度不大.
8.【答案】C
【解析】解:直径是圆中最长的弦,正确,是真命题,符合题意;
半圆是弧,正确,是真命题,符合题意;
平分弦不是直径的直径垂直于弦,故原命题错误,不符合题意;
根据对角线相等且相互平分的四边形是矩形可判断此命题正确,是真命题,符合题意,
真命题有3个,
故选:C.
利用圆的有关性质及定理、矩形的判定等知识分别判断后即可确定正确的选项.
考查了命题与定理的知识,解题的关键是了解圆的有关性质及定理、矩形的判定等知识,难度不大.
9.【答案】C
【解析】解:A、逆命题为:面积相等的三角形全等,错误,是假命题,不符合题意;
B、逆命题为:相等的两个角是直角,错误,是假命题,不符合题意;
C、逆命题为:同位角相等,两直线平行,正确,与原命题互为逆定理,符合题意;
D、逆命题为:若,则,错误,为假命题,不符合题意,
故选:C.
写出原命题的逆命题后判断正误即可确定正确的选项.
考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题并判断正误,难度不大.
10.【答案】C
【解析】解:A、如果两个角相等,那么这两个角一定是对顶角,这个命题为假命题;
B、如果两个角互为补角,那么这两个角一定是邻补角,这个命题为假命题;
C、如果两条直线都与第三条直线平行,那么这两条直线也互相平行,这个命题为真命题;
D、如果两条平行线被第三条直线所截,那么同旁内角相等,这个命题为假命题.
故选:C.
根据对顶角的定义对A进行判断;根据邻补角的定义对B进行判断;根据平行线的传递性对C进行判断;根据平行线的性质对D进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
11.【答案】如果两个角相等,那么这两个角都是直角
【解析】解:直角都相等的逆命题是:如果两个角相等,那么这两个角都是直角.
故答案为:如果两个角相等,那么这两个角都是直角
根据逆命题的概念解答即可.
本题考查的是命题和定理,掌握两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题是解题的关键.
12.【答案】真
【解析】解:对顶角相等是真命题,
故答案为:真.
根据对顶角相等、真命题的概念解答.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
13.【答案】两条直线平行于同一条直线?
这两条直线平行?
真
【解析】解:命题“平行于同一直线的两条直线平行”的条件是两条直线平行于同一条直线;结论是这两条直线平行;这个命题是真命题.
故答案为两条直线平行于同一条直线,这两条直线平行,真.
利用命题由题设和结论两部分组成,命题“平行于同一直线的两条直线平行”的题设部分为两条直线平行于同一条直线;结论部分为这两条直线平行;根据平行线的性质可判断此命题为真命题.
本题考查了命题与定理:判断事物的语句叫命题,命题由题设和结论两部分组成;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.也考查了逆命题.
14.【答案】四条边相等的四边形是正方形?
假
【解析】解:命题“正方形的四条边相等”的逆命题是“四条边相等的四边形是正方形”,
它是假命题,
故答案为:四条边相等的四边形是正方形;假.
根据逆命题的概念写出原命题的逆命题,根据正方形的判定定理判断即可.
本题考查的是命题的真假判断、逆命题的概念,掌握正方形的判定定理是解题的关键.
15.【答案】解:同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立;
如果两个角是直角,那么这两个角相等的逆命题是如果两个角相等、那么这两个角是直角,不成立.
【解析】分别写出两个命题的逆命题,根据平行线的性质、角的定义判断即可.
本题考查的是命题的真假判断、逆命题的概念,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.
16.【答案】解:上述问题有三种正确命题,分别是:
命题1:;命题2:;命题3:.
解:选择命题2:.
证明:,,.
平分,.
.
【解析】根据题意,结合平行线的性质,选择两个条件做题设,一个条件做结论,得到正确的命题;任选一个命题,根据平行线的性质或角平分线的定义进行证明.
本题考查的是平行线的性质以及角平分线的性质,本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.
17.【答案】解:三角形两条边上的中垂线的交点到各顶点的距离相等;真命题;理由如下:
如图,
是线段AB和线段AC的垂直平分线的交点,
,,
,
三角形两条边上的中垂线的交点到各顶点的距离相等;
有公共顶点且相等的两个角是对顶角;假命题;理由如下:
两条直线相交所形成的角中相对的角是对顶角,
例如,平角的角平分线把平角分为两个直角,这两个直角不是对顶角,
是假命题.
【解析】由线段垂直平分线的性质即可得出结论;
由对顶角定义进行判断即可.
本题考查的是命题的证明,熟练掌握线段垂直平分线的性质、对顶角定义是解题的关键.
18.【答案】解:一个三角形如果有两个内角互余,那么这个三角形是直角三角形,此命题为真命题;
当,,则,所以命题“如果,那么”为假命题;
同角的补角相等,此命题为真命题;
两无理数为和,它们的和为0,命题“两个无理数的和仍是无理数”为假命题.
【解析】利用三角形内角和和互余的定义对进行判断;
利用反例进行判断;
根据补角的定义进行判断;
利用反例进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
第2页,共2页
第1页,共1页
一、选择题
下列四个命题中,真命题有
两条直线被第三条直线所截,内错角相等;
如果和是对顶角,那么;
如果、,那么;
平方等于4的数是2.
A.
1个
B.
2个
C.
3个
D.
4个
下列命题是假命题的是
A.
平行四边形是中心对称图形
B.
对角线垂直且相等的四边形是正方形
C.
五边形的内角和为
D.
矩形的对角线相等
给出下列命题:有一个角为的等腰三角形是等边三角形;三个内角度数之比为1:2:3的三角形是直角三角形:有三条互不重合的直线a,b,c,若,,那么;等腰三角形两条边的长度分别为2和4,则它的周长为8或10.
其中真命题的个数为
A.
4个
B.
3个
C.
2个
D.
1个
下列命题的逆命题是真命题的是
A.
若,则
B.
同位角相等,两直线平行
C.
对顶角相等
D.
若,,则
下列说法正确的是
A.
一个命题一定有逆命题
B.
一个定理一定有逆定理
C.
真命题的逆命题一定是真命题
D.
假命题的逆命题一定是假命题
已知下列命题:其中原命题与逆命题均为真命题的个数是
若,则;
若,则;
等边三角形的三个内角都相等;
底角相等的两个等腰三角形全等.
A.
1个
B.
2个
C.
3个
D.
4个
下列命题中,属于假命题的是
A.
直角三角形的两个锐角互余
B.
有一个角是的三角形是等边三角形
C.
两点之间线段最短
D.
对顶角相等
有下列四个命题:
直径是圆中最长的弦;
半圆是弧;
平分弦的直径垂直于弦;
以圆中任意两条直径为对角线的四边形是矩形.
其中真命题有
A.
1个
B.
2个
C.
3个
D.
4个
下列命题写出逆命题之后,两者互为逆定理的是
A.
全等三角形的面积相等
B.
若两个角都是直角,则它们相等
C.
两直线平行,同位角相等
D.
若,则
下列命题中正确的是
A.
如果两个角相等,那么这两个角一定是对顶角
B.
如果两个角互为补角,那么这两个角一定是邻补角
C.
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
D.
如果两条平行线被第三条直线所截,那么同旁内角相等
二、填空题
“直角都相等“的逆命题是______
.
“对顶角相等”是一个______命题填“真”或“假”.
命题“平行于同一直线的两条直线平行”的条件是______;结论是______;这个命题是______命题填“真”或“假”.
命题“正方形的四条边相等”的逆命题是______,它是______填“真命题”或“假命题”.
三、解答题
下列各命题都成立,写出它们的逆命题,这些逆命题成立吗?
同旁内角互补,两直线平行.
如果两个角是直角,那么这两个角相等.
如图,点B、C、D在同一条直线上,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.;;平分.
上述问题有哪几种正确命题,请按“”的形式一一书写出来:
选择中的一个真命题加以证明.
判断命题真假命题,若为真命题,证明求证,若为假命题举出反例.
三角形两条边上的中垂线的交点到各顶点的距离相等;
有公共顶点且相等的两个角是对顶角.
判断下列命题的真假:
一个三角形如果有两个内角互余,那么这个三角形是直角三角形;
如果,那么;
同角的补角相等;
两个无理数的和仍是无理数.
答案和解析
1.【答案】B
【解析】解:两条平行直线被第三条直线所截,内错角相等,所以为假命题;
如果和是对顶角,那么,所以为真命题;
如果、,那么,所以为真命题;
平方等于4的数是2或,所以为假命题.
故选:B.
根据平行线的性质对进行判断;根据对顶角的性质对进行判断;根据两负数的和仍然为负数可对进行判断;根据平方根的定义对进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
2.【答案】B
【解析】解:A、平行四边形是中心对称图形,是真命题;
B、对角线平分、垂直且相等的四边形是正方形,原命题是假命题;
C、五边形的内角和为,是真命题;
D、矩形的对角线相等,是真命题;
故选:B.
根据平行四边形、正方形、五边形和矩形的性质判断即可.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
3.【答案】B
【解析】解:有一个角为的等腰三角形是等边三角形,是真命题.
三个内角度数之比为1:2:3的三角形是直角三角形,是真命题.
有三条互不重合的直线a,b,c,若,,那么,是真命题.
等腰三角形两条边的长度分别为2和4,则它的周长为8或10,是假命题.
其中真命题的个数为3,
故选:B.
根据等边三角形的判定,等腰三角形的性质,平行线的判定等知识一一判断即可.
本题考查等边三角形的判定,等腰三角形的性质,平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.【答案】B
【解析】解:A、若,则的逆命题是若,则,逆命题是假命题,不符合题意;
B、同位角相等,两直线平行的逆命题是两直线平行,同位角相等,逆命题是真命题,符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
D、若,,则的逆命题是若,则,,逆命题是假命题,不符合题意;
故选:B.
分别写出原命题的逆命题,然后判断真假即可.
考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题,难度不大.
5.【答案】A
【解析】解:A、一个命题一定有逆命题,正确,符合题意;
B、定理的逆命题不一定是真命题,故错误,不符合题意;
C、真命题的逆命题不一定是真命题,故错误,不符合题意;
D、假命题的逆命题也有可能是真命题,故错误,不符合题意,
故选:A.
根据互逆命题的定义对A进行判断;根据命题与逆命题的真假没有联系可对B、C、D进行判断.
本题考查了命题与定理:断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式.2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.
6.【答案】A
【解析】解:若,则,此命题为假命题,它的逆命题为若,则,此逆命题为假命题;
若,则,此命题为真命题,它的逆命题为若,则,此逆命题为假命题;
等边三角形的三个内角都相等,此命题为真命题,它的逆命题为三个内角相等的三角形为等边三角形,此逆命题为真命题;
底角相等的两个等腰三角形全等,此命题为假命题,它的逆命题为全等的两个等腰三角形的底角相等,此逆命题为真命题.
故选:A.
先交换各命题的题设与结论,然后根据不等式的性质、绝对值的意义、等边三角形的判定与性质、全等三角形的判定和性质对各命题和它们的逆命题进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
7.【答案】B
【解析】解:A、直角三角形的两个锐角互余,是真命题;
B、有一个角是的等腰三角形是等边三角形,原命题是假命题;
C、两点之间线段最短,是真命题;
D、对顶角相等,是真命题;
故选:B.
根据对顶角、等边三角形的性质、线段的性质和三角形内角和解答即可.
本题考查了命题与定理的知识,解题的关键是了解对顶角、等边三角形的性质、线段的性质和三角形内角和,难度不大.
8.【答案】C
【解析】解:直径是圆中最长的弦,正确,是真命题,符合题意;
半圆是弧,正确,是真命题,符合题意;
平分弦不是直径的直径垂直于弦,故原命题错误,不符合题意;
根据对角线相等且相互平分的四边形是矩形可判断此命题正确,是真命题,符合题意,
真命题有3个,
故选:C.
利用圆的有关性质及定理、矩形的判定等知识分别判断后即可确定正确的选项.
考查了命题与定理的知识,解题的关键是了解圆的有关性质及定理、矩形的判定等知识,难度不大.
9.【答案】C
【解析】解:A、逆命题为:面积相等的三角形全等,错误,是假命题,不符合题意;
B、逆命题为:相等的两个角是直角,错误,是假命题,不符合题意;
C、逆命题为:同位角相等,两直线平行,正确,与原命题互为逆定理,符合题意;
D、逆命题为:若,则,错误,为假命题,不符合题意,
故选:C.
写出原命题的逆命题后判断正误即可确定正确的选项.
考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题并判断正误,难度不大.
10.【答案】C
【解析】解:A、如果两个角相等,那么这两个角一定是对顶角,这个命题为假命题;
B、如果两个角互为补角,那么这两个角一定是邻补角,这个命题为假命题;
C、如果两条直线都与第三条直线平行,那么这两条直线也互相平行,这个命题为真命题;
D、如果两条平行线被第三条直线所截,那么同旁内角相等,这个命题为假命题.
故选:C.
根据对顶角的定义对A进行判断;根据邻补角的定义对B进行判断;根据平行线的传递性对C进行判断;根据平行线的性质对D进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
11.【答案】如果两个角相等,那么这两个角都是直角
【解析】解:直角都相等的逆命题是:如果两个角相等,那么这两个角都是直角.
故答案为:如果两个角相等,那么这两个角都是直角
根据逆命题的概念解答即可.
本题考查的是命题和定理,掌握两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题是解题的关键.
12.【答案】真
【解析】解:对顶角相等是真命题,
故答案为:真.
根据对顶角相等、真命题的概念解答.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
13.【答案】两条直线平行于同一条直线?
这两条直线平行?
真
【解析】解:命题“平行于同一直线的两条直线平行”的条件是两条直线平行于同一条直线;结论是这两条直线平行;这个命题是真命题.
故答案为两条直线平行于同一条直线,这两条直线平行,真.
利用命题由题设和结论两部分组成,命题“平行于同一直线的两条直线平行”的题设部分为两条直线平行于同一条直线;结论部分为这两条直线平行;根据平行线的性质可判断此命题为真命题.
本题考查了命题与定理:判断事物的语句叫命题,命题由题设和结论两部分组成;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.也考查了逆命题.
14.【答案】四条边相等的四边形是正方形?
假
【解析】解:命题“正方形的四条边相等”的逆命题是“四条边相等的四边形是正方形”,
它是假命题,
故答案为:四条边相等的四边形是正方形;假.
根据逆命题的概念写出原命题的逆命题,根据正方形的判定定理判断即可.
本题考查的是命题的真假判断、逆命题的概念,掌握正方形的判定定理是解题的关键.
15.【答案】解:同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立;
如果两个角是直角,那么这两个角相等的逆命题是如果两个角相等、那么这两个角是直角,不成立.
【解析】分别写出两个命题的逆命题,根据平行线的性质、角的定义判断即可.
本题考查的是命题的真假判断、逆命题的概念,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.
16.【答案】解:上述问题有三种正确命题,分别是:
命题1:;命题2:;命题3:.
解:选择命题2:.
证明:,,.
平分,.
.
【解析】根据题意,结合平行线的性质,选择两个条件做题设,一个条件做结论,得到正确的命题;任选一个命题,根据平行线的性质或角平分线的定义进行证明.
本题考查的是平行线的性质以及角平分线的性质,本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.
17.【答案】解:三角形两条边上的中垂线的交点到各顶点的距离相等;真命题;理由如下:
如图,
是线段AB和线段AC的垂直平分线的交点,
,,
,
三角形两条边上的中垂线的交点到各顶点的距离相等;
有公共顶点且相等的两个角是对顶角;假命题;理由如下:
两条直线相交所形成的角中相对的角是对顶角,
例如,平角的角平分线把平角分为两个直角,这两个直角不是对顶角,
是假命题.
【解析】由线段垂直平分线的性质即可得出结论;
由对顶角定义进行判断即可.
本题考查的是命题的证明,熟练掌握线段垂直平分线的性质、对顶角定义是解题的关键.
18.【答案】解:一个三角形如果有两个内角互余,那么这个三角形是直角三角形,此命题为真命题;
当,,则,所以命题“如果,那么”为假命题;
同角的补角相等,此命题为真命题;
两无理数为和,它们的和为0,命题“两个无理数的和仍是无理数”为假命题.
【解析】利用三角形内角和和互余的定义对进行判断;
利用反例进行判断;
根据补角的定义进行判断;
利用反例进行判断.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
第2页,共2页
第1页,共1页
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
