29.2 三视图(第二课时 由三视图确定几何体及几何体面积)同步练习(含解析)
文档属性
| 名称 | 29.2 三视图(第二课时 由三视图确定几何体及几何体面积)同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 10:48:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
29.2 三视图(第二课时 由三视图确定几何体及几何体面积)练习
一、单选题(共10小题)
1.(2018·罗平县旧屋基民族中学九年级期末)由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )
A.3块 B.4块 C.6块 D.9块
2.(2020·山东枣庄市·九年级期中)某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.4个 B.5个 C.6个 D.7个
3.(2020·山东枣庄市·九年级期末)用小立方块搭成的几何体,从正面看和从上面看的形状图如下,则组成这样的几何体需要的立方块个数为( )
A.最多需要8块,最少需要6块 B.最多需要9块,最少需要6块
C.最多需要8块,最少需要7块 D.最多需要9块,最少需要7块
4.(2020·黑龙江大庆市·九年级期末)一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )
A. B. C. D.
5.(2020·新疆期末)“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )
A.68π cm2 B.74π cm2 C.84π cm2 D.100π cm2
6.(2020·新疆期末)一个几何体的三视图如图所示,那么这个几何体的侧面积是( )
A. B. C. D.
7.(2018·河北唐山市·七年级期末)将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )
A.3 B.9 C.12 D.18
8.(2017·山东烟台市·九年级期末)如图是某工件的三视图,则此工件的表面积为( )
A.15πcm2 B.51πcm2 C.66πcm2 D.24πcm2
9.(2018·湖南期末)如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
A.200 cm2 B.600 cm2 C.100πcm2 D.200πcm2
10.(2018·深圳市·九年级期末)一个几何体有n个大小相同的小正方形搭成,其左视图、俯视图、如图所示,则n的值最小是( )
A.5 B.7 C.9 D.10
二、填空题(共5小题)
11.(2018·江苏无锡市·七年级期末)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为_____.
12.(2020·山东济宁市·九年级期末)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为___________.
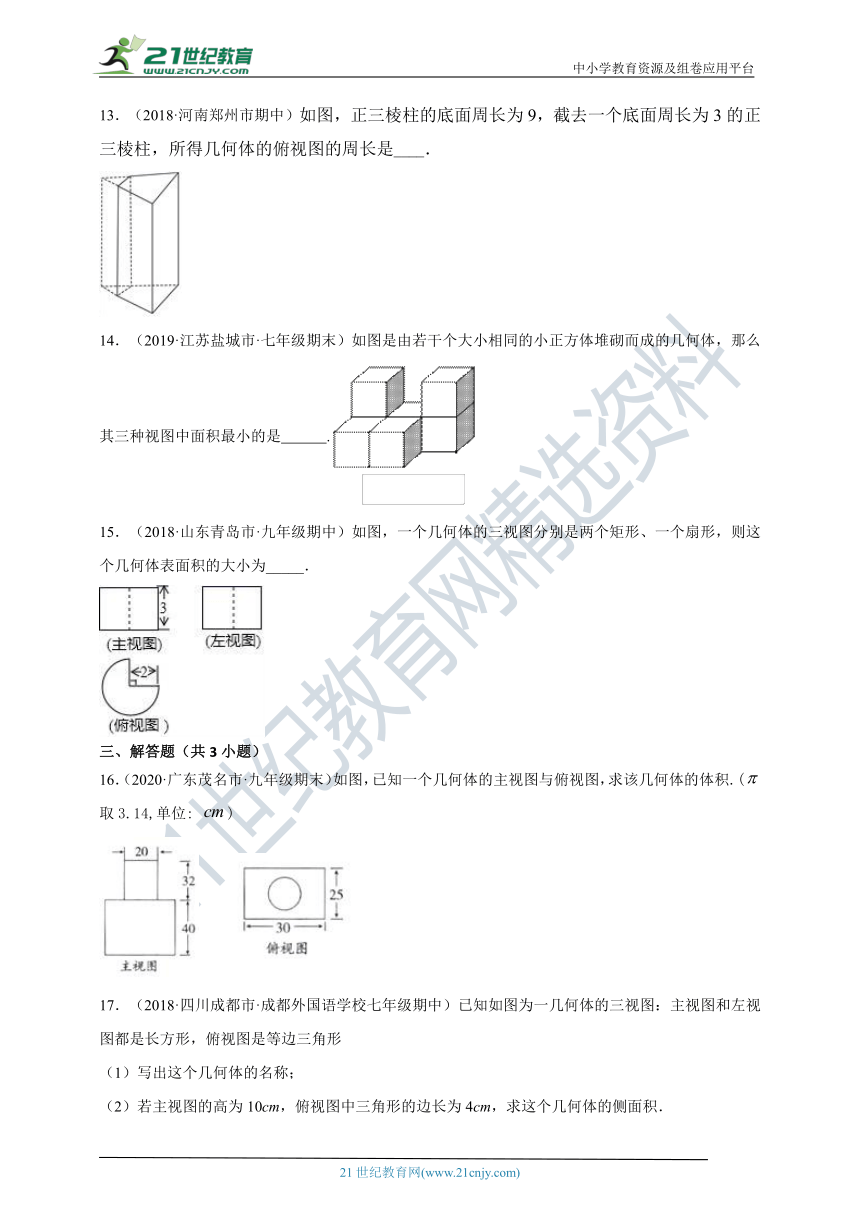
13.(2018·河南郑州市期中)如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是____.
14.(2019·江苏盐城市·七年级期末)如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 .
15.(2018·山东青岛市·九年级期中)如图,一个几何体的三视图分别是两个矩形、一个扇形,则这个几何体表面积的大小为_____.
三、解答题(共3小题)
16.(2020·广东茂名市·九年级期末)如图,已知一个几何体的主视图与俯视图,求该几何体的体积.(取3.14,单位: )
17.(2018·四川成都市·成都外国语学校七年级期中)已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
18.(2020·江西吉安市·九年级期末)一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.
答案
一、单选题(共10小题)
1.B
解答:解:从俯视图可得最底层有3个小正方体,由主视图可得有2层上面一层是1个小正方体,下面有2个小正方体,从左视图上看,后面一层是2个小正方体,前面有1个小正方体,所以此几何体共有四个正方体.
故选B.
2.B
【详解】由主视图和左视图可确定所需正方体个数最少时俯视图(数字为该位置小正方体的个数)为:
则搭成这个几何体的小正方体最少有5个,
故选B.
3.C
【详解】
由主视图可得:这个几何体共有3层,
由俯视图可知第一层正方体的个数为4,
由主视图可知第二层最少为2块,最多的正方体的个数为3块,
第三层只有一块,
故:最多为3+4+1=8个
最少为2+4+1=7个
故选C
4.B
【详解】
解:由三视图可知圆柱的底面直径为,高为,
底面半径为,
,
故选B.
5.C
【解析】
试题分析:∵底面圆的直径为8cm,高为3cm,∴母线长为5cm,∴其表面积=π×4×5+42π+8π×6=84πcm2,故选C.
考点:圆锥的计算;几何体的表面积.
6.B
【详解】
∵一个圆柱的底面直径为2,高为3,
∴这个圆柱的侧面积是:πd×3=6π.
故选:B.
7.D
【解析】
试题分析:观察几何体,得到这个几何体向前、向后、向上、向下、向左、向右分别有3个正方形,则它的表面积=6×3×1=18.
故选D.
8.D
【详解】
解:观察几何体的三视图可得该几何体为圆锥,如图所示,OB=3cm,OA=4cm,
由勾股定理求得AB=5cm,
所以圆锥的侧面积为×6π×5=15πcm2,
圆锥的底面积为π×()2=9πcm,
即可得圆锥的表面积15π+9π=24πcm2,
故答案选D.
9.D
【解析】
试题解析:由三视图可知,该几何体为圆柱,由俯视图可得底面周长为 cm,由主视图可得圆柱的高为20 cm,所以圆柱的侧面积为 .
所以本题应选D.
10.B
【详解】
由题中所给出的左视图知物体共三层,每一层都是两个小正方体;
从俯视图可以可以看出最底层的个数,所以图中的小正方体最少1+2+4=7.
故选B.
二、填空题(共5小题)
11.108
【详解】
观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,
故答案为:108.
12.cm2
【解析】
根据三视图得到圆锥的底面圆的直径为6cm,即底面圆的半径为3cm,圆锥的高为4cm,
所以圆锥的母线长= =5,所以这个圆锥的侧面积=π×3×5=15π(cm2).
故答案为15πcm2.
13.8
【解析】
试题分析:根据从上边看得到的图形是俯视图,可知从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为8.
14.左视图
【详解】
解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为左视图
15.12+15π
【解析】
试题分析:由几何体的三视图可得:该几何体是长方体、两个扇形和一个矩形的组合体,该组合体的表面积为:S=2×2×3+×2+×3=12+15π,故答案为12+15π.
三、解答题(共3小题)
16.40048
【详解】
解:由几何体的主视图和俯视图,可以想象出该几何体由两部分组成:上部是一个圆柱,底面直径是20cm,高是32cm;下部是一个长方体,长、宽、高分别是30cm,25cm,40cm,所以该几何体的体积为.
17.(1)三棱柱;(2)这个几何体的侧面面积为120cm2.
【详解】
解:(1)这个几何体是三棱柱;
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长即:
C=4×3=12cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为:
S=12×10=120cm2.
答:这个几何体的侧面面积为120cm2.
故答案为(1)三棱柱;(2)120cm2.
18.
试题解析:
∵俯视图是菱形,
∴可求得底面菱形边长为2.5,
上、下底面积和为6×2=12,
侧面积为2.5×4×8=80
∴直棱柱的表面积为
_21?????????è?????(www.21cnjy.com)_
29.2 三视图(第二课时 由三视图确定几何体及几何体面积)练习
一、单选题(共10小题)
1.(2018·罗平县旧屋基民族中学九年级期末)由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )
A.3块 B.4块 C.6块 D.9块
2.(2020·山东枣庄市·九年级期中)某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.4个 B.5个 C.6个 D.7个
3.(2020·山东枣庄市·九年级期末)用小立方块搭成的几何体,从正面看和从上面看的形状图如下,则组成这样的几何体需要的立方块个数为( )
A.最多需要8块,最少需要6块 B.最多需要9块,最少需要6块
C.最多需要8块,最少需要7块 D.最多需要9块,最少需要7块
4.(2020·黑龙江大庆市·九年级期末)一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为( )
A. B. C. D.
5.(2020·新疆期末)“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )
A.68π cm2 B.74π cm2 C.84π cm2 D.100π cm2
6.(2020·新疆期末)一个几何体的三视图如图所示,那么这个几何体的侧面积是( )
A. B. C. D.
7.(2018·河北唐山市·七年级期末)将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )
A.3 B.9 C.12 D.18
8.(2017·山东烟台市·九年级期末)如图是某工件的三视图,则此工件的表面积为( )
A.15πcm2 B.51πcm2 C.66πcm2 D.24πcm2
9.(2018·湖南期末)如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
A.200 cm2 B.600 cm2 C.100πcm2 D.200πcm2
10.(2018·深圳市·九年级期末)一个几何体有n个大小相同的小正方形搭成,其左视图、俯视图、如图所示,则n的值最小是( )
A.5 B.7 C.9 D.10
二、填空题(共5小题)
11.(2018·江苏无锡市·七年级期末)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为_____.
12.(2020·山东济宁市·九年级期末)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为___________.
13.(2018·河南郑州市期中)如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是____.
14.(2019·江苏盐城市·七年级期末)如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 .
15.(2018·山东青岛市·九年级期中)如图,一个几何体的三视图分别是两个矩形、一个扇形,则这个几何体表面积的大小为_____.
三、解答题(共3小题)
16.(2020·广东茂名市·九年级期末)如图,已知一个几何体的主视图与俯视图,求该几何体的体积.(取3.14,单位: )
17.(2018·四川成都市·成都外国语学校七年级期中)已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
18.(2020·江西吉安市·九年级期末)一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.
答案
一、单选题(共10小题)
1.B
解答:解:从俯视图可得最底层有3个小正方体,由主视图可得有2层上面一层是1个小正方体,下面有2个小正方体,从左视图上看,后面一层是2个小正方体,前面有1个小正方体,所以此几何体共有四个正方体.
故选B.
2.B
【详解】由主视图和左视图可确定所需正方体个数最少时俯视图(数字为该位置小正方体的个数)为:
则搭成这个几何体的小正方体最少有5个,
故选B.
3.C
【详解】
由主视图可得:这个几何体共有3层,
由俯视图可知第一层正方体的个数为4,
由主视图可知第二层最少为2块,最多的正方体的个数为3块,
第三层只有一块,
故:最多为3+4+1=8个
最少为2+4+1=7个
故选C
4.B
【详解】
解:由三视图可知圆柱的底面直径为,高为,
底面半径为,
,
故选B.
5.C
【解析】
试题分析:∵底面圆的直径为8cm,高为3cm,∴母线长为5cm,∴其表面积=π×4×5+42π+8π×6=84πcm2,故选C.
考点:圆锥的计算;几何体的表面积.
6.B
【详解】
∵一个圆柱的底面直径为2,高为3,
∴这个圆柱的侧面积是:πd×3=6π.
故选:B.
7.D
【解析】
试题分析:观察几何体,得到这个几何体向前、向后、向上、向下、向左、向右分别有3个正方形,则它的表面积=6×3×1=18.
故选D.
8.D
【详解】
解:观察几何体的三视图可得该几何体为圆锥,如图所示,OB=3cm,OA=4cm,
由勾股定理求得AB=5cm,
所以圆锥的侧面积为×6π×5=15πcm2,
圆锥的底面积为π×()2=9πcm,
即可得圆锥的表面积15π+9π=24πcm2,
故答案选D.
9.D
【解析】
试题解析:由三视图可知,该几何体为圆柱,由俯视图可得底面周长为 cm,由主视图可得圆柱的高为20 cm,所以圆柱的侧面积为 .
所以本题应选D.
10.B
【详解】
由题中所给出的左视图知物体共三层,每一层都是两个小正方体;
从俯视图可以可以看出最底层的个数,所以图中的小正方体最少1+2+4=7.
故选B.
二、填空题(共5小题)
11.108
【详解】
观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,
故答案为:108.
12.cm2
【解析】
根据三视图得到圆锥的底面圆的直径为6cm,即底面圆的半径为3cm,圆锥的高为4cm,
所以圆锥的母线长= =5,所以这个圆锥的侧面积=π×3×5=15π(cm2).
故答案为15πcm2.
13.8
【解析】
试题分析:根据从上边看得到的图形是俯视图,可知从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为8.
14.左视图
【详解】
解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为左视图
15.12+15π
【解析】
试题分析:由几何体的三视图可得:该几何体是长方体、两个扇形和一个矩形的组合体,该组合体的表面积为:S=2×2×3+×2+×3=12+15π,故答案为12+15π.
三、解答题(共3小题)
16.40048
【详解】
解:由几何体的主视图和俯视图,可以想象出该几何体由两部分组成:上部是一个圆柱,底面直径是20cm,高是32cm;下部是一个长方体,长、宽、高分别是30cm,25cm,40cm,所以该几何体的体积为.
17.(1)三棱柱;(2)这个几何体的侧面面积为120cm2.
【详解】
解:(1)这个几何体是三棱柱;
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长即:
C=4×3=12cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为:
S=12×10=120cm2.
答:这个几何体的侧面面积为120cm2.
故答案为(1)三棱柱;(2)120cm2.
18.
试题解析:
∵俯视图是菱形,
∴可求得底面菱形边长为2.5,
上、下底面积和为6×2=12,
侧面积为2.5×4×8=80
∴直棱柱的表面积为
_21?????????è?????(www.21cnjy.com)_
