第二十九章 投影与视图单元测试卷(含解析)
文档属性
| 名称 | 第二十九章 投影与视图单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 14:19:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十九章 投影与视图
(满分:100分 时间:90分钟)
班级_________ 姓名_________ 学号_________ 分数_________
一、单选题(共10小题,每小题3分,共计30分)
1.(2020·甘肃张掖市·九年级期中)下面四幅图是在同一天同一地点不同时刻太阳照射同一根旗杆的影像图,其中表示太阳刚升起时的影像图是( )
A. B.
C. D.
2.(2019·河南郑州市期中)如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
A.(1)(2)(3)(4) B.(4)(3)(2)(1) C.(4)(3)(1)(2) D.(2)(3)(4)(1)
3.(2019·平顶山市期中)小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.上午8时 B.上午9时30分 C.上午10时 D.上午12时
4.(2018·广东深圳市·九年级期末)如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为1:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )
A.8cm B.20cm C.3.2cm D.10cm
5.(2018·山东烟台市·九年级期末)下列说法正确的是( )
A.三角形的正投影一定是三角形 B.长方体的正投影一定是长方形
C.球的正投影一定是圆 D.圆锥的正投影一定是三角形
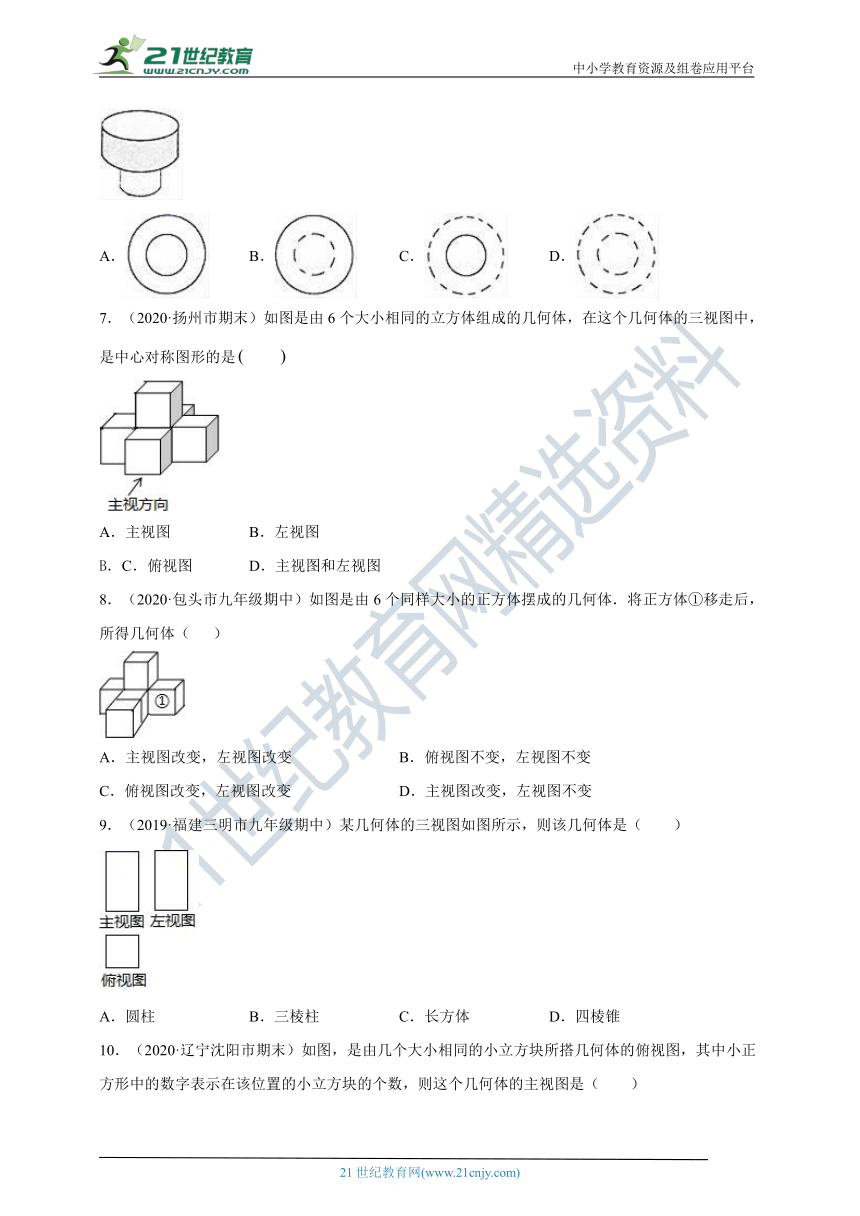
6.(2020·广东深圳市九年级期末)如图所示的工件,其俯视图是( )
A. B. C. D.
7.(2020·扬州市期末)如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是
主视图 B.左视图
C.俯视图 D.主视图和左视图
8.(2020·包头市九年级期中)如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变 B.俯视图不变,左视图不变
C.俯视图改变,左视图改变 D.主视图改变,左视图不变
9.(2019·福建三明市九年级期中)某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.三棱柱 C.长方体 D.四棱锥
10.(2020·辽宁沈阳市期末)如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
A. B. C. D.
二、填空题(共5小题,每小题4分,共计20分)
11.(2019·辽宁朝阳市·九年级期末)如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)________.①越来越长,②越来越短,③长度不变.
在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是________米.
12.(2019·北京市九年级期中)如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为_____米.
13.(2018·江苏无锡市期末)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为_____.
14.(2020·山东济宁市期末)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为___________.
15.(2018·内蒙古赤峰市·七年级期末)用小正方体搭一几何体,从正面和上面看如图所示,这个几何体最少要_______个正方体,最多要_______个正方体.
正面 上面
解答题(共5小题,每小题10分,共计50分)
16.(2020·银川市九年级期末)李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
17.(2020·渠县九年级期末)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
18.(2019·江苏南京市七年级期末)如图是由10个同样大小的小正方体搭成的物体,
(1)请分别画出它的主视图和俯视图.
(2)在主视图和俯视图不变的情况下,你认为最多还可以添加 个小正方体.
19.(2019·惠来县七年级期中)一个几何体是由若干个棱长为3cm的小正方体搭成的,从正面、左面、上面看到的几何体的形状图如图所示:
(1)在“从上面看”的图中标出各个位置上小正方体的个数;
(2)求该几何体的体积.
20.(2020·河南南阳市期末)由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
答案
一、单选题(共10小题,每小题3分,共计30分)
1.C
解:太阳东升西落,在不同的时刻,
同一物体的影子的方向和大小不同,太阳从东方刚升起时,影子应在西方.
故选C.
2.C
【详解】
根据平行投影的规律知:顺序为(4)(3)(1)(2).
故选B.
3.A
【详解】
解:根据从早晨到傍晚影子的指向是:西-西北-北-东北-东,影长由长变短,再变长.
可知影子最长的时刻为上午8时.
故选A.
4.D
【详解】
∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为1:2,三角尺的一边长为5cm,∴投影三角形的对应边长为:510(cm).
故选D.
5.C
【详解】
A. 三角形的正投影不一定是三角形,错误
B. 长方体的正投影不一定是长方形,错误
C. 球的正投影一定是圆,正确
D. 圆锥的正投影不一定是三角形,错误
故选C.
6.B
【解析】
试题分析:从上边看是一个同心圆,外圆是实线,內圆是虚线,
故选B.
7.C
【详解】观察几何体,可得三视图如图所示:
可知俯视图是中心对称图形,
故选C.
8.D
试题分析:将正方体①移走前的主视图正方形的个数为1,2,1;正方体①移走后的主视图正方形的个数为1,2;发生改变.将正方体①移走前的左视图正方形的个数为2,1,1;正方体①移走后的左视图正方形的个数为2,1,1;没有发生改变.将正方体①移走前的俯视图正方形的个数为1,3,1;正方体①移走后的俯视图正方形的个数,1,3;发生改变.故选D.
9.C
【详解】
A、圆柱的主视图和左视图是矩形,但俯视图是圆,不符合题意;
B、三棱柱的主视图和左视图是矩形,但俯视图是三角形,不符合题意;
C、长方体的主视图、左视图及俯视图都是矩形,符合题意;
D、四棱锥的主视图、左视图都是三角形,而俯视图是四边形,不符合题意;
故选C.
10.C
【详解】
由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2列只有前排2个正方形,
所以其主视图为:
故选C.
二、填空题(共5小题,每小题4分,共计20分)
11.①;5.95.
【解析】
试题解析:小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会越来越长;
∵CD∥AB,
∴△ECD∽△EBA,
∴,即,
∴AB=5.95(m).
12.6.4
【详解】
解:由题可知:,
解得:树高=6.4米.
13.108
【详解】
观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,
故答案为:108.
14.cm2
【解析】
根据三视图得到圆锥的底面圆的直径为6cm,即底面圆的半径为3cm,圆锥的高为4cm,
所以圆锥的母线长= =5,所以这个圆锥的侧面积=π×3×5=15π(cm2).
故答案为15πcm2.
15.10 14
【解析】
试题解析:搭这样的几何体最少需要7+2+1=10个小正方体,
最多需要7+4+3=14个小正方体;
故最多需要14个小正方体,最少需要10个小正方体.
故答案为:10,14;
解答题(共5小题,每小题10分,共计50分)
16.21.2m
【详解】
解:作DN⊥AB.垂足为N,交EF于M,
∴四边形CDME、ACDN是矩形,
∴AN=ME=CD=1.2m,DN=AC=30m,DM=CE=0.6m,
∴MF=EF-ME=1.6-1.2=0.4m,
∴依题意知,EF∥AB,
∴△DFM∽△DBN,
∴,
即: ,
∴BN=20,
∴AB=BN+AN=20+1.2=21.2
答:楼高为21.2米.
17.(1)画图见解析;(2)DE=4.
【详解】
(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,,
∴,
∴OD=4m,
∴灯泡的高为4m.
18.(1)作图见解析;(2)最多还可以添加3个小正方体.
【详解】
(1)如图所示:
;
(2)在上面两个平面图形不变的情况下,如图所示,可知最多还可以添加 3个小正方体,
故答案为3.
19.(1)见解析;(2)270cm3
【详解】
(1)如图所示:
(2)该几何体的体积为33×(2+3+2+1+1+1)=27×10=270(cm3).
20.(1)见解析(2)24(3)26
【详解】
主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1,
图形分别如下:
由题意可得:上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,
故可得表面积为:.
要使表面积最大,则需满足两正方体重合的最少,此时俯视图为:
这样上面共有3个小正方形,下面共有3个小正方形;左面共有5个小正方形,右面共有5个正方形;前面共有5个小正方形,后面共有5个正方形,
表面积为:.
故答案为24、26.
_21?????????è?????(www.21cnjy.com)_
第二十九章 投影与视图
(满分:100分 时间:90分钟)
班级_________ 姓名_________ 学号_________ 分数_________
一、单选题(共10小题,每小题3分,共计30分)
1.(2020·甘肃张掖市·九年级期中)下面四幅图是在同一天同一地点不同时刻太阳照射同一根旗杆的影像图,其中表示太阳刚升起时的影像图是( )
A. B.
C. D.
2.(2019·河南郑州市期中)如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
A.(1)(2)(3)(4) B.(4)(3)(2)(1) C.(4)(3)(1)(2) D.(2)(3)(4)(1)
3.(2019·平顶山市期中)小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.上午8时 B.上午9时30分 C.上午10时 D.上午12时
4.(2018·广东深圳市·九年级期末)如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为1:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )
A.8cm B.20cm C.3.2cm D.10cm
5.(2018·山东烟台市·九年级期末)下列说法正确的是( )
A.三角形的正投影一定是三角形 B.长方体的正投影一定是长方形
C.球的正投影一定是圆 D.圆锥的正投影一定是三角形
6.(2020·广东深圳市九年级期末)如图所示的工件,其俯视图是( )
A. B. C. D.
7.(2020·扬州市期末)如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是
主视图 B.左视图
C.俯视图 D.主视图和左视图
8.(2020·包头市九年级期中)如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变 B.俯视图不变,左视图不变
C.俯视图改变,左视图改变 D.主视图改变,左视图不变
9.(2019·福建三明市九年级期中)某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.三棱柱 C.长方体 D.四棱锥
10.(2020·辽宁沈阳市期末)如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
A. B. C. D.
二、填空题(共5小题,每小题4分,共计20分)
11.(2019·辽宁朝阳市·九年级期末)如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)________.①越来越长,②越来越短,③长度不变.
在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是________米.
12.(2019·北京市九年级期中)如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为_____米.
13.(2018·江苏无锡市期末)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为_____.
14.(2020·山东济宁市期末)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为___________.
15.(2018·内蒙古赤峰市·七年级期末)用小正方体搭一几何体,从正面和上面看如图所示,这个几何体最少要_______个正方体,最多要_______个正方体.
正面 上面
解答题(共5小题,每小题10分,共计50分)
16.(2020·银川市九年级期末)李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
17.(2020·渠县九年级期末)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
18.(2019·江苏南京市七年级期末)如图是由10个同样大小的小正方体搭成的物体,
(1)请分别画出它的主视图和俯视图.
(2)在主视图和俯视图不变的情况下,你认为最多还可以添加 个小正方体.
19.(2019·惠来县七年级期中)一个几何体是由若干个棱长为3cm的小正方体搭成的,从正面、左面、上面看到的几何体的形状图如图所示:
(1)在“从上面看”的图中标出各个位置上小正方体的个数;
(2)求该几何体的体积.
20.(2020·河南南阳市期末)由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
答案
一、单选题(共10小题,每小题3分,共计30分)
1.C
解:太阳东升西落,在不同的时刻,
同一物体的影子的方向和大小不同,太阳从东方刚升起时,影子应在西方.
故选C.
2.C
【详解】
根据平行投影的规律知:顺序为(4)(3)(1)(2).
故选B.
3.A
【详解】
解:根据从早晨到傍晚影子的指向是:西-西北-北-东北-东,影长由长变短,再变长.
可知影子最长的时刻为上午8时.
故选A.
4.D
【详解】
∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为1:2,三角尺的一边长为5cm,∴投影三角形的对应边长为:510(cm).
故选D.
5.C
【详解】
A. 三角形的正投影不一定是三角形,错误
B. 长方体的正投影不一定是长方形,错误
C. 球的正投影一定是圆,正确
D. 圆锥的正投影不一定是三角形,错误
故选C.
6.B
【解析】
试题分析:从上边看是一个同心圆,外圆是实线,內圆是虚线,
故选B.
7.C
【详解】观察几何体,可得三视图如图所示:
可知俯视图是中心对称图形,
故选C.
8.D
试题分析:将正方体①移走前的主视图正方形的个数为1,2,1;正方体①移走后的主视图正方形的个数为1,2;发生改变.将正方体①移走前的左视图正方形的个数为2,1,1;正方体①移走后的左视图正方形的个数为2,1,1;没有发生改变.将正方体①移走前的俯视图正方形的个数为1,3,1;正方体①移走后的俯视图正方形的个数,1,3;发生改变.故选D.
9.C
【详解】
A、圆柱的主视图和左视图是矩形,但俯视图是圆,不符合题意;
B、三棱柱的主视图和左视图是矩形,但俯视图是三角形,不符合题意;
C、长方体的主视图、左视图及俯视图都是矩形,符合题意;
D、四棱锥的主视图、左视图都是三角形,而俯视图是四边形,不符合题意;
故选C.
10.C
【详解】
由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2列只有前排2个正方形,
所以其主视图为:
故选C.
二、填空题(共5小题,每小题4分,共计20分)
11.①;5.95.
【解析】
试题解析:小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会越来越长;
∵CD∥AB,
∴△ECD∽△EBA,
∴,即,
∴AB=5.95(m).
12.6.4
【详解】
解:由题可知:,
解得:树高=6.4米.
13.108
【详解】
观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,
故答案为:108.
14.cm2
【解析】
根据三视图得到圆锥的底面圆的直径为6cm,即底面圆的半径为3cm,圆锥的高为4cm,
所以圆锥的母线长= =5,所以这个圆锥的侧面积=π×3×5=15π(cm2).
故答案为15πcm2.
15.10 14
【解析】
试题解析:搭这样的几何体最少需要7+2+1=10个小正方体,
最多需要7+4+3=14个小正方体;
故最多需要14个小正方体,最少需要10个小正方体.
故答案为:10,14;
解答题(共5小题,每小题10分,共计50分)
16.21.2m
【详解】
解:作DN⊥AB.垂足为N,交EF于M,
∴四边形CDME、ACDN是矩形,
∴AN=ME=CD=1.2m,DN=AC=30m,DM=CE=0.6m,
∴MF=EF-ME=1.6-1.2=0.4m,
∴依题意知,EF∥AB,
∴△DFM∽△DBN,
∴,
即: ,
∴BN=20,
∴AB=BN+AN=20+1.2=21.2
答:楼高为21.2米.
17.(1)画图见解析;(2)DE=4.
【详解】
(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,,
∴,
∴OD=4m,
∴灯泡的高为4m.
18.(1)作图见解析;(2)最多还可以添加3个小正方体.
【详解】
(1)如图所示:
;
(2)在上面两个平面图形不变的情况下,如图所示,可知最多还可以添加 3个小正方体,
故答案为3.
19.(1)见解析;(2)270cm3
【详解】
(1)如图所示:
(2)该几何体的体积为33×(2+3+2+1+1+1)=27×10=270(cm3).
20.(1)见解析(2)24(3)26
【详解】
主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1,
图形分别如下:
由题意可得:上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,
故可得表面积为:.
要使表面积最大,则需满足两正方体重合的最少,此时俯视图为:
这样上面共有3个小正方形,下面共有3个小正方形;左面共有5个小正方形,右面共有5个正方形;前面共有5个小正方形,后面共有5个正方形,
表面积为:.
故答案为24、26.
_21?????????è?????(www.21cnjy.com)_
