7.1 探索直线平行的条件(第1课时)(共28张PPT)
文档属性
| 名称 | 7.1 探索直线平行的条件(第1课时)(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 19:25:24 | ||
图片预览




文档简介
7.1 探索直线平行的条件
第7章 平面图形的认识(二)
第1课时
2020-2021学年度苏科版七年级下册
判断:
1.同一平面内,直线有平行和垂直两种位置关系
2.与一条直线平行的直线只有一条.
3.两条直线不相交,就叫做平行线.
(×)
(×)
(×)
复习旧知
如图,装修工人正在向墙上钉木条,如果木条b与墙壁的边缘垂直,那么木条a与墙壁的边缘所夹的角为多少度时,才能使木条a与木条b平行?
答: 木条 a 与墙壁的边缘也垂直时才能使木条a与木条b平行.
平行在日常生活中的应用
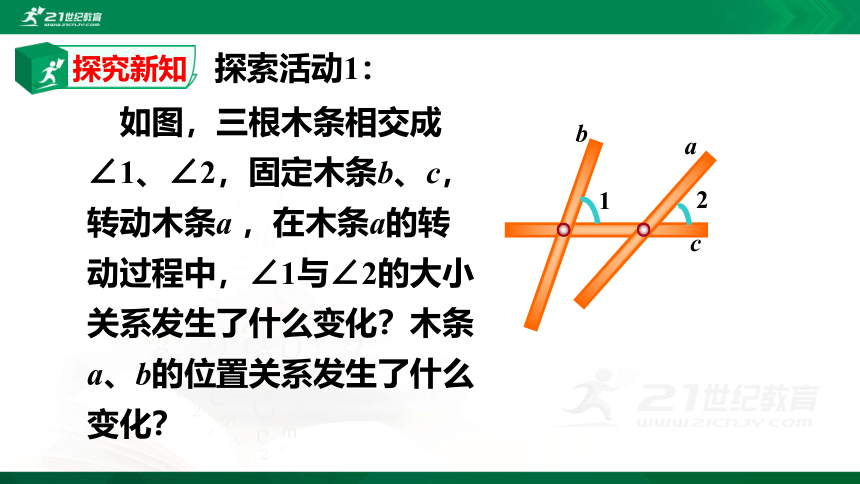
如图,三根木条相交成∠1、∠2,固定木条b、c,转动木条a ,在木条a的转动过程中,∠1与∠2的大小关系发生了什么变化?木条a、b的位置关系发生了什么变化?
探索活动1:
1
2
b
a
c
探究新知
1
2
b
a
c
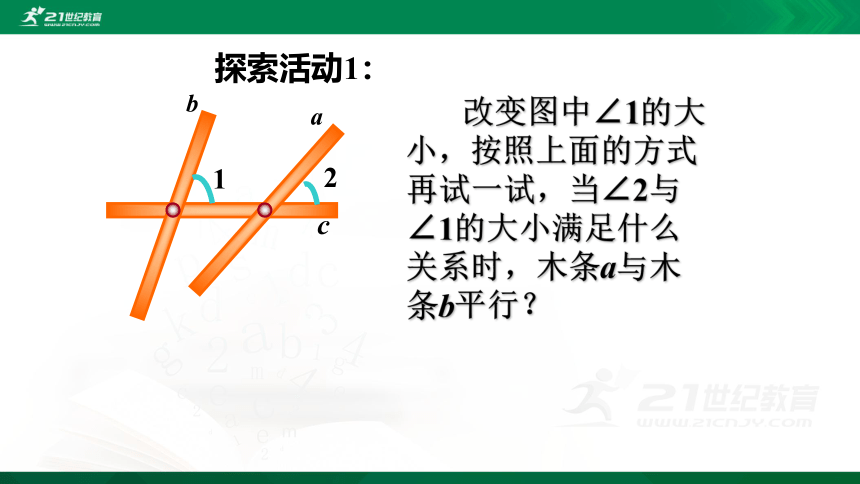
改变图中∠1的大小,按照上面的方式再试一试,当∠2与∠1的大小满足什么关系时,木条a与木条b平行?
探索活动1:
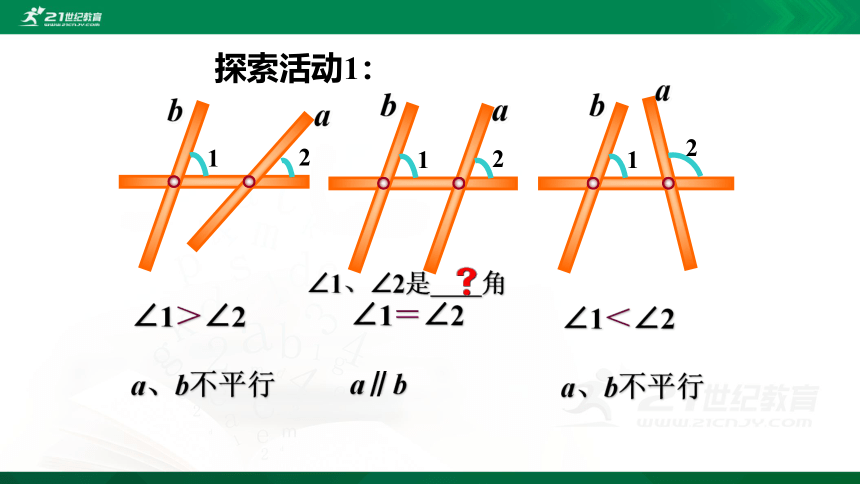
∠1>∠2
a、b不平行
∠1=∠2
a∥b
∠1<∠2
a、b不平行
1
2
1
2
1
2
b
a
b
b
a
a
∠1、∠2是 角
探索活动1:
3
4
5
6
7
8
1
2
a
b
c
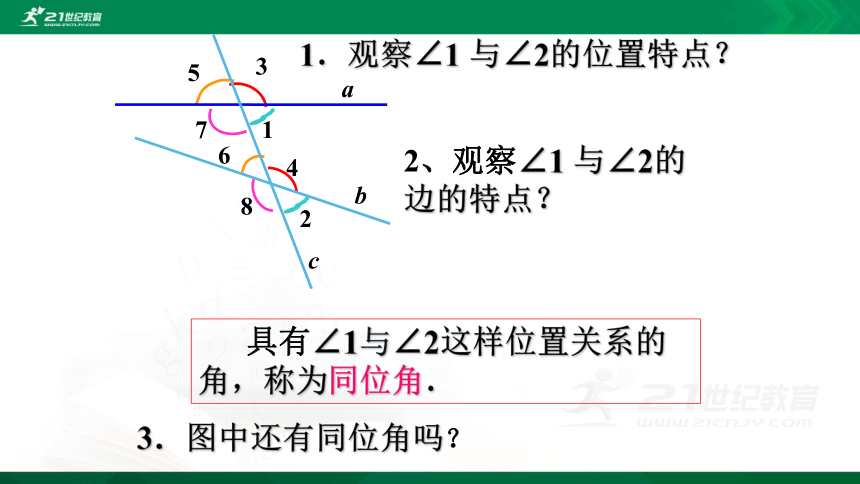
1.观察∠1 与∠2的位置特点?
具有∠1与∠2这样位置关系的角,称为同位角.
3.图中还有同位角吗?
2、观察∠1 与∠2的边的特点?
我们把具有∠1与∠2这样位置关系的角称为同位角.
两直线AB、CD被第三直线EF所截,构成了八个角.
同 位 角 的 定 义
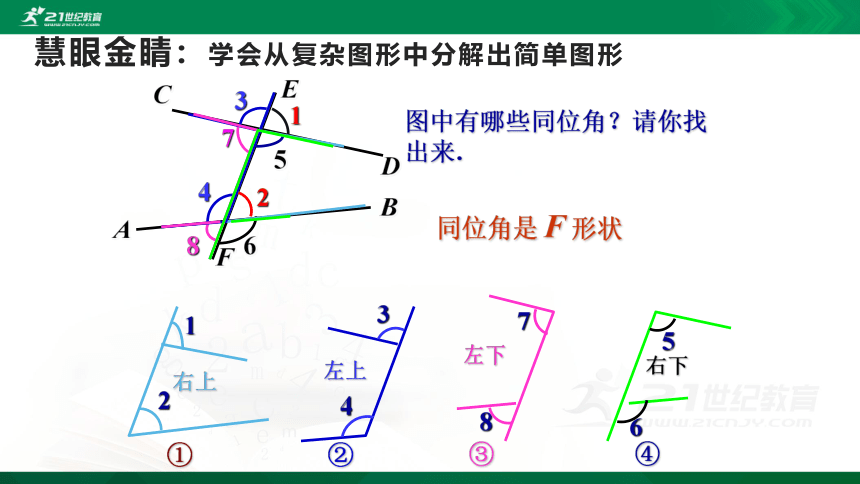
慧眼金睛:学会从复杂图形中分解出简单图形
图中有哪些同位角?请你找出来.
F
1
3
7
5
2
4
8
6
D
C
A
B
E
①
②
③
④
2
1
4
3
7
6
5
8
右上
左上
左下
右下
同位角是 F 形状
判断两条直线平行的方法:
由此可得:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线互相平行.
F
1
2
3
4
5
6
7
8
D
C
A
B
E
探索活动
你能找到一对同位角吗?
★ 在判别“同位角”时,要注意“两同”:在第三条直线的同旁;在被截两条直线的同一方向.
解:在图7-5中,AB∥CD,AC∥BD.
因为∠1与∠C是AB、CD被AC截成的同位角,且∠1=∠C,
所以AB∥CD.
理由是:同位角相等,两直线平行.
因为∠2与∠C是BD、AC被CD截成的同位角,且∠2=∠C,
所以AC//BD.
理由是:同位角相等,两直线平行.
例1 如图7-5,∠1=∠C,∠2=∠C.指出图中互相平行的直线,并说明理由.
典例讲解
知识加油站
1. 图中∠3与∠5,∠4与∠6这样位置关系的角有什么特点?说说你的理由.
2. ∠3与∠6,∠4与∠5这样位置关系的角呢?说说你的理由.
a
b
c
1
2
3
4
5
6
7
8
∠3与∠5,∠4与∠6这样位置关系的角,在两条被截直线的内部,在截线的两侧,位置是交错的,
这样的角叫做内错角.
∠3与∠6,∠4与∠5这样位置关系的角,在两条被截直线的内部,在截线的同旁,这样的角叫做同旁内角.
1. 观察右图并填空:
(1)∠1 与 是同位角;
(2)∠5 与 是同旁内角;
(3)∠1 与 是内错角.
∠4
∠3
∠2
b
a
n
m
2
3
1
4
5
针对练习
4
1
2
3
5
6
7
8
D
C
B
E
A
F
2. 如图,直线AB,CD被EF所截,构成了八个角,你能找出哪些角是同位角、内错角、同旁内角吗?
议一议
探索直线平行的条件
(一)内错角满足什么关系时?两直线平行?
(二)同旁内角满足什么关系时?两直线平行?
内错角相等,两直线平行.
同旁内角互补,两直线平行.
为什么?
为什么?
做一做:你能用三块大小相同的三角板(30°,60°,90°)拼接成一个含有平行线段的图形吗?试一试,多拼几个图形,找出平行线段后,说明你的理由.
1.图中各角分别满足下列条件时,你能判断哪两条直线平行吗?
①∠1=∠4 ②∠2=∠4 ③∠1+∠3=180°
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
针对练习
例2 如图7-9, ∠ 1=∠2,∠B+ ∠ BDE=180 °.指出图中互相平行的直线,并说明理由.
因为∠ B与∠ BDE是BC、DE被AB截成的同旁内角,且∠ B+∠ BDE=180°,
所以DE ∥BC.
理由是:同旁内角互补,两直线平行.
解:在图7-9中,AB ∥ EF,DE ∥ BC.
因为∠1与∠2是AB、EF被DE截成的内错角,
且∠1=∠2,
所以AB ∥ EF.
理由是:内错角相等,两直线平行.
典例讲解
例、如图,∠1=∠2=55°,∠3等于多少度?直线AB、CD平行吗?说明你的理由.
第2题图
3
1
2
A
B
F
C
D
E
∵∠2=55°
∴∠3=∠2=55°
∴∠3=∠1=55°
∴AB∥CD.
( )
对顶角相等
解: AB∥CD. 理由如下:
(已知)
(等量代换)
(同位角相等,两直线平行)
∵∠1= 55°
(已知)
1.找出下面点阵 (点阵中相邻的四个点构成正方形) 中互相平行的线段.
① AB∥CD
② EF∥GH
∵ ∠AMP=∠CPF
∵ ∠AMP=∠ANQ
E
G
B
D
F
H
A
C
M
N
P
Q
同位角相等,两直线平行.
同位角相等,两直线平行.
2.如图,∠1=∠2,直线AB,CD平行吗?
A
B
C
D
2
1
3
∵∠1=55°;
对顶角相等.
∴∠3=55°;
∵∠3 =∠2=55°;
∴ AB∥CD.
1.观察右图并填空:
∠1与 是同位角;
∠5与 是同旁内角;
(3) ∠2与 是内错角.
∠4
∠3
∠1
2.当图中各角分别满足下列条件时,你能支出哪两条直线平行吗?
∠1=∠4;
(2) ∠2=∠4;
(3)∠1+∠3=180°.
a∥b
m∥l
n∥l
4
1
2
3
5
6
7
8
D
C
B
E
A
F
1. 再识“三线八角”:
4对同位角
∠1和∠5,
∠2和∠6,
∠3和∠7,
∠4和∠8.
2对内错角
∠3和∠5,
∠6和∠4.
2对同旁内角
∠5和∠4,
∠3和∠6.
课堂小结
2. 两直线平行的条件
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行.
3. 本节课运用了哪些数学思想方法?
你有什么收获?
谢谢聆听
第7章 平面图形的认识(二)
第1课时
2020-2021学年度苏科版七年级下册
判断:
1.同一平面内,直线有平行和垂直两种位置关系
2.与一条直线平行的直线只有一条.
3.两条直线不相交,就叫做平行线.
(×)
(×)
(×)
复习旧知
如图,装修工人正在向墙上钉木条,如果木条b与墙壁的边缘垂直,那么木条a与墙壁的边缘所夹的角为多少度时,才能使木条a与木条b平行?
答: 木条 a 与墙壁的边缘也垂直时才能使木条a与木条b平行.
平行在日常生活中的应用
如图,三根木条相交成∠1、∠2,固定木条b、c,转动木条a ,在木条a的转动过程中,∠1与∠2的大小关系发生了什么变化?木条a、b的位置关系发生了什么变化?
探索活动1:
1
2
b
a
c
探究新知
1
2
b
a
c
改变图中∠1的大小,按照上面的方式再试一试,当∠2与∠1的大小满足什么关系时,木条a与木条b平行?
探索活动1:
∠1>∠2
a、b不平行
∠1=∠2
a∥b
∠1<∠2
a、b不平行
1
2
1
2
1
2
b
a
b
b
a
a
∠1、∠2是 角
探索活动1:
3
4
5
6
7
8
1
2
a
b
c
1.观察∠1 与∠2的位置特点?
具有∠1与∠2这样位置关系的角,称为同位角.
3.图中还有同位角吗?
2、观察∠1 与∠2的边的特点?
我们把具有∠1与∠2这样位置关系的角称为同位角.
两直线AB、CD被第三直线EF所截,构成了八个角.
同 位 角 的 定 义
慧眼金睛:学会从复杂图形中分解出简单图形
图中有哪些同位角?请你找出来.
F
1
3
7
5
2
4
8
6
D
C
A
B
E
①
②
③
④
2
1
4
3
7
6
5
8
右上
左上
左下
右下
同位角是 F 形状
判断两条直线平行的方法:
由此可得:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线互相平行.
F
1
2
3
4
5
6
7
8
D
C
A
B
E
探索活动
你能找到一对同位角吗?
★ 在判别“同位角”时,要注意“两同”:在第三条直线的同旁;在被截两条直线的同一方向.
解:在图7-5中,AB∥CD,AC∥BD.
因为∠1与∠C是AB、CD被AC截成的同位角,且∠1=∠C,
所以AB∥CD.
理由是:同位角相等,两直线平行.
因为∠2与∠C是BD、AC被CD截成的同位角,且∠2=∠C,
所以AC//BD.
理由是:同位角相等,两直线平行.
例1 如图7-5,∠1=∠C,∠2=∠C.指出图中互相平行的直线,并说明理由.
典例讲解
知识加油站
1. 图中∠3与∠5,∠4与∠6这样位置关系的角有什么特点?说说你的理由.
2. ∠3与∠6,∠4与∠5这样位置关系的角呢?说说你的理由.
a
b
c
1
2
3
4
5
6
7
8
∠3与∠5,∠4与∠6这样位置关系的角,在两条被截直线的内部,在截线的两侧,位置是交错的,
这样的角叫做内错角.
∠3与∠6,∠4与∠5这样位置关系的角,在两条被截直线的内部,在截线的同旁,这样的角叫做同旁内角.
1. 观察右图并填空:
(1)∠1 与 是同位角;
(2)∠5 与 是同旁内角;
(3)∠1 与 是内错角.
∠4
∠3
∠2
b
a
n
m
2
3
1
4
5
针对练习
4
1
2
3
5
6
7
8
D
C
B
E
A
F
2. 如图,直线AB,CD被EF所截,构成了八个角,你能找出哪些角是同位角、内错角、同旁内角吗?
议一议
探索直线平行的条件
(一)内错角满足什么关系时?两直线平行?
(二)同旁内角满足什么关系时?两直线平行?
内错角相等,两直线平行.
同旁内角互补,两直线平行.
为什么?
为什么?
做一做:你能用三块大小相同的三角板(30°,60°,90°)拼接成一个含有平行线段的图形吗?试一试,多拼几个图形,找出平行线段后,说明你的理由.
1.图中各角分别满足下列条件时,你能判断哪两条直线平行吗?
①∠1=∠4 ②∠2=∠4 ③∠1+∠3=180°
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
针对练习
例2 如图7-9, ∠ 1=∠2,∠B+ ∠ BDE=180 °.指出图中互相平行的直线,并说明理由.
因为∠ B与∠ BDE是BC、DE被AB截成的同旁内角,且∠ B+∠ BDE=180°,
所以DE ∥BC.
理由是:同旁内角互补,两直线平行.
解:在图7-9中,AB ∥ EF,DE ∥ BC.
因为∠1与∠2是AB、EF被DE截成的内错角,
且∠1=∠2,
所以AB ∥ EF.
理由是:内错角相等,两直线平行.
典例讲解
例、如图,∠1=∠2=55°,∠3等于多少度?直线AB、CD平行吗?说明你的理由.
第2题图
3
1
2
A
B
F
C
D
E
∵∠2=55°
∴∠3=∠2=55°
∴∠3=∠1=55°
∴AB∥CD.
( )
对顶角相等
解: AB∥CD. 理由如下:
(已知)
(等量代换)
(同位角相等,两直线平行)
∵∠1= 55°
(已知)
1.找出下面点阵 (点阵中相邻的四个点构成正方形) 中互相平行的线段.
① AB∥CD
② EF∥GH
∵ ∠AMP=∠CPF
∵ ∠AMP=∠ANQ
E
G
B
D
F
H
A
C
M
N
P
Q
同位角相等,两直线平行.
同位角相等,两直线平行.
2.如图,∠1=∠2,直线AB,CD平行吗?
A
B
C
D
2
1
3
∵∠1=55°;
对顶角相等.
∴∠3=55°;
∵∠3 =∠2=55°;
∴ AB∥CD.
1.观察右图并填空:
∠1与 是同位角;
∠5与 是同旁内角;
(3) ∠2与 是内错角.
∠4
∠3
∠1
2.当图中各角分别满足下列条件时,你能支出哪两条直线平行吗?
∠1=∠4;
(2) ∠2=∠4;
(3)∠1+∠3=180°.
a∥b
m∥l
n∥l
4
1
2
3
5
6
7
8
D
C
B
E
A
F
1. 再识“三线八角”:
4对同位角
∠1和∠5,
∠2和∠6,
∠3和∠7,
∠4和∠8.
2对内错角
∠3和∠5,
∠6和∠4.
2对同旁内角
∠5和∠4,
∠3和∠6.
课堂小结
2. 两直线平行的条件
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行.
3. 本节课运用了哪些数学思想方法?
你有什么收获?
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
