7.1 探索直线平行的条件(第2课时)(共32张PPT)
文档属性
| 名称 | 7.1 探索直线平行的条件(第2课时)(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览




文档简介
第2课时
7.1 探索直线平行的条件
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
(1)平面内两条直线的位置关系有几种?
(2)怎样过已知直线外一点画已知直线的平行线?
相交与平行
复习提问
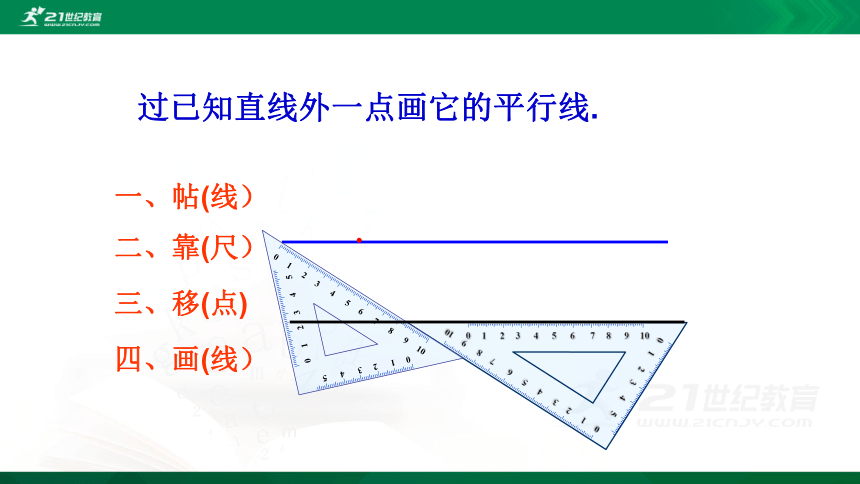
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
5
1
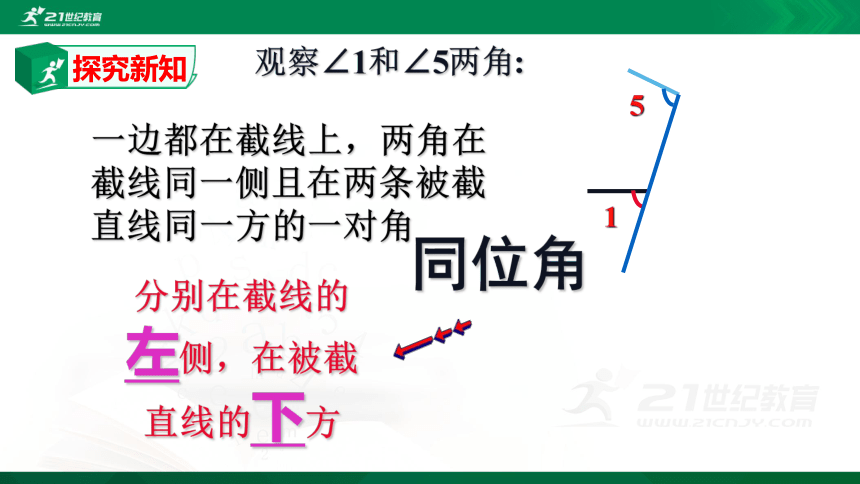
一边都在截线上,两角在截线同一侧且在两条被截直线同一方的一对角
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
探究新知
1
注意观察!
a
b
.
P
2
如何画平行线?
刚才的画法中,三角板起着什么作用?
想一想!
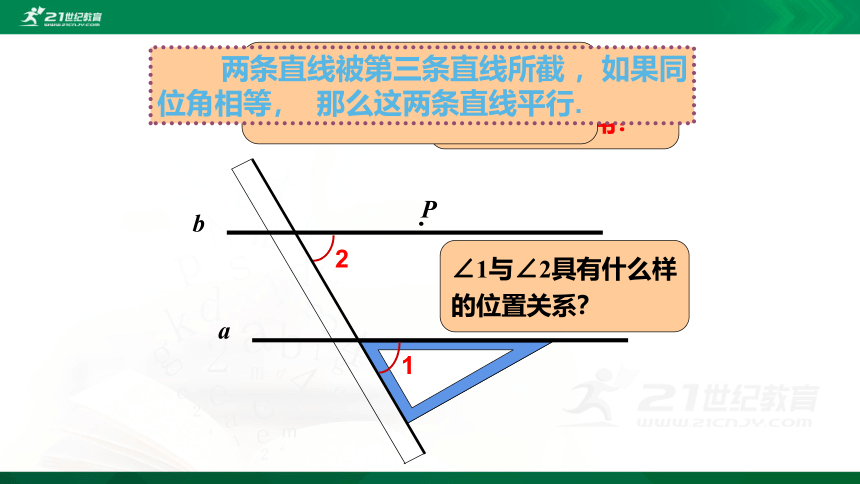
∠1与∠2具有什么样的位置关系?
我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.
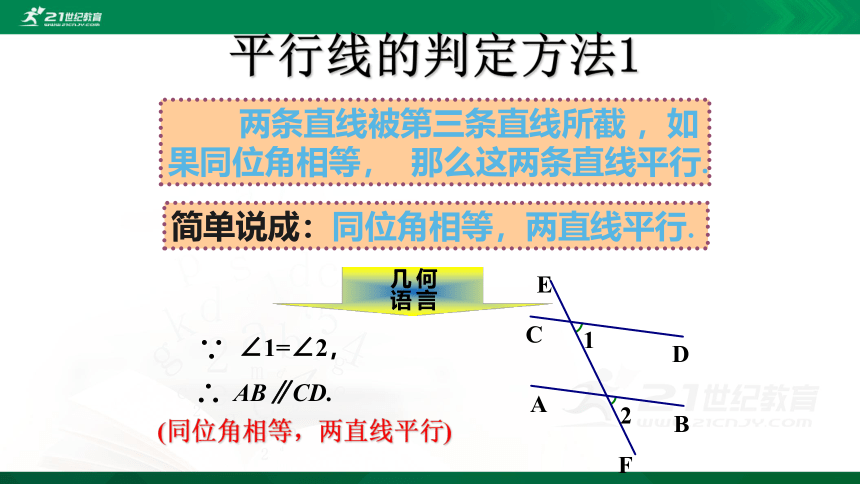
平行线的判定方法1
简单说成:同位角相等,两直线平行.
何言
几语
(同位角相等,两直线平行)
?
∠1=∠2,
?
AB∥CD.
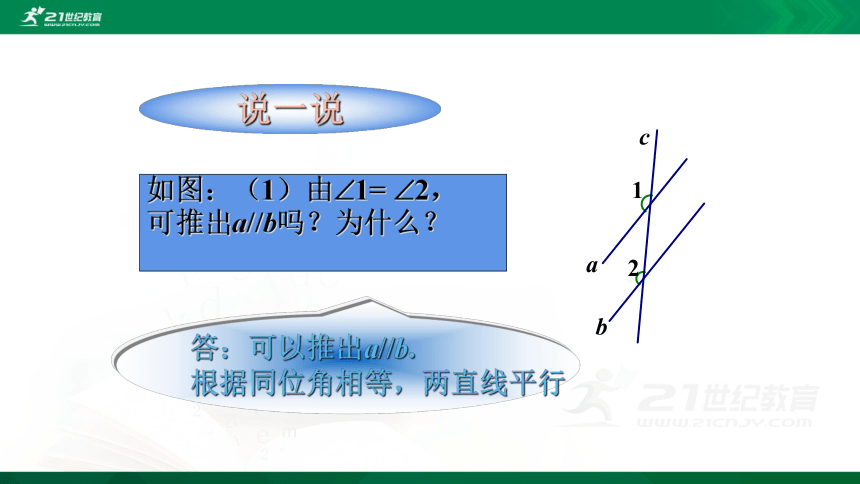
如图:(1)由?1= ?2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行
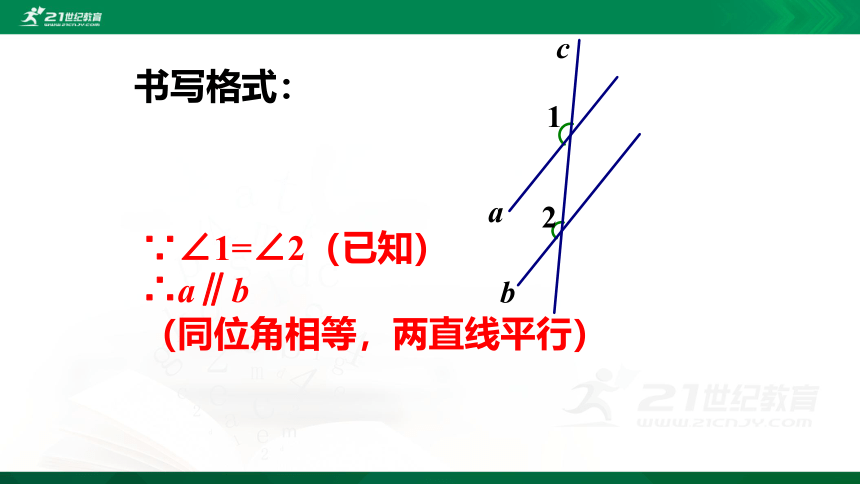
∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
书写格式:
解:在图7-5中,AB∥CD,AC∥BD.
因为∠1与∠C是AB、CD被AC截成的同位角,且∠1=∠C,
所以AB∥CD.
理由是:同位角相等,两直线平行.
因为∠2与∠C是BD、AC被CD截成的同位角,且∠2=∠C,
所以AC//BD.
理由是:同位角相等,两直线平行.
例1 如图7-5,∠1=∠C,∠2=∠C.指出图中互相平行的直线,并说明理由.
例题讲解
1.如图,哪两个角相等能判定直线AB∥CD?
D
B
4
3
1
4
3
2
A
C
理解运用
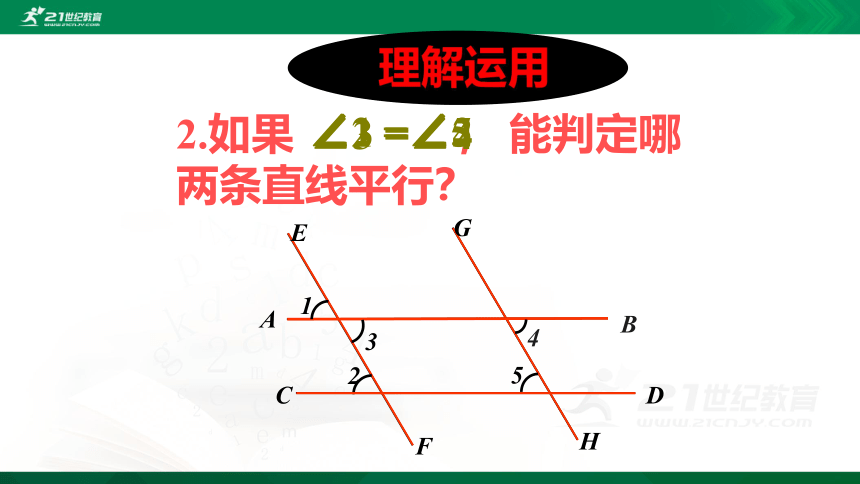
2.如果 , 能判定哪两条直线平行?
∠1 =∠2
A
B
C
E
F
D
2
5
H
G
4
1
3
∠3 =∠4
∠2 =∠5
理解运用
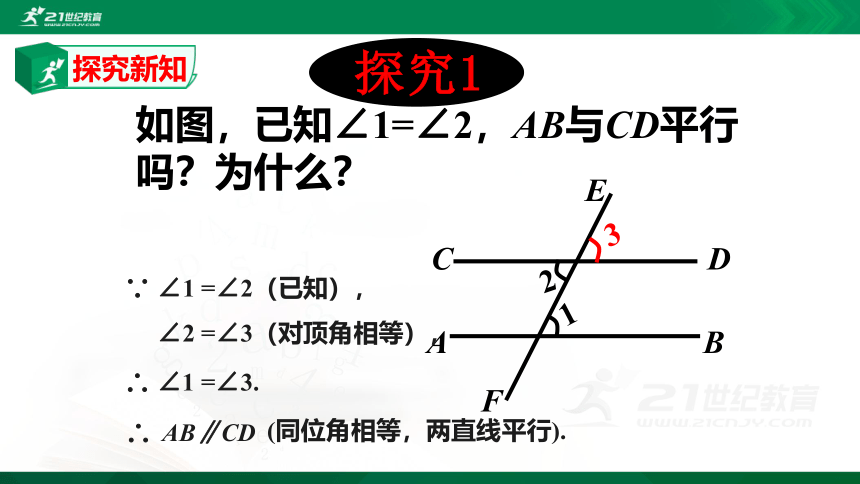
如图,已知∠1=∠2,AB与CD平行吗?为什么?
探究1
A
B
C
D
E
F
1
2
3
?
∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
?
∠1 =∠3.
?
AB∥CD
(同位角相等,两直线平行).
探究新知
一边都在截线上,两角在截线的两侧且在两条被截直线之间的一对角
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线内,分别在截线两侧(交错)
两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
?
∠1=∠2,
?
AB∥CD.
如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
想一想
练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么?
针对练习
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(内错角相等,两直线平行).
探究2
3
探究新知
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
3
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(同位角相等,两直线平行).
探究2
一边都在截线上,两角在截线的同侧且在两条被截直线之间的一对角
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两被截直线内
探究新知
两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
何言
几语
(同旁内角互补,两直线平行)
A
B
C
D
E
F
1
2
?
∠1+∠2=180°,
?
AB∥CD.
如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?
答:AB//CD,AD//BC
∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
D
C
B
A
想一想
例2 如图7-9, ∠ 1=∠2,∠B+ ∠ BDE=180 °.指出图中互相平行的直线,并说明理由.
因为∠ B与∠ BDE是BC、DE被AB截成的同旁内角,且∠ B+∠ BDE=180°,
所以DE ∥BC.
理由是:同旁内角互补,两直线平行.
解:在图7-9中,AB ∥ EF,DE ∥ BC.
因为∠1与∠2是AB、EF被DE截成的内错角,
且∠1=∠2,
所以AB ∥ EF.
理由是:内错角相等,两直线平行.
例题讲解
1.如图,∠1与∠C、∠2与∠B、∠3与∠C分别是哪两条直线被哪一条直线截成的同位角?
∠1与∠C是DE、BC被AC所截形成的同位角;
∠2与∠B是DE、BC被AB所截形成的同位角;
∠3与∠C是DF、AC被BC所截形成的同位角.
针对练习
2.(1)如图①,
因为∠1+∠A=90°,∠1+∠2=90°,
所以∠A=∠_____.
理由是:__________________________.
(2)如图②,
因为∠A=∠DEC,
所以_____∥_______.
理由是:_____________________________.
2
与同角成余角 的角相等
AB
DE
同位角相等,两直线平行
3.如图,∠ADE=60°,∠ABE=30°.
(1)当∠ABC等于多少度时,DE∥BC?为什么?
(2)当∠ADF等于多少度时,DF∥BE?为什么?
(1)∠ABC=60°时,DE∥BC.同位角相等,两直线平行.
(2)∠ADF=30°时,DF∥BE.同位角相等,两直线平行.
1.如图,∠1与∠B、∠3与∠4、∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
∠1与∠B是AC、BD被BE所截形成的同位角;
∠3与∠4是EB、CD被AD所截形成的内错角;
∠2与∠4是AC、CD被AD所截形成的同旁内角.
课堂练习
2. 如图,
(1)因为∠1=∠2,
所以_____∥_______.
理由是:__________________________.
(2)因为∠2=________,
所以AD∥BE.
理由是:_____________________________.
(1)因为∠1+∠B=180°,
所以_____∥_______.
理由是:__________________________.
∠DEB
内错角相等,两直线平行
AB
CE
同位角相等,两直线平行
AD
BE
同旁内角互补,两直线平行
3.如图,直线AB与射线DE相交于点O,∠BOE
=130°,∠D=50°.AB与CD平行吗?为什么?
解:∵∠BOE=130°,
∴∠EOA=50°.
∴∠EOA=∠D.
∴AB∥CD.(同位角相等,两直线平行)
判定两条直线平行的方法
文字叙述
符号语言
图形
相等
两直线平行
∵ (已知)
∴a∥b
相等
两直线平行
∵ (已知)
∴a∥b
互补,两直线平行
∵
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
课堂小结
谢谢聆听
7.1 探索直线平行的条件
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
(1)平面内两条直线的位置关系有几种?
(2)怎样过已知直线外一点画已知直线的平行线?
相交与平行
复习提问
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
5
1
一边都在截线上,两角在截线同一侧且在两条被截直线同一方的一对角
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
探究新知
1
注意观察!
a
b
.
P
2
如何画平行线?
刚才的画法中,三角板起着什么作用?
想一想!
∠1与∠2具有什么样的位置关系?
我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.
平行线的判定方法1
简单说成:同位角相等,两直线平行.
何言
几语
(同位角相等,两直线平行)
?
∠1=∠2,
?
AB∥CD.
如图:(1)由?1= ?2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行
∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
书写格式:
解:在图7-5中,AB∥CD,AC∥BD.
因为∠1与∠C是AB、CD被AC截成的同位角,且∠1=∠C,
所以AB∥CD.
理由是:同位角相等,两直线平行.
因为∠2与∠C是BD、AC被CD截成的同位角,且∠2=∠C,
所以AC//BD.
理由是:同位角相等,两直线平行.
例1 如图7-5,∠1=∠C,∠2=∠C.指出图中互相平行的直线,并说明理由.
例题讲解
1.如图,哪两个角相等能判定直线AB∥CD?
D
B
4
3
1
4
3
2
A
C
理解运用
2.如果 , 能判定哪两条直线平行?
∠1 =∠2
A
B
C
E
F
D
2
5
H
G
4
1
3
∠3 =∠4
∠2 =∠5
理解运用
如图,已知∠1=∠2,AB与CD平行吗?为什么?
探究1
A
B
C
D
E
F
1
2
3
?
∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
?
∠1 =∠3.
?
AB∥CD
(同位角相等,两直线平行).
探究新知
一边都在截线上,两角在截线的两侧且在两条被截直线之间的一对角
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线内,分别在截线两侧(交错)
两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
?
∠1=∠2,
?
AB∥CD.
如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
想一想
练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么?
针对练习
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(内错角相等,两直线平行).
探究2
3
探究新知
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
3
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(同位角相等,两直线平行).
探究2
一边都在截线上,两角在截线的同侧且在两条被截直线之间的一对角
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两被截直线内
探究新知
两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
何言
几语
(同旁内角互补,两直线平行)
A
B
C
D
E
F
1
2
?
∠1+∠2=180°,
?
AB∥CD.
如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?
答:AB//CD,AD//BC
∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
D
C
B
A
想一想
例2 如图7-9, ∠ 1=∠2,∠B+ ∠ BDE=180 °.指出图中互相平行的直线,并说明理由.
因为∠ B与∠ BDE是BC、DE被AB截成的同旁内角,且∠ B+∠ BDE=180°,
所以DE ∥BC.
理由是:同旁内角互补,两直线平行.
解:在图7-9中,AB ∥ EF,DE ∥ BC.
因为∠1与∠2是AB、EF被DE截成的内错角,
且∠1=∠2,
所以AB ∥ EF.
理由是:内错角相等,两直线平行.
例题讲解
1.如图,∠1与∠C、∠2与∠B、∠3与∠C分别是哪两条直线被哪一条直线截成的同位角?
∠1与∠C是DE、BC被AC所截形成的同位角;
∠2与∠B是DE、BC被AB所截形成的同位角;
∠3与∠C是DF、AC被BC所截形成的同位角.
针对练习
2.(1)如图①,
因为∠1+∠A=90°,∠1+∠2=90°,
所以∠A=∠_____.
理由是:__________________________.
(2)如图②,
因为∠A=∠DEC,
所以_____∥_______.
理由是:_____________________________.
2
与同角成余角 的角相等
AB
DE
同位角相等,两直线平行
3.如图,∠ADE=60°,∠ABE=30°.
(1)当∠ABC等于多少度时,DE∥BC?为什么?
(2)当∠ADF等于多少度时,DF∥BE?为什么?
(1)∠ABC=60°时,DE∥BC.同位角相等,两直线平行.
(2)∠ADF=30°时,DF∥BE.同位角相等,两直线平行.
1.如图,∠1与∠B、∠3与∠4、∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
∠1与∠B是AC、BD被BE所截形成的同位角;
∠3与∠4是EB、CD被AD所截形成的内错角;
∠2与∠4是AC、CD被AD所截形成的同旁内角.
课堂练习
2. 如图,
(1)因为∠1=∠2,
所以_____∥_______.
理由是:__________________________.
(2)因为∠2=________,
所以AD∥BE.
理由是:_____________________________.
(1)因为∠1+∠B=180°,
所以_____∥_______.
理由是:__________________________.
∠DEB
内错角相等,两直线平行
AB
CE
同位角相等,两直线平行
AD
BE
同旁内角互补,两直线平行
3.如图,直线AB与射线DE相交于点O,∠BOE
=130°,∠D=50°.AB与CD平行吗?为什么?
解:∵∠BOE=130°,
∴∠EOA=50°.
∴∠EOA=∠D.
∴AB∥CD.(同位角相等,两直线平行)
判定两条直线平行的方法
文字叙述
符号语言
图形
相等
两直线平行
∵ (已知)
∴a∥b
相等
两直线平行
∵ (已知)
∴a∥b
互补,两直线平行
∵
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
课堂小结
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
