7.2 探索平行线的性质同步练习(含解析)
文档属性
| 名称 | 7.2 探索平行线的性质同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 13:39:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
7.2 探索平行线的性质练习
一、单选题(共10小题)
1.(2020·江苏苏州市·七年级期末)如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
A.48° B.78° C.92° D.102°
2.(2020·江苏南京市·七年级期末)如图,若,则下列结论正确的是( )
A. B. C. D.∠2=∠4
3.(2020·江苏泰州市·七年级期中)如图,AD∥CE,∠ABC=95°,则∠2﹣∠1的度数是( )
A.105° B.95° C.85° D.75°
4.(2020·江苏淮安市·七年级期末)如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
A.70° B.68° C.60° D.72°
5.(2020·江苏扬州市·七年级期末)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为( )
A.45° B.55° C.65° D.75°
6.(2020·江苏扬州市·七年级期末)如图,a∥b,若∠1=110°,则∠2的度数是( )
A.110° B.80° C.70° D.60°
7.(2020·江苏扬州市·七年级期末)如图,直线a,b被直线c所截,a∥b,若∠2=45°,则∠1等于( )
A.125° B.130° C.135° D.145°
8.(2020·江苏苏州市·七年级期末)如图,在△ABC中,∠ABC=60°,点C在直线b上,若直线a∥b,∠2=26°,则∠1的度数为( )
A.26° B.28° C.34° D.36°
9.(2020·江苏徐州市·七年级期末)将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①如果,则;
②;
③如果则;
④如果,则.其中正确的结论有( )
A.个 B.个 C.个 D.个
10.(2020·江苏徐州市·七年级期中)如图,下列结论中不正确的是( )
A.若∠1=∠2,则AD∥BC B.若AE∥CD,则∠1+∠3=180°
C.若∠2=∠C,则AE∥CD D.若AD∥BC,则∠1=∠B
二、填空题(共5小题)
11.(2020·江苏扬州市·七年级期末)如图,把一个长方形纸片沿折叠后,点,分别落在,的位置,若,则’等于__________.
12.(2020·江苏宿迁市·七年级期中)如图,请在下列空格内填写结论和理由.
已知:,
试说明:
证明:
____________(_________________)
(____________________)
___________
(______________________________)
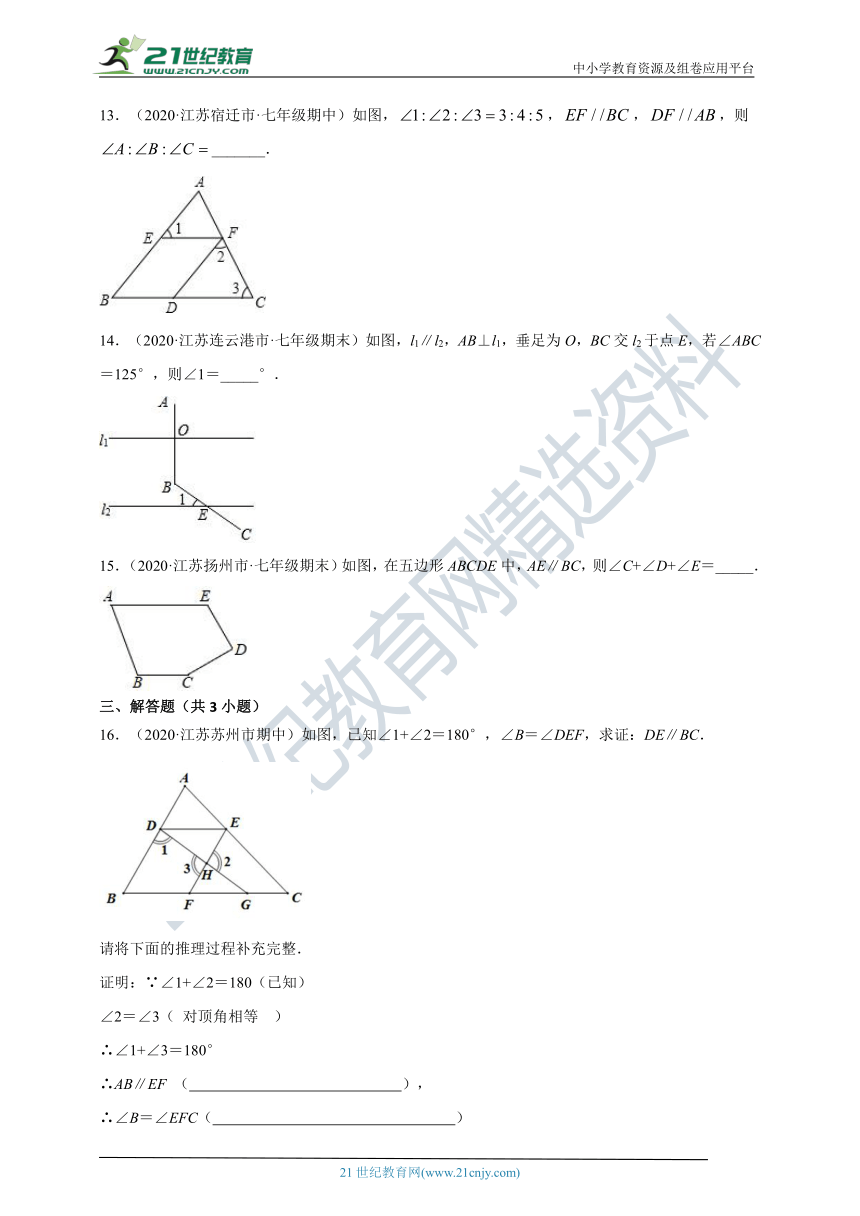
13.(2020·江苏宿迁市·七年级期中)如图,,,,则_______.
14.(2020·江苏连云港市·七年级期末)如图,l1∥l2,AB⊥l1,垂足为O,BC交l2于点E,若∠ABC=125°,则∠1=_____°.
15.(2020·江苏扬州市·七年级期末)如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=_____.
三、解答题(共3小题)
16.(2020·江苏苏州市期中)如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
请将下面的推理过程补充完整.
证明:∵∠1+∠2=180(已知)
∠2=∠3( 对顶角相等 )
∴∠1+∠3=180°
∴AB∥EF ( ),
∴∠B=∠EFC( )
∵∠B=∠DEF( ),
∴∠DEF= ( )
∴DE∥BC( )
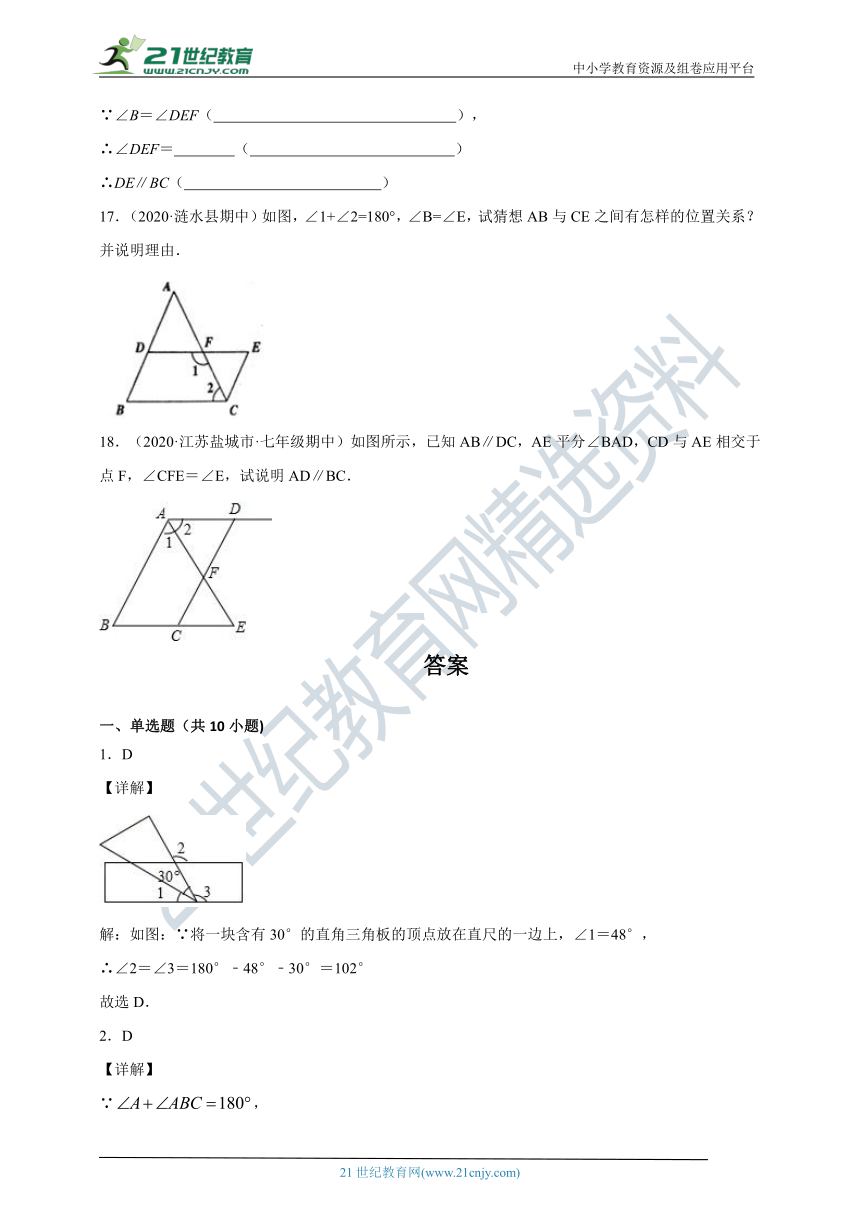
17.(2020·涟水县期中)如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
18.(2020·江苏盐城市·七年级期中)如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.
答案
一、单选题(共10小题)
1.D
【详解】
解:如图:∵将一块含有30°的直角三角板的顶点放在直尺的一边上,∠1=48°,
∴∠2=∠3=180°﹣48°﹣30°=102°
故选D.
2.D
【详解】
∵,
∴AD∥BC,
∴∠2=∠4,
故选:D.
3.C
【详解】
解:作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°①,
∵∠3+∠4=95°,
∴∠1+∠4=95°②,
①-②,得
∠2-∠1=85°.
故选C.
4.A
【详解】
解:∵AB∥CD,∠C=35°,
∴∠ABC=∠C=35°.
∵BC平分∠ABE,
∴∠ABE=2∠ABC=70°.
∵AB∥CD,
∴∠BED=∠ABE=70°.
故选A.
5.C
【详解】
解:如图,过直角顶点O作EF∥AB,由于AB∥CD,则EF∥AB∥CD,
∴∠2=∠3,∠1=∠4,
∵∠2=25°,
∴∠3=25°,
∵∠3+∠4=90°,
∴∠4=65°,
∴∠1=65°.
故选:C.
6.C
【详解】
解:∵a∥b,
∴∠1=∠3=110°.
∵∠2+∠3=180°,
∴∠2=180°﹣∠3=70°,
故选:C.
7.C
【详解】
如图,
∵a∥b,∠2=45°,
∴∠3=∠2=45°,
∴∠1=180°?∠3=135°,
故选:C.
8.C
【详解】
如图,过点B作BE∥a.
∵a∥b,a∥BE,
∴b∥BE,
∴∠1=∠ABE,∠2=∠CBE,
∵∠ABC=∠ABE+∠CBE=60°,
∴∠1+∠2=60°,
∵∠2=26°,
∴∠1=34°,
故选:C.
9.C
【详解】
①如果,则∠1=90°-=∠E
∴,正确;
②,正确;
③如果则∠3=∠B=45°
∴,故错误;
④如果,则∠1==∠E,正确
故选C.
10.D
【详解】
解:A、∵∠1=∠2,
∴AD∥BC,原结论正确,故此选项不符合题意;
B、∵AE∥CD,
∴∠1+∠3=180°,原结论正确,故此选项不符合题意;
C、∵∠2=∠C,
∴AE∥CD,原结论正确,故此选项不符合题意;
D、∵AD∥BC,
∴∠1=∠2,原结论不正确,故此选项符合题意;
故选:D.
二、填空题(共5小题)
11.
【详解】
∵AD∥BC,
∴∠DEF=∠EFB=68°,
∵长方形纸片沿EF折叠后,点DC分别落在点D′、C′的位置,
∴∠D′EF=∠DEF=68°,
∴∠AED′=180°?∠D′EF?∠DEF=180°?2×68°=44°.
故答案为44°.
12.AD;BE;内错角相等,两直线平行;两直线平行,同旁内角互补;B;2;同旁内角互补,两直线平行.
【详解】
解:证明:∵∠1=∠E,
∴AD∥BE(内错角相等,两直线平行),
∴∠D+∠2=180°(两直线平行,同旁内角互补),
∵∠B=∠D,
∴∠B+∠2=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:AD;BE;内错角相等,两直线平行;两直线平行,同旁内角互补;B;2;同旁内角互补,两直线平行.
13.4:3:5
【详解】
解:∵∠1:∠2:∠3=3:4:5,
∴设∠1=3x,则∠2=4x,∠3=5x,
∵EF∥BC,
∴∠B=∠1=3x,
∵DF∥AB,
∴∠FDC=∠B=3x,
在△FDC中,
∵∠FDC+∠2+∠3=180°,即3x+4x+5x=180°,解得x=15°,
∴∠B=3x=45°,∠A=∠2=4x=60°,
∴∠C=180°-∠B-∠A=180°-45°-60°=75°,
∴∠A:∠B:∠C=60:45:75=4:3:5.
故答案为:4:3:5.
14.35.
【详解】
过B作BF∥l2,
∵l1∥l2,
∴BF∥l1∥l2,
∴∠ABF=∠2,∠1=∠FBC,
∵AB⊥l1,
∴∠2=90°,
∴∠ABF=90°,
∵∠ABC=125°,
∴∠FBC=35°,
∴∠1=35°,
故答案为:35.
15.360°
【详解】
解:过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
三、解答题(共3小题)
16.【详解】
解:证明:∵∠1+∠2=180(已知),
∠2=∠3(对顶角相等),
∴∠1+∠3=180°,
∴AB∥EF (同旁内角互补,两直线平行),
∴∠B=∠EFC(两直线平行,同位角相等),
∵∠B=∠DEF(已知),
∴∠DEF=∠EFC(等量代换),
∴DE∥BC(内错角相等,两直线平行).
17.AB//CE,理由见解析
解:AB//CE,理由如下:
∵∠1+∠2=180°,
∴DE//BC(同旁内角互补,两直线平行),
∴∠ADF=∠B(两直线平行,同位角相等) ,
∵∠B=∠E,
∴∠ADF=∠E,
∴AB//CE(内错角相等,两直线平行).
18.【详解】
解:∵AB∥CD,
∴∠BAE=∠CFE,
∵AE平分∠BAD,
∴∠BAE=∠DAF,
∵∠CFE=∠E,
∴∠DAF=∠E,
∴AD∥BC.
_21?????????è?????(www.21cnjy.com)_
7.2 探索平行线的性质练习
一、单选题(共10小题)
1.(2020·江苏苏州市·七年级期末)如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
A.48° B.78° C.92° D.102°
2.(2020·江苏南京市·七年级期末)如图,若,则下列结论正确的是( )
A. B. C. D.∠2=∠4
3.(2020·江苏泰州市·七年级期中)如图,AD∥CE,∠ABC=95°,则∠2﹣∠1的度数是( )
A.105° B.95° C.85° D.75°
4.(2020·江苏淮安市·七年级期末)如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
A.70° B.68° C.60° D.72°
5.(2020·江苏扬州市·七年级期末)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为( )
A.45° B.55° C.65° D.75°
6.(2020·江苏扬州市·七年级期末)如图,a∥b,若∠1=110°,则∠2的度数是( )
A.110° B.80° C.70° D.60°
7.(2020·江苏扬州市·七年级期末)如图,直线a,b被直线c所截,a∥b,若∠2=45°,则∠1等于( )
A.125° B.130° C.135° D.145°
8.(2020·江苏苏州市·七年级期末)如图,在△ABC中,∠ABC=60°,点C在直线b上,若直线a∥b,∠2=26°,则∠1的度数为( )
A.26° B.28° C.34° D.36°
9.(2020·江苏徐州市·七年级期末)将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①如果,则;
②;
③如果则;
④如果,则.其中正确的结论有( )
A.个 B.个 C.个 D.个
10.(2020·江苏徐州市·七年级期中)如图,下列结论中不正确的是( )
A.若∠1=∠2,则AD∥BC B.若AE∥CD,则∠1+∠3=180°
C.若∠2=∠C,则AE∥CD D.若AD∥BC,则∠1=∠B
二、填空题(共5小题)
11.(2020·江苏扬州市·七年级期末)如图,把一个长方形纸片沿折叠后,点,分别落在,的位置,若,则’等于__________.
12.(2020·江苏宿迁市·七年级期中)如图,请在下列空格内填写结论和理由.
已知:,
试说明:
证明:
____________(_________________)
(____________________)
___________
(______________________________)
13.(2020·江苏宿迁市·七年级期中)如图,,,,则_______.
14.(2020·江苏连云港市·七年级期末)如图,l1∥l2,AB⊥l1,垂足为O,BC交l2于点E,若∠ABC=125°,则∠1=_____°.
15.(2020·江苏扬州市·七年级期末)如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=_____.
三、解答题(共3小题)
16.(2020·江苏苏州市期中)如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
请将下面的推理过程补充完整.
证明:∵∠1+∠2=180(已知)
∠2=∠3( 对顶角相等 )
∴∠1+∠3=180°
∴AB∥EF ( ),
∴∠B=∠EFC( )
∵∠B=∠DEF( ),
∴∠DEF= ( )
∴DE∥BC( )
17.(2020·涟水县期中)如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
18.(2020·江苏盐城市·七年级期中)如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.
答案
一、单选题(共10小题)
1.D
【详解】
解:如图:∵将一块含有30°的直角三角板的顶点放在直尺的一边上,∠1=48°,
∴∠2=∠3=180°﹣48°﹣30°=102°
故选D.
2.D
【详解】
∵,
∴AD∥BC,
∴∠2=∠4,
故选:D.
3.C
【详解】
解:作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°①,
∵∠3+∠4=95°,
∴∠1+∠4=95°②,
①-②,得
∠2-∠1=85°.
故选C.
4.A
【详解】
解:∵AB∥CD,∠C=35°,
∴∠ABC=∠C=35°.
∵BC平分∠ABE,
∴∠ABE=2∠ABC=70°.
∵AB∥CD,
∴∠BED=∠ABE=70°.
故选A.
5.C
【详解】
解:如图,过直角顶点O作EF∥AB,由于AB∥CD,则EF∥AB∥CD,
∴∠2=∠3,∠1=∠4,
∵∠2=25°,
∴∠3=25°,
∵∠3+∠4=90°,
∴∠4=65°,
∴∠1=65°.
故选:C.
6.C
【详解】
解:∵a∥b,
∴∠1=∠3=110°.
∵∠2+∠3=180°,
∴∠2=180°﹣∠3=70°,
故选:C.
7.C
【详解】
如图,
∵a∥b,∠2=45°,
∴∠3=∠2=45°,
∴∠1=180°?∠3=135°,
故选:C.
8.C
【详解】
如图,过点B作BE∥a.
∵a∥b,a∥BE,
∴b∥BE,
∴∠1=∠ABE,∠2=∠CBE,
∵∠ABC=∠ABE+∠CBE=60°,
∴∠1+∠2=60°,
∵∠2=26°,
∴∠1=34°,
故选:C.
9.C
【详解】
①如果,则∠1=90°-=∠E
∴,正确;
②,正确;
③如果则∠3=∠B=45°
∴,故错误;
④如果,则∠1==∠E,正确
故选C.
10.D
【详解】
解:A、∵∠1=∠2,
∴AD∥BC,原结论正确,故此选项不符合题意;
B、∵AE∥CD,
∴∠1+∠3=180°,原结论正确,故此选项不符合题意;
C、∵∠2=∠C,
∴AE∥CD,原结论正确,故此选项不符合题意;
D、∵AD∥BC,
∴∠1=∠2,原结论不正确,故此选项符合题意;
故选:D.
二、填空题(共5小题)
11.
【详解】
∵AD∥BC,
∴∠DEF=∠EFB=68°,
∵长方形纸片沿EF折叠后,点DC分别落在点D′、C′的位置,
∴∠D′EF=∠DEF=68°,
∴∠AED′=180°?∠D′EF?∠DEF=180°?2×68°=44°.
故答案为44°.
12.AD;BE;内错角相等,两直线平行;两直线平行,同旁内角互补;B;2;同旁内角互补,两直线平行.
【详解】
解:证明:∵∠1=∠E,
∴AD∥BE(内错角相等,两直线平行),
∴∠D+∠2=180°(两直线平行,同旁内角互补),
∵∠B=∠D,
∴∠B+∠2=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:AD;BE;内错角相等,两直线平行;两直线平行,同旁内角互补;B;2;同旁内角互补,两直线平行.
13.4:3:5
【详解】
解:∵∠1:∠2:∠3=3:4:5,
∴设∠1=3x,则∠2=4x,∠3=5x,
∵EF∥BC,
∴∠B=∠1=3x,
∵DF∥AB,
∴∠FDC=∠B=3x,
在△FDC中,
∵∠FDC+∠2+∠3=180°,即3x+4x+5x=180°,解得x=15°,
∴∠B=3x=45°,∠A=∠2=4x=60°,
∴∠C=180°-∠B-∠A=180°-45°-60°=75°,
∴∠A:∠B:∠C=60:45:75=4:3:5.
故答案为:4:3:5.
14.35.
【详解】
过B作BF∥l2,
∵l1∥l2,
∴BF∥l1∥l2,
∴∠ABF=∠2,∠1=∠FBC,
∵AB⊥l1,
∴∠2=90°,
∴∠ABF=90°,
∵∠ABC=125°,
∴∠FBC=35°,
∴∠1=35°,
故答案为:35.
15.360°
【详解】
解:过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
三、解答题(共3小题)
16.【详解】
解:证明:∵∠1+∠2=180(已知),
∠2=∠3(对顶角相等),
∴∠1+∠3=180°,
∴AB∥EF (同旁内角互补,两直线平行),
∴∠B=∠EFC(两直线平行,同位角相等),
∵∠B=∠DEF(已知),
∴∠DEF=∠EFC(等量代换),
∴DE∥BC(内错角相等,两直线平行).
17.AB//CE,理由见解析
解:AB//CE,理由如下:
∵∠1+∠2=180°,
∴DE//BC(同旁内角互补,两直线平行),
∴∠ADF=∠B(两直线平行,同位角相等) ,
∵∠B=∠E,
∴∠ADF=∠E,
∴AB//CE(内错角相等,两直线平行).
18.【详解】
解:∵AB∥CD,
∴∠BAE=∠CFE,
∵AE平分∠BAD,
∴∠BAE=∠DAF,
∵∠CFE=∠E,
∴∠DAF=∠E,
∴AD∥BC.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
