贵州省贵阳市2020-2021学年高一上学期期末监测考试数学试题 Word版含答案
文档属性
| 名称 | 贵州省贵阳市2020-2021学年高一上学期期末监测考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 741.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:01:06 | ||
图片预览




文档简介
贵阳市普通中学2020—2021学年度第一学期期末监测考试
高一数学
注意事项:
1.本试卷满分100分,考试时间90分钟
2.试卷共10页,其中试题卷6页,答题卷4页,答题前请沿裁切线裁切
3.考试过程中不得使用计算器
一、选择题(本大题共10小题,每小题4分,共40分,每小题有四个选项,其中只有一个选项正确,请将你认为正确的选项填在答题卷的相应位置上。)
1、已知集合false,则false( )
A.false B.false C、false D、false
2、圆心角弧度数和半径均为2的扇形的弧长为( )
A.1 B、2 C、4 D、8
3、已知向量false,且false是共线向量,则实数false的值为( )
A.-4 B、false C、false D.0
4、化简false ( )
A、false B、false C、false D、false
5、设函数false,则f(10)=( )
A.0 B.false C.1 D、false
6、设false为锐角,且false,则false ( )
A.false B.false C.false D、1
7.下列函数中,既是偶函数,又在区间false上单调递增的是( )
A、false B、false C、false D.false
8、函数false的定义域是( )
A.(1,+∞) B、(2,+∞) C、false D、false
9、设false,则a,b,c大小的关系为( )
A. a10、设函数false,下列说法中,错误的是( )
A.false的最小值为false
B.false在区间false上单调递增
C.函数false的图像可由函数false的图像先向左平移false个单位,再将横坐标缩短为原来的一半(纵坐标不变)而得到
D.将函数y=f(x)的图像向左平移false个单位,所得函数的图像关于y轴对称
二、填空题(本大题共5小题,每小题4分,共20分。请将你认为正确的答案填在答题卷的相应位置上。)
11、若点false在幂函数false的图像上,则false
12计算false
13.设非零向量false满足false,则false与false的夹角为
14.false
false
15.以下条件
①a>b>1;②b>a>1
③1>a>b>0;④1>b>a>0
⑤a>1,1>b>0;⑥b>1,1>a>0
能够使得:false成立的有
三、解答题(本大题共4小题,每小题8分,共32分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分8分)
在平面直角坐标系中,已知角false的顶点都在坐标原点,始边都与x轴非负半轴重合,角false的终边上有一点A,坐标为(1,-1)
(1)求false的值;
(2)若角false满足下列三个条件之一
①锐角满足false
②锐角false的终边在直线false上;
③角false的终边与false的终边相同
请从上述三个条件中任选一个,你的选择是 ,求false的值。
17.(本小题满分8分)
设函数false为定义在R上的偶函数,当x≥0时,false。
(1)求函数false的解析式,并作出函数false的大致图象;
(2)判断函数false的零点个数(可结合图像判断)。
18、(本小题满分8分)
三角形ABC中,D为BC上一点,BD=2DC,设false,可以用false来表示出false,方法如下:
方法一:false
false
false
方法二:false
false
false
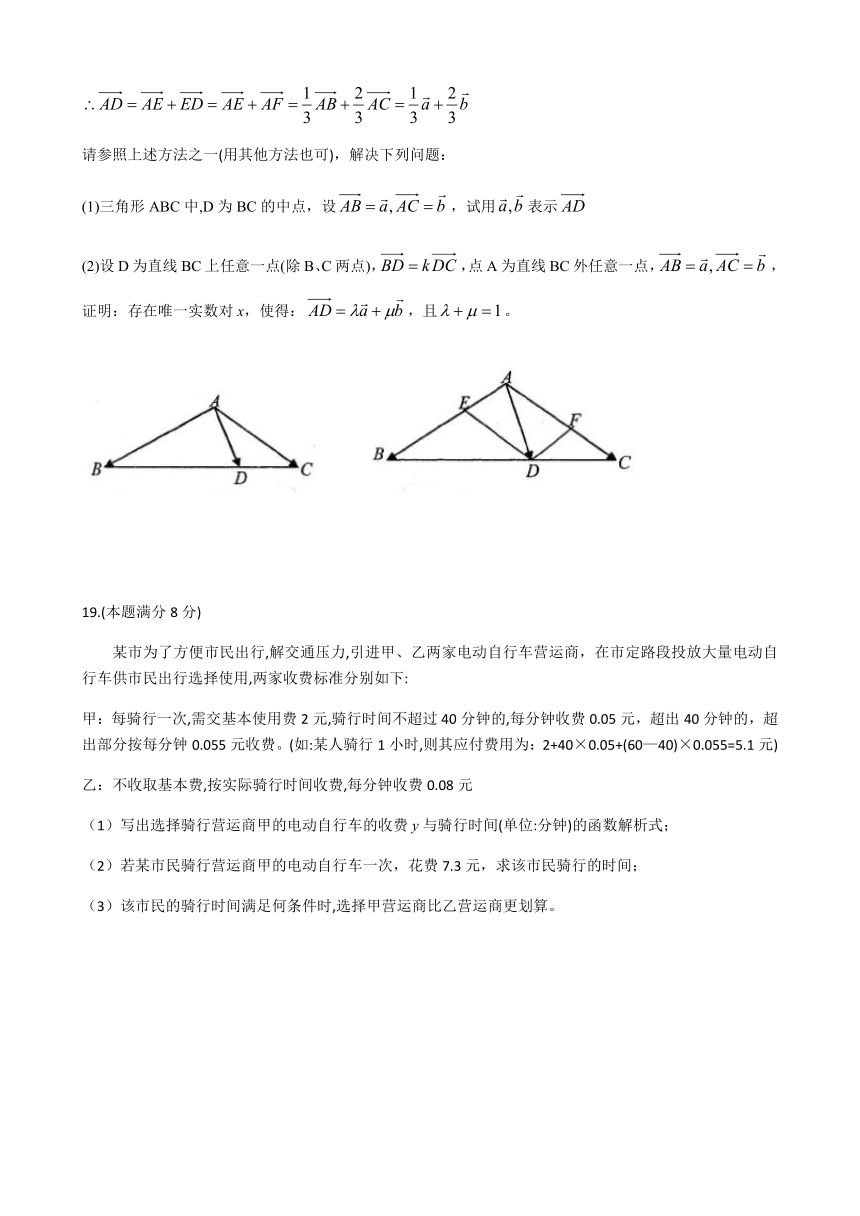
方法三:如图所示,过点D作AC的平行线交AB于点E,过点D作AB的平行线交AC于点F,则四边形AEDF为平行四边形
∵DF∥AB且BD=2DC,
false,false
∵ED∥AC,BD=2DC,
false
请参照上述方法之一(用其他方法也可),解决下列问题:
(1)三角形ABC中,D为BC的中点,设false,试用false表示false
(2)设D为直线BC上任意一点(除B、C两点),false,点A为直线BC外任意一点,false,证明:存在唯一实数对x,使得:false,且false。
19.(本题满分8分)
某市为了方便市民出行,解交通压力,引进甲、乙两家电动自行车营运商,在市定路段投放大量电动自行车供市民出行选择使用,两家收费标准分别如下:
甲:每骑行一次,需交基本使用费2元,骑行时间不超过40分钟的,每分钟收费0.05元,超出40分钟的,超出部分按每分钟0.055元收费。(如:某人骑行1小时,则其应付费用为:2+40×0.05+(60—40)×0.055=5.1元)
乙:不收取基本费,按实际骑行时间收费,每分钟收费0.08元
(1)写出选择骑行营运商甲的电动自行车的收费y与骑行时间(单位:分钟)的函数解析式;
(2)若某市民骑行营运商甲的电动自行车一次,花费7.3元,求该市民骑行的时间;
(3)该市民的骑行时间满足何条件时,选择甲营运商比乙营运商更划算。
四、阅读与探究(本大题1个小题,共8分。解答应写出文字说明,条理清晰。)
20.(本小题满分8分)
定义函数false为“正余弦”函数。结合学过的相关知识,我们可以得到该函数的性质。
1、我们知道,正弦函数y=sinx和余弦函数y=cosx的定义域均为R,故函数f(x)=cos(sinx)的定义域为R
2、我们知道,正弦函数y=sinx为奇函数,余弦函数y=cosx为偶函数,对f(x)=cos(sinx), false,可得:函数f(x)=cos(sinx)为偶函数
3、我们知道,正弦函数y=sinx和余弦函数y=cosx的最小正周期均为false,对false,false,可知false为该函数的周期,是否是最小正周期呢?我们继续探究:
false
可得:false也为函数f(x)=cos(sinx)的周期,但是否为该函数的最小正周期呢?我们来研究函数f(x)=cos(sinx)在区间false上的单调性,在区间false上,余弦函数y=cosx单调递减,正弦函数false在false上单调递增,在false上单调递减,故我们需要分这两个区间来讨论:
当false时,设false,因正弦函数y=sinx在false上单调递增,故false,令false,可得false,而在区间false上,
而在区间false上,余弦函数y=cosx单调递减,故:false即:false,从而,false时,函数f(x)=cos(sinx)单调递减。
同理可证,false时,函数f(x)=cos(sinx)单调递增
可得,函数f(x)=cos(sinx)在false上单调递减,在false上单调递增
结合false
可以确定:f(x)=cos(sinx)的最小正周期为false
这样,我们可以求出该函数的值域了:
显然:false,而false
故f(x)=cos(sinx)的值域为[cos1,1]
定义函数f(x)=sin(cosx)为“余正弦”函数,根据阅读材料的内容,解决下列问题:
(1)求该函数的定义域;
(2)判断该函数的奇偶性
(3)探究该函数的单调性及最小正周期,并求其值域。
高一数学
注意事项:
1.本试卷满分100分,考试时间90分钟
2.试卷共10页,其中试题卷6页,答题卷4页,答题前请沿裁切线裁切
3.考试过程中不得使用计算器
一、选择题(本大题共10小题,每小题4分,共40分,每小题有四个选项,其中只有一个选项正确,请将你认为正确的选项填在答题卷的相应位置上。)
1、已知集合false,则false( )
A.false B.false C、false D、false
2、圆心角弧度数和半径均为2的扇形的弧长为( )
A.1 B、2 C、4 D、8
3、已知向量false,且false是共线向量,则实数false的值为( )
A.-4 B、false C、false D.0
4、化简false ( )
A、false B、false C、false D、false
5、设函数false,则f(10)=( )
A.0 B.false C.1 D、false
6、设false为锐角,且false,则false ( )
A.false B.false C.false D、1
7.下列函数中,既是偶函数,又在区间false上单调递增的是( )
A、false B、false C、false D.false
8、函数false的定义域是( )
A.(1,+∞) B、(2,+∞) C、false D、false
9、设false,则a,b,c大小的关系为( )
A. a
A.false的最小值为false
B.false在区间false上单调递增
C.函数false的图像可由函数false的图像先向左平移false个单位,再将横坐标缩短为原来的一半(纵坐标不变)而得到
D.将函数y=f(x)的图像向左平移false个单位,所得函数的图像关于y轴对称
二、填空题(本大题共5小题,每小题4分,共20分。请将你认为正确的答案填在答题卷的相应位置上。)
11、若点false在幂函数false的图像上,则false
12计算false
13.设非零向量false满足false,则false与false的夹角为
14.false
false
15.以下条件
①a>b>1;②b>a>1
③1>a>b>0;④1>b>a>0
⑤a>1,1>b>0;⑥b>1,1>a>0
能够使得:false成立的有
三、解答题(本大题共4小题,每小题8分,共32分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分8分)
在平面直角坐标系中,已知角false的顶点都在坐标原点,始边都与x轴非负半轴重合,角false的终边上有一点A,坐标为(1,-1)
(1)求false的值;
(2)若角false满足下列三个条件之一
①锐角满足false
②锐角false的终边在直线false上;
③角false的终边与false的终边相同
请从上述三个条件中任选一个,你的选择是 ,求false的值。
17.(本小题满分8分)
设函数false为定义在R上的偶函数,当x≥0时,false。
(1)求函数false的解析式,并作出函数false的大致图象;
(2)判断函数false的零点个数(可结合图像判断)。
18、(本小题满分8分)
三角形ABC中,D为BC上一点,BD=2DC,设false,可以用false来表示出false,方法如下:
方法一:false
false
false
方法二:false
false
false
方法三:如图所示,过点D作AC的平行线交AB于点E,过点D作AB的平行线交AC于点F,则四边形AEDF为平行四边形
∵DF∥AB且BD=2DC,
false,false
∵ED∥AC,BD=2DC,
false
请参照上述方法之一(用其他方法也可),解决下列问题:
(1)三角形ABC中,D为BC的中点,设false,试用false表示false
(2)设D为直线BC上任意一点(除B、C两点),false,点A为直线BC外任意一点,false,证明:存在唯一实数对x,使得:false,且false。
19.(本题满分8分)
某市为了方便市民出行,解交通压力,引进甲、乙两家电动自行车营运商,在市定路段投放大量电动自行车供市民出行选择使用,两家收费标准分别如下:
甲:每骑行一次,需交基本使用费2元,骑行时间不超过40分钟的,每分钟收费0.05元,超出40分钟的,超出部分按每分钟0.055元收费。(如:某人骑行1小时,则其应付费用为:2+40×0.05+(60—40)×0.055=5.1元)
乙:不收取基本费,按实际骑行时间收费,每分钟收费0.08元
(1)写出选择骑行营运商甲的电动自行车的收费y与骑行时间(单位:分钟)的函数解析式;
(2)若某市民骑行营运商甲的电动自行车一次,花费7.3元,求该市民骑行的时间;
(3)该市民的骑行时间满足何条件时,选择甲营运商比乙营运商更划算。
四、阅读与探究(本大题1个小题,共8分。解答应写出文字说明,条理清晰。)
20.(本小题满分8分)
定义函数false为“正余弦”函数。结合学过的相关知识,我们可以得到该函数的性质。
1、我们知道,正弦函数y=sinx和余弦函数y=cosx的定义域均为R,故函数f(x)=cos(sinx)的定义域为R
2、我们知道,正弦函数y=sinx为奇函数,余弦函数y=cosx为偶函数,对f(x)=cos(sinx), false,可得:函数f(x)=cos(sinx)为偶函数
3、我们知道,正弦函数y=sinx和余弦函数y=cosx的最小正周期均为false,对false,false,可知false为该函数的周期,是否是最小正周期呢?我们继续探究:
false
可得:false也为函数f(x)=cos(sinx)的周期,但是否为该函数的最小正周期呢?我们来研究函数f(x)=cos(sinx)在区间false上的单调性,在区间false上,余弦函数y=cosx单调递减,正弦函数false在false上单调递增,在false上单调递减,故我们需要分这两个区间来讨论:
当false时,设false,因正弦函数y=sinx在false上单调递增,故false,令false,可得false,而在区间false上,
而在区间false上,余弦函数y=cosx单调递减,故:false即:false,从而,false时,函数f(x)=cos(sinx)单调递减。
同理可证,false时,函数f(x)=cos(sinx)单调递增
可得,函数f(x)=cos(sinx)在false上单调递减,在false上单调递增
结合false
可以确定:f(x)=cos(sinx)的最小正周期为false
这样,我们可以求出该函数的值域了:
显然:false,而false
故f(x)=cos(sinx)的值域为[cos1,1]
定义函数f(x)=sin(cosx)为“余正弦”函数,根据阅读材料的内容,解决下列问题:
(1)求该函数的定义域;
(2)判断该函数的奇偶性
(3)探究该函数的单调性及最小正周期,并求其值域。
同课章节目录
