第二十九章 投影与视图综合素质培优提升卷(含答案)
文档属性
| 名称 | 第二十九章 投影与视图综合素质培优提升卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下册
第二十九章
综合素质培优提升卷
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,箭头表示投影的方向,则图中圆柱体的投影是
( )
A.圆 B.矩形
C.梯形
D.圆柱
2.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是
( )
3.如图,下列选项中不是正六棱柱三视图的是
( )
4.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )
5.如图,它需再添一个面,折叠后才能围成一个正方体,右图中的黑色小正方形分别由四位同学补画,其中正确的是
( )
6.下图为某个几何体的三视图,则该几何体是
( )
7.长方体的主视图与俯视图如图,则这个长方体的体积是( )
A.52 B.32 C.24 D.9
第7题图
8.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有( )
A.9箱
B.10箱
C.11箱
D.12箱
第8题图
9.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是
( )
10.如图(1)、(2)、(3)、(4)是一天中四个不同时该的木杆在地面上的影子,将它们按时间先后顺序排列正确的一项是( )
A.(4)、(3)、(1)、(2)
B.(1)、(2)、(3)、(4)
C.(2)、(3)、(1)、(4)
D.(3)、(1)、(4)、(2)
二、填空题(每小题3分,共24分)
11.有下列投影:①阳光下遮阳伞的影子;②探照灯光下小明的读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子,其中属于平行投影的是
.(填序号)
12.对于如图所示的长方体(单位:mm),其左视图的面积比俯视图的面积
大
mm2.
第12题图
13.某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为
.
第13题图
14.一个几何体的三视图如图所示,其中主视图和俯视图都是矩形,则它的表面积是
.
第14题图
如图,为了测量学校旗杆的高度,小东用长为3.2
m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8
m,与旗杆相距22
m,则旗杆的高为
.
第15题图
16.如图,是由一些小立方块所搭成几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭与一个大正方体,至少还需要
个小立方块.
第16题图
17.如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为
.
第17题图
18.如图,是由8个相同的小立方块搭成的几何体,它的三视图都是2×2的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方体,则最多能拿掉小立方块的个数为
.
第18题图
三、解答题(共66分)
19.(10分)如图为某体育馆内的领奖台,请画出该立体图形的三视图.
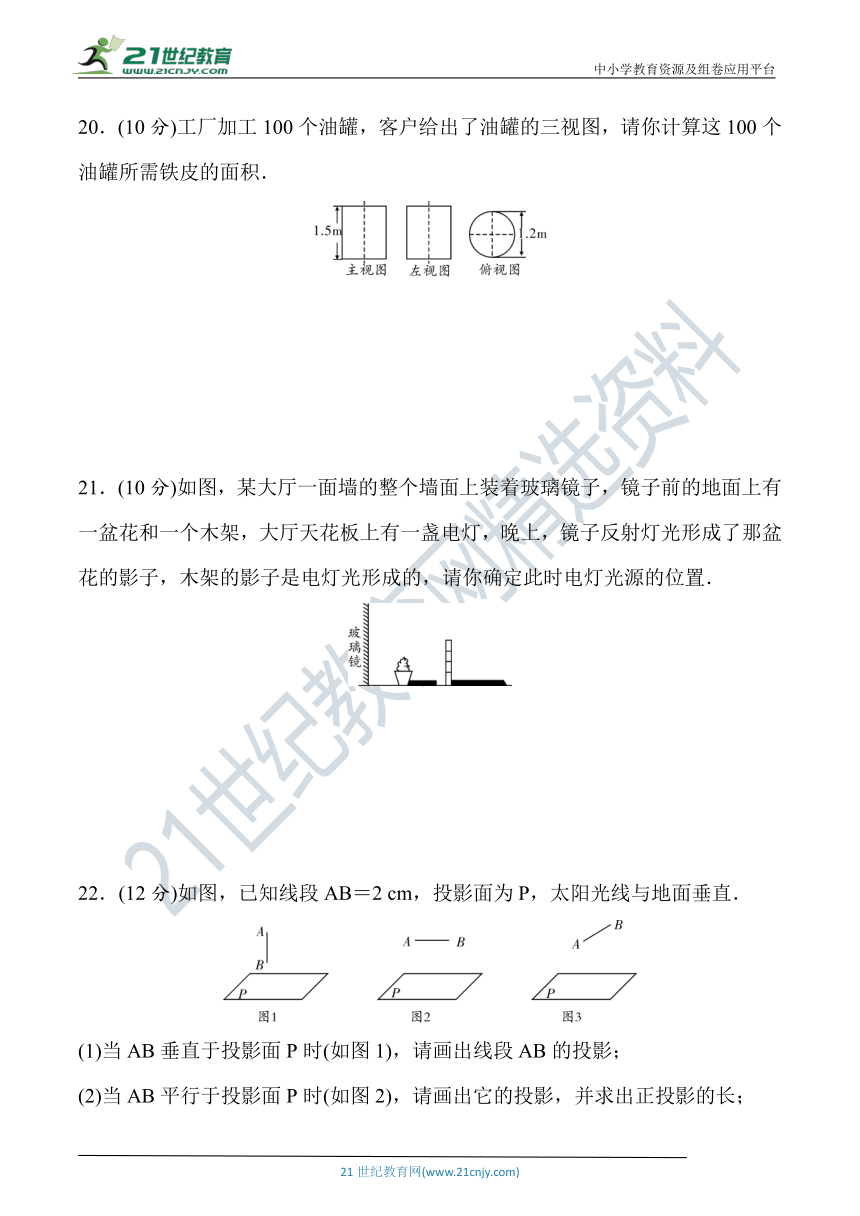
20.(10分)工厂加工100个油罐,客户给出了油罐的三视图,请你计算这100个油罐所需铁皮的面积.
21.(10分)如图,某大厅一面墙的整个墙面上装着玻璃镜子,镜子前的地面上有一盆花和一个木架,大厅天花板上有一盏电灯,晚上,镜子反射灯光形成了那盆花的影子,木架的影子是电灯光形成的,请你确定此时电灯光源的位置.
22.(12分)如图,已知线段AB=2
cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.
23.(12分)一个礼品包装盒的三视图如下,画出它的展开图,并计算它的表面积.
24.(12分)图①是一个三棱柱包装盒,它的底面是边长为10
cm的正三角形,三个侧面都是矩形.现将宽为15
cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算裁剪的角度∠BAD;
(2)计算按图③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
参考答案
一、选择题(每小题3分,共30分)
1.如图,箭头表示投影的方向,则图中圆柱体的投影是
( B )
A.圆 B.矩形
C.梯形
D.圆柱
2.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是
( D )
3.如图,下列选项中不是正六棱柱三视图的是
( B )
4.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( A )
5.如图,它需再添一个面,折叠后才能围成一个正方体,右图中的黑色小正方形分别由四位同学补画,其中正确的是
( C )
6.下图为某个几何体的三视图,则该几何体是
( D )
7.长方体的主视图与俯视图如图,则这个长方体的体积是( C )
A.52 B.32 C.24 D.9
第7题图
8.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有( A )
A.9箱
B.10箱
C.11箱
D.12箱
第8题图
9.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是
( B )
10.如图(1)、(2)、(3)、(4)是一天中四个不同时该的木杆在地面上的影子,将它们按时间先后顺序排列正确的一项是
( A )
A.(4)、(3)、(1)、(2)
B.(1)、(2)、(3)、(4)
C.(2)、(3)、(1)、(4)
D.(3)、(1)、(4)、(2)
二、填空题(每小题3分,共24分)
11.有下列投影:①阳光下遮阳伞的影子;②探照灯光下小明的读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子,其中属于平行投影的是__①②③④__.(填序号)
12.对于如图所示的长方体(单位:mm),其左视图的面积比俯视图的面积大__3__mm2.
第12题图
13.某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为__3π__.
第13题图
14.一个几何体的三视图如图所示,其中主视图和俯视图都是矩形,则它的表面积是__108__.
第14题图
如图,为了测量学校旗杆的高度,小东用长为3.2
m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8
m,与旗杆相距22
m,则旗杆的高为__12__m.
第15题图
16.如图,是由一些小立方块所搭成几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭与一个大正方体,至少还需要__54__个小立方块.
第16题图
17.如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为__3.24_m2__.
第17题图
18.如图,是由8个相同的小立方块搭成的几何体,它的三视图都是2×2的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方体,则最多能拿掉小立方块的个数为__2__.
第18题图
三、解答题(共66分)
19.(10分)如图为某体育馆内的领奖台,请画出该立体图形的三视图.
解:
20.(10分)工厂加工100个油罐,客户给出了油罐的三视图,请你计算这100个油罐所需铁皮的面积.
解:制作一个油罐所需铁皮的面积是
S=1.5×1.2π+2×
0.62×π=2.52π(m2).
所以制100个油罐需铁皮252πm2.
21.(10分)如图,某大厅一面墙的整个墙面上装着玻璃镜子,镜子前的地面上有一盆花和一个木架,大厅天花板上有一盏电灯,晚上,镜子反射灯光形成了那盆花的影子,木架的影子是电灯光形成的,请你确定此时电灯光源的位置.
解:设盆花顶点A与其影子的端点B的连线交镜面于点C,
过点C作镜面的垂线CM,作∠MCD=∠MCB,
(CD与CB位于CM两侧)木架顶点与其影子端点连线与CD的交点是电灯光源的位置.
22.(12分)如图,已知线段AB=2
cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.
解:(1)画图略.
画图略.AB的投影长2
cm.
(3)画图略,AB的正投影长
cm.
23.(12分)一个礼品包装盒的三视图如下,画出它的展开图,并计算它的表面积.
解:画图略,由三视图可知这个礼品盒为正六棱柱,
表面积为30×40×6+×30×30sin
60°×6×2=7
200+2
700.
24.(12分)图①是一个三棱柱包装盒,它的底面是边长为10
cm的正三角形,三个侧面都是矩形.现将宽为15
cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算裁剪的角度∠BAD;
(2)计算按图③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
解:(1)由题图②的包贴方法知:AB的长等于三棱住的侧边周长,
∴AB=30
cm.∵纸带宽为15
cm,
∴sin
∠DAB=sin
∠ABM===,
∴∠DAB=30°.
(2)在题图③中,将三棱柱沿过点A的侧棱剪开,
得到如图(1)的侧面展开图,
将图(1)中的△ABE向左平移30
cm,
△CDF向右平移30
cm,
拼成如图(2)中的?NAMC,
此平行四边形即为题图②中的?ABCD.
在图(2)中作CG⊥AM于点G,根据题意,在Rt△NBC中,
NC==40
(cm).在Rt△MCG中,
MG=MC·cos
30°=15
(cm),
∴所需矩形纸带的长为NC+MG=40+15=55(cm).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版九年级数学下册
第二十九章
综合素质培优提升卷
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,箭头表示投影的方向,则图中圆柱体的投影是
( )
A.圆 B.矩形
C.梯形
D.圆柱
2.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是
( )
3.如图,下列选项中不是正六棱柱三视图的是
( )
4.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( )
5.如图,它需再添一个面,折叠后才能围成一个正方体,右图中的黑色小正方形分别由四位同学补画,其中正确的是
( )
6.下图为某个几何体的三视图,则该几何体是
( )
7.长方体的主视图与俯视图如图,则这个长方体的体积是( )
A.52 B.32 C.24 D.9
第7题图
8.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有( )
A.9箱
B.10箱
C.11箱
D.12箱
第8题图
9.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是
( )
10.如图(1)、(2)、(3)、(4)是一天中四个不同时该的木杆在地面上的影子,将它们按时间先后顺序排列正确的一项是( )
A.(4)、(3)、(1)、(2)
B.(1)、(2)、(3)、(4)
C.(2)、(3)、(1)、(4)
D.(3)、(1)、(4)、(2)
二、填空题(每小题3分,共24分)
11.有下列投影:①阳光下遮阳伞的影子;②探照灯光下小明的读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子,其中属于平行投影的是
.(填序号)
12.对于如图所示的长方体(单位:mm),其左视图的面积比俯视图的面积
大
mm2.
第12题图
13.某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为
.
第13题图
14.一个几何体的三视图如图所示,其中主视图和俯视图都是矩形,则它的表面积是
.
第14题图
如图,为了测量学校旗杆的高度,小东用长为3.2
m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8
m,与旗杆相距22
m,则旗杆的高为
.
第15题图
16.如图,是由一些小立方块所搭成几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭与一个大正方体,至少还需要
个小立方块.
第16题图
17.如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为
.
第17题图
18.如图,是由8个相同的小立方块搭成的几何体,它的三视图都是2×2的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方体,则最多能拿掉小立方块的个数为
.
第18题图
三、解答题(共66分)
19.(10分)如图为某体育馆内的领奖台,请画出该立体图形的三视图.
20.(10分)工厂加工100个油罐,客户给出了油罐的三视图,请你计算这100个油罐所需铁皮的面积.
21.(10分)如图,某大厅一面墙的整个墙面上装着玻璃镜子,镜子前的地面上有一盆花和一个木架,大厅天花板上有一盏电灯,晚上,镜子反射灯光形成了那盆花的影子,木架的影子是电灯光形成的,请你确定此时电灯光源的位置.
22.(12分)如图,已知线段AB=2
cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.
23.(12分)一个礼品包装盒的三视图如下,画出它的展开图,并计算它的表面积.
24.(12分)图①是一个三棱柱包装盒,它的底面是边长为10
cm的正三角形,三个侧面都是矩形.现将宽为15
cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算裁剪的角度∠BAD;
(2)计算按图③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
参考答案
一、选择题(每小题3分,共30分)
1.如图,箭头表示投影的方向,则图中圆柱体的投影是
( B )
A.圆 B.矩形
C.梯形
D.圆柱
2.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是
( D )
3.如图,下列选项中不是正六棱柱三视图的是
( B )
4.如图所示的主视图、左视图、俯视图是下列哪个物体的三视图( A )
5.如图,它需再添一个面,折叠后才能围成一个正方体,右图中的黑色小正方形分别由四位同学补画,其中正确的是
( C )
6.下图为某个几何体的三视图,则该几何体是
( D )
7.长方体的主视图与俯视图如图,则这个长方体的体积是( C )
A.52 B.32 C.24 D.9
第7题图
8.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有( A )
A.9箱
B.10箱
C.11箱
D.12箱
第8题图
9.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是
( B )
10.如图(1)、(2)、(3)、(4)是一天中四个不同时该的木杆在地面上的影子,将它们按时间先后顺序排列正确的一项是
( A )
A.(4)、(3)、(1)、(2)
B.(1)、(2)、(3)、(4)
C.(2)、(3)、(1)、(4)
D.(3)、(1)、(4)、(2)
二、填空题(每小题3分,共24分)
11.有下列投影:①阳光下遮阳伞的影子;②探照灯光下小明的读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子,其中属于平行投影的是__①②③④__.(填序号)
12.对于如图所示的长方体(单位:mm),其左视图的面积比俯视图的面积大__3__mm2.
第12题图
13.某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为__3π__.
第13题图
14.一个几何体的三视图如图所示,其中主视图和俯视图都是矩形,则它的表面积是__108__.
第14题图
如图,为了测量学校旗杆的高度,小东用长为3.2
m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8
m,与旗杆相距22
m,则旗杆的高为__12__m.
第15题图
16.如图,是由一些小立方块所搭成几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭与一个大正方体,至少还需要__54__个小立方块.
第16题图
17.如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为__3.24_m2__.
第17题图
18.如图,是由8个相同的小立方块搭成的几何体,它的三视图都是2×2的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方体,则最多能拿掉小立方块的个数为__2__.
第18题图
三、解答题(共66分)
19.(10分)如图为某体育馆内的领奖台,请画出该立体图形的三视图.
解:
20.(10分)工厂加工100个油罐,客户给出了油罐的三视图,请你计算这100个油罐所需铁皮的面积.
解:制作一个油罐所需铁皮的面积是
S=1.5×1.2π+2×
0.62×π=2.52π(m2).
所以制100个油罐需铁皮252πm2.
21.(10分)如图,某大厅一面墙的整个墙面上装着玻璃镜子,镜子前的地面上有一盆花和一个木架,大厅天花板上有一盏电灯,晚上,镜子反射灯光形成了那盆花的影子,木架的影子是电灯光形成的,请你确定此时电灯光源的位置.
解:设盆花顶点A与其影子的端点B的连线交镜面于点C,
过点C作镜面的垂线CM,作∠MCD=∠MCB,
(CD与CB位于CM两侧)木架顶点与其影子端点连线与CD的交点是电灯光源的位置.
22.(12分)如图,已知线段AB=2
cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.
解:(1)画图略.
画图略.AB的投影长2
cm.
(3)画图略,AB的正投影长
cm.
23.(12分)一个礼品包装盒的三视图如下,画出它的展开图,并计算它的表面积.
解:画图略,由三视图可知这个礼品盒为正六棱柱,
表面积为30×40×6+×30×30sin
60°×6×2=7
200+2
700.
24.(12分)图①是一个三棱柱包装盒,它的底面是边长为10
cm的正三角形,三个侧面都是矩形.现将宽为15
cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算裁剪的角度∠BAD;
(2)计算按图③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
解:(1)由题图②的包贴方法知:AB的长等于三棱住的侧边周长,
∴AB=30
cm.∵纸带宽为15
cm,
∴sin
∠DAB=sin
∠ABM===,
∴∠DAB=30°.
(2)在题图③中,将三棱柱沿过点A的侧棱剪开,
得到如图(1)的侧面展开图,
将图(1)中的△ABE向左平移30
cm,
△CDF向右平移30
cm,
拼成如图(2)中的?NAMC,
此平行四边形即为题图②中的?ABCD.
在图(2)中作CG⊥AM于点G,根据题意,在Rt△NBC中,
NC==40
(cm).在Rt△MCG中,
MG=MC·cos
30°=15
(cm),
∴所需矩形纸带的长为NC+MG=40+15=55(cm).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
