新人教版数学 七年级上 4.3.1-4.3.3角
文档属性
| 名称 | 新人教版数学 七年级上 4.3.1-4.3.3角 |

|
|
| 格式 | rar | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-18 00:00:00 | ||
图片预览







文档简介
(共44张PPT)
问题:
时钟的时针与分针,棱锥相交的两条棱,都给我们什么样的平面图形的形象?请把它画出来.
1.角的概念.
(1)提出问题:从上面问题中,你能发现这些图形有什么共同点吗?
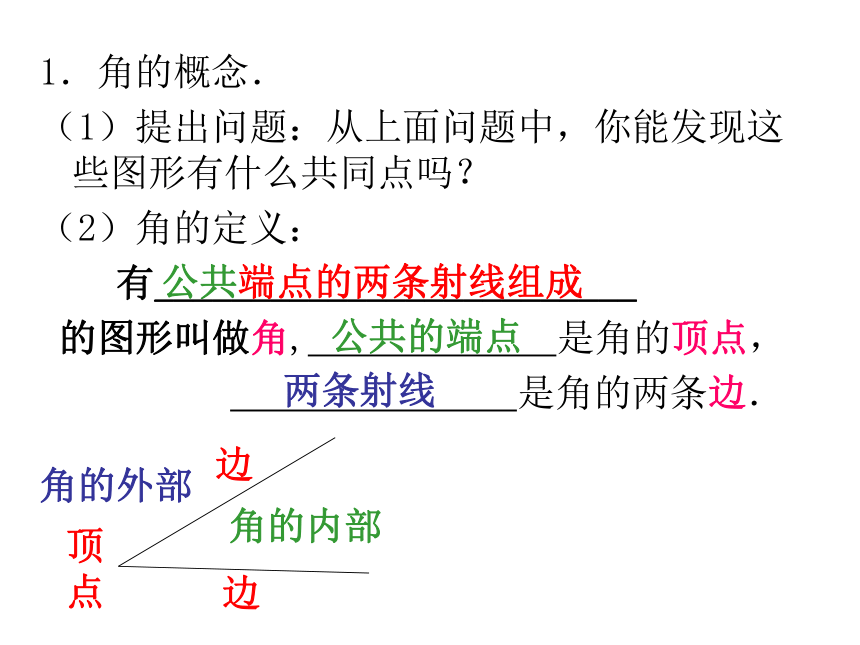
(2)角的定义:
有_________________________
的图形叫做角, 是角的顶点,
是角的两条边.
边
边
顶点
角的内部
角的外部
公共端点的两条射线组成
公共的端点
两条射线
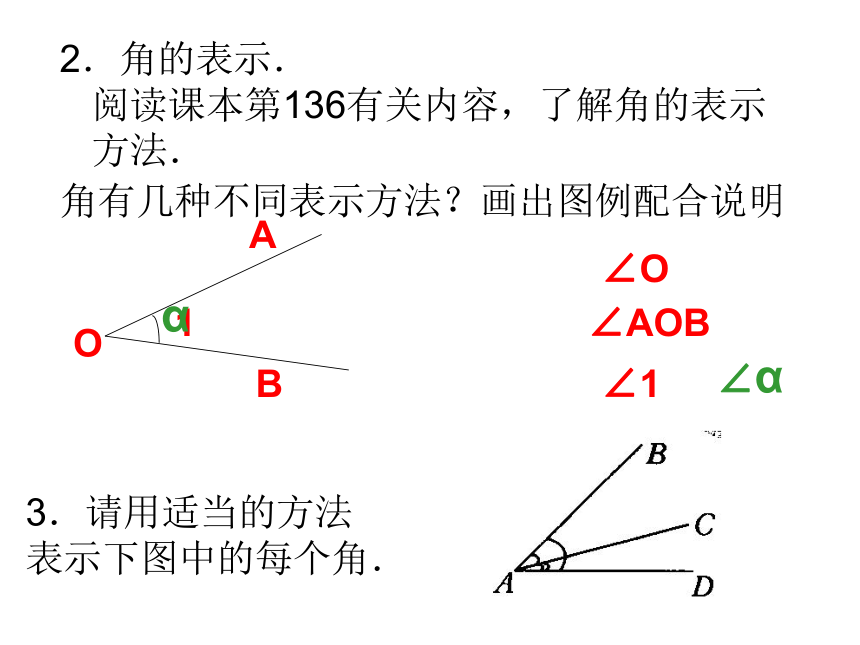
角有几种不同表示方法?画出图例配合说明
3.请用适当的方法
表示下图中的每个角.
2.角的表示.
阅读课本第136有关内容,了解角的表示
方法.
O
A
B
∠O
∠AOB
∠1
1
α
∠α
4.阅读课本第136页思考题,进行小组交流,再回答:
角也可以看作 .
当角的两边满足 条件时,它是平角。
当角的两边满足 条件时,它是周角。
由一条射线绕着它的端点旋转
而形成的图形
形成一条直线
重合
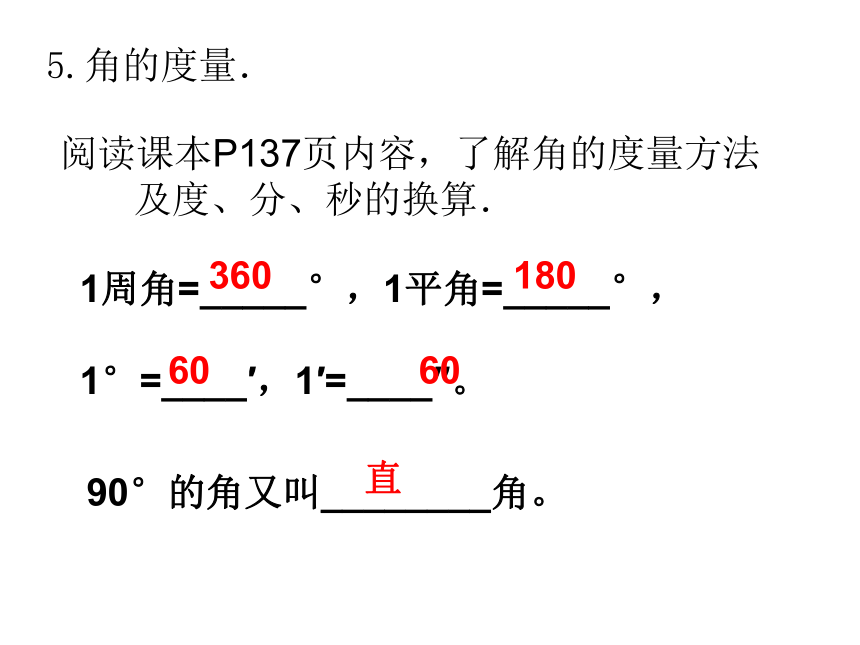
5.角的度量.
阅读课本P137页内容,了解角的度量方法
及度、分、秒的换算.
1周角=_____°,1平角=_____°,
1°=____′,1′=____″。
90°的角又叫________角。
360
180
60
60
直
例:把一个周角7等分,每一份是多少度的角(精确到分)?
7.度分秒的互化
⑴ 57.32 = 度 分 秒,
⑵ 17°6′36″= 度。
⑶ 14°25′12″= 度。
⑷ 28°39′+ 61°35′=___________ ;
⑸ 54°23′- 36°31′=____________
⑹ =___________
57
19
12
17.11
14.42
课本第138页练习1、2、3.
拓展训练
1.请问时针、分针、秒针分别转多长时间得 到一个周角?一个平角?
想一想:时钟在5点15分时,时钟的时针与分针
所成的角是多少度?
五点多少分,钟表上的时针与分针成直角、平角?
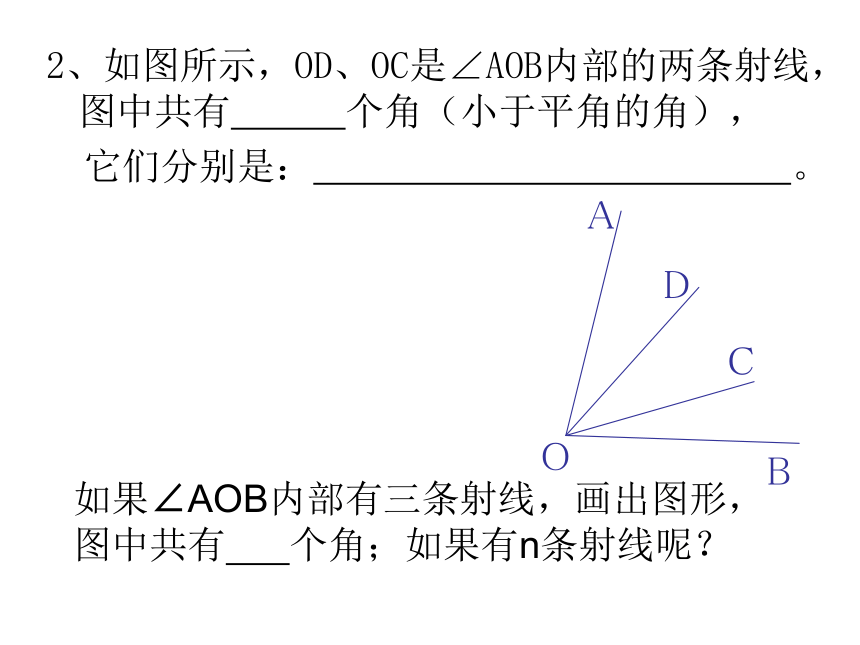
2、如图所示,OD、OC是∠AOB内部的两条射线,图中共有 个角(小于平角的角),
它们分别是: 。
如果∠AOB内部有三条射线,画出图形,
图中共有 个角;如果有n条射线呢?
1、回顾怎样比较两条线段的大小?
2、什么叫角?如何来表示与度量它?
3、在一块三角板中,你能说出它们的大小吗?
你会画75°的角吗?
二、探究新知(阅读课本138页)
(一)角的比较与角的和差
1、与线段长短的比较相类似,
比较两个角的大小有2种方法:
方法一为:_________________________;
方法二为:____________________________
通过度量
将角的一边重合,比较另外一边位置
比较图中的∠AOB与∠A’O’B’的大小。
A’
B
'
(B)
A
O
(1)图中共有几个角?分别是 。
2、如图
(2)比较大小: ∠AOB ∠AOC
∠AOD ∠COB
(3)填空:∠AOD= _______+_________;
∠BOC=______ - ______
(4)如果∠BOD=∠AOC,
那么图中还有相同的角吗?
<
>
∠AOC
∠DOC
∠AOC
∠AOB
∠AOB=∠COD
(二)、角的平分线及角的倍分
1、如右图,如果∠AOC=∠BOC,那么
∠AOB= 2 ______= 2 _______;
∠AOC=∠BOC =________.
2、我们称射线OC是∠AOB的角平分线,
也可以说射线OC平分∠AOB。
角平分线的定义:
______________________________
∠AOC
∠BOC
∠AOB
从角的顶点出发,将这个角分成相等两个的角的射线称为这个角的平分线
3、怎样画个角的角平分线?画出上图1、2中的角平分线。
4、如果在图中 ∠AOB=∠BOC =∠COD,那么OB、OC就叫∠AOD的_________;
OB、OC又分别是______、______的角平分线。
三等分线
∠AOC
∠BOD
三、应用举例
例:1)如图1,O是直线AB上一点,∠AOC=53°,OD平分∠BOC,求∠BOD的度数?
2)如图,O是直线AB上一点,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数?
四、自我检测
1、如下图,用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC;
(2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC;
(4)∠AOD______∠AOC+∠BOD.
=
>
=
<
2、如图1,∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,
⑴求∠MON的度数,
⑵若∠AOB=∠α,若∠BOC=∠β(∠β为锐角)
其他条件不变,求∠MON的度数。
(用含α、β的式子表示)
⑶探究:从⑴、⑵中你发现有什么规律?
(4)如图2,已知OM平分∠COB,ON平分∠AOC,试猜想∠MON的大小只与图中哪个角的大小有关,有怎样的关系?你能给出说明吗?
1、找出图中各角之间的和差关系,并用式子
表示出来.(如下图)
2、如果∠AOB=30°,∠COB=18°,
那么∠AOC=_________.
∠AOB+∠BOC=∠AOC
∠AOC -∠BOC= ∠AOB
48°
3、口述用三角板如何画75°、15°的角;用一副三角板你还可以画出哪些小于180°的角?
15°30°45°60°75°90°105°120°
135°150°165°
二、探究新知
1、如下图,已知∠1,∠2(∠1>∠2),画∠AOB,使它等于:
(1)2∠1-∠2; (2)(∠1+∠2).
2、如果∠1=78°19′40″,∠2=20°,那么∠1+∠2=_________,∠1-∠2=_________.
2∠1=___________; ∠1=_____________.
98°19′40″
58°19′40″
39°9′50″
156°39′20″
三、应用举例
例1、如图,O是直线AB上一点,∠AOD=43°19′,∠BOC=45°,
求∠COD、∠AOC的度数。
∠AOC=180°-45°=135°
∠DOC=∠AOC-∠AOD
=135°- 43°19′=91°41’
例2、计算:
(1)28°1′40″+53°59′20″
(2)68°-53°59′20″
(3)8°23′17″ 4
(4)90° 7
82°1′
14°40″
33°33′8″
12°51′26″
四、自我检测
1、课本P140—141页练习;课本P143页习题4.3中3、4、5、6.
2、如果∠1=∠2,∠1+∠3=90°,则∠2+∠3=_______.
3、如下图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
90°
设∠COD=x°则∠AOB=3x
∠COD+∠AOB= ∠BOD+∠AOC
4x=60°+90°=150°
x=37.5° 3x=112.5°
4、如下图,已知OB平分∠AOC,OD平分∠COE,∠AOC=80°,∠DOE=30°.
求(1)∠AOB,(2)∠COD,
(3)∠BOD.
五、拓展训练
1、如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=__ _.
34°
2、如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,求∠AOC的度数?
3、如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数
探索新知:
1、互为余角的定义:
如果两个角__________________,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
若∠1+∠2=90°,则∠1是∠2的余角或称∠2是∠1的余角。
的和是直角
2、互为补角的定义:
如果两个角_________________,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
若∠3+∠4=180°,则∠3是∠4的补角
或称∠4是∠3的补角
的和是平角
(3)填空:①70°的余角是 ,
补角是 。
62°23′的余角与补角分别是 。
②∠ (∠ <90°)的它的余角是 ,
它的补角是 。
结论:同一个锐角的补角比它的余角大 度。
20°
110°
27°37’
117°37’
90°- ∠
180°- ∠
90
5、探究补角(余角)的性质:
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?归纳结论。
补角性质:
根据补角的性质你能否归纳余角的性质?
余角性质:
同角或等角的补角相等。
同角或等角的余角相等。
三、应用举例
例1:若一个角的补角等于它的余角4倍,求这个角的度数。
例2:一个角的补角是它的3倍,这个角是多少度
解:设这个角是x°,则
180°-x
(90°- x)
4
=
四、自我检测
1、课本144页7、8、13
2、如图,∠AOB=90°,∠COD=∠EOD=90°,
C,O,E在一条直线上,且∠2=∠4,
请说出∠1与∠3之间的关系?并试着说明理由?
∠1与∠2是什么关系?图中有哪几对互余的角、哪几对互补的角
互余的角
∠1与∠2
∠1与∠4
∠3与∠2
∠3与∠4
互补的角
∠COD、∠EOD与∠AOB两两之间互补
∠1(或∠3)与∠AOE
∠2(或∠4)与∠BOC
共有7对互补的角!
3、如图,已知∠AOC =∠BOD=90°,指出图中相等的角、互余的角、互补的角。
∠AOD=∠BOC
∠DOC+∠BOC=90°
∠DOC+∠AOD=90°
∠AOC+∠BOD=180°
∠DOC+∠BOA=180°!
问题:
时钟的时针与分针,棱锥相交的两条棱,都给我们什么样的平面图形的形象?请把它画出来.
1.角的概念.
(1)提出问题:从上面问题中,你能发现这些图形有什么共同点吗?
(2)角的定义:
有_________________________
的图形叫做角, 是角的顶点,
是角的两条边.
边
边
顶点
角的内部
角的外部
公共端点的两条射线组成
公共的端点
两条射线
角有几种不同表示方法?画出图例配合说明
3.请用适当的方法
表示下图中的每个角.
2.角的表示.
阅读课本第136有关内容,了解角的表示
方法.
O
A
B
∠O
∠AOB
∠1
1
α
∠α
4.阅读课本第136页思考题,进行小组交流,再回答:
角也可以看作 .
当角的两边满足 条件时,它是平角。
当角的两边满足 条件时,它是周角。
由一条射线绕着它的端点旋转
而形成的图形
形成一条直线
重合
5.角的度量.
阅读课本P137页内容,了解角的度量方法
及度、分、秒的换算.
1周角=_____°,1平角=_____°,
1°=____′,1′=____″。
90°的角又叫________角。
360
180
60
60
直
例:把一个周角7等分,每一份是多少度的角(精确到分)?
7.度分秒的互化
⑴ 57.32 = 度 分 秒,
⑵ 17°6′36″= 度。
⑶ 14°25′12″= 度。
⑷ 28°39′+ 61°35′=___________ ;
⑸ 54°23′- 36°31′=____________
⑹ =___________
57
19
12
17.11
14.42
课本第138页练习1、2、3.
拓展训练
1.请问时针、分针、秒针分别转多长时间得 到一个周角?一个平角?
想一想:时钟在5点15分时,时钟的时针与分针
所成的角是多少度?
五点多少分,钟表上的时针与分针成直角、平角?
2、如图所示,OD、OC是∠AOB内部的两条射线,图中共有 个角(小于平角的角),
它们分别是: 。
如果∠AOB内部有三条射线,画出图形,
图中共有 个角;如果有n条射线呢?
1、回顾怎样比较两条线段的大小?
2、什么叫角?如何来表示与度量它?
3、在一块三角板中,你能说出它们的大小吗?
你会画75°的角吗?
二、探究新知(阅读课本138页)
(一)角的比较与角的和差
1、与线段长短的比较相类似,
比较两个角的大小有2种方法:
方法一为:_________________________;
方法二为:____________________________
通过度量
将角的一边重合,比较另外一边位置
比较图中的∠AOB与∠A’O’B’的大小。
A’
B
'
(B)
A
O
(1)图中共有几个角?分别是 。
2、如图
(2)比较大小: ∠AOB ∠AOC
∠AOD ∠COB
(3)填空:∠AOD= _______+_________;
∠BOC=______ - ______
(4)如果∠BOD=∠AOC,
那么图中还有相同的角吗?
<
>
∠AOC
∠DOC
∠AOC
∠AOB
∠AOB=∠COD
(二)、角的平分线及角的倍分
1、如右图,如果∠AOC=∠BOC,那么
∠AOB= 2 ______= 2 _______;
∠AOC=∠BOC =________.
2、我们称射线OC是∠AOB的角平分线,
也可以说射线OC平分∠AOB。
角平分线的定义:
______________________________
∠AOC
∠BOC
∠AOB
从角的顶点出发,将这个角分成相等两个的角的射线称为这个角的平分线
3、怎样画个角的角平分线?画出上图1、2中的角平分线。
4、如果在图中 ∠AOB=∠BOC =∠COD,那么OB、OC就叫∠AOD的_________;
OB、OC又分别是______、______的角平分线。
三等分线
∠AOC
∠BOD
三、应用举例
例:1)如图1,O是直线AB上一点,∠AOC=53°,OD平分∠BOC,求∠BOD的度数?
2)如图,O是直线AB上一点,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数?
四、自我检测
1、如下图,用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC;
(2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC;
(4)∠AOD______∠AOC+∠BOD.
=
>
=
<
2、如图1,∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,
⑴求∠MON的度数,
⑵若∠AOB=∠α,若∠BOC=∠β(∠β为锐角)
其他条件不变,求∠MON的度数。
(用含α、β的式子表示)
⑶探究:从⑴、⑵中你发现有什么规律?
(4)如图2,已知OM平分∠COB,ON平分∠AOC,试猜想∠MON的大小只与图中哪个角的大小有关,有怎样的关系?你能给出说明吗?
1、找出图中各角之间的和差关系,并用式子
表示出来.(如下图)
2、如果∠AOB=30°,∠COB=18°,
那么∠AOC=_________.
∠AOB+∠BOC=∠AOC
∠AOC -∠BOC= ∠AOB
48°
3、口述用三角板如何画75°、15°的角;用一副三角板你还可以画出哪些小于180°的角?
15°30°45°60°75°90°105°120°
135°150°165°
二、探究新知
1、如下图,已知∠1,∠2(∠1>∠2),画∠AOB,使它等于:
(1)2∠1-∠2; (2)(∠1+∠2).
2、如果∠1=78°19′40″,∠2=20°,那么∠1+∠2=_________,∠1-∠2=_________.
2∠1=___________; ∠1=_____________.
98°19′40″
58°19′40″
39°9′50″
156°39′20″
三、应用举例
例1、如图,O是直线AB上一点,∠AOD=43°19′,∠BOC=45°,
求∠COD、∠AOC的度数。
∠AOC=180°-45°=135°
∠DOC=∠AOC-∠AOD
=135°- 43°19′=91°41’
例2、计算:
(1)28°1′40″+53°59′20″
(2)68°-53°59′20″
(3)8°23′17″ 4
(4)90° 7
82°1′
14°40″
33°33′8″
12°51′26″
四、自我检测
1、课本P140—141页练习;课本P143页习题4.3中3、4、5、6.
2、如果∠1=∠2,∠1+∠3=90°,则∠2+∠3=_______.
3、如下图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
90°
设∠COD=x°则∠AOB=3x
∠COD+∠AOB= ∠BOD+∠AOC
4x=60°+90°=150°
x=37.5° 3x=112.5°
4、如下图,已知OB平分∠AOC,OD平分∠COE,∠AOC=80°,∠DOE=30°.
求(1)∠AOB,(2)∠COD,
(3)∠BOD.
五、拓展训练
1、如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=__ _.
34°
2、如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,求∠AOC的度数?
3、如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数
探索新知:
1、互为余角的定义:
如果两个角__________________,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
若∠1+∠2=90°,则∠1是∠2的余角或称∠2是∠1的余角。
的和是直角
2、互为补角的定义:
如果两个角_________________,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
若∠3+∠4=180°,则∠3是∠4的补角
或称∠4是∠3的补角
的和是平角
(3)填空:①70°的余角是 ,
补角是 。
62°23′的余角与补角分别是 。
②∠ (∠ <90°)的它的余角是 ,
它的补角是 。
结论:同一个锐角的补角比它的余角大 度。
20°
110°
27°37’
117°37’
90°- ∠
180°- ∠
90
5、探究补角(余角)的性质:
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?归纳结论。
补角性质:
根据补角的性质你能否归纳余角的性质?
余角性质:
同角或等角的补角相等。
同角或等角的余角相等。
三、应用举例
例1:若一个角的补角等于它的余角4倍,求这个角的度数。
例2:一个角的补角是它的3倍,这个角是多少度
解:设这个角是x°,则
180°-x
(90°- x)
4
=
四、自我检测
1、课本144页7、8、13
2、如图,∠AOB=90°,∠COD=∠EOD=90°,
C,O,E在一条直线上,且∠2=∠4,
请说出∠1与∠3之间的关系?并试着说明理由?
∠1与∠2是什么关系?图中有哪几对互余的角、哪几对互补的角
互余的角
∠1与∠2
∠1与∠4
∠3与∠2
∠3与∠4
互补的角
∠COD、∠EOD与∠AOB两两之间互补
∠1(或∠3)与∠AOE
∠2(或∠4)与∠BOC
共有7对互补的角!
3、如图,已知∠AOC =∠BOD=90°,指出图中相等的角、互余的角、互补的角。
∠AOD=∠BOC
∠DOC+∠BOC=90°
∠DOC+∠AOD=90°
∠AOC+∠BOD=180°
∠DOC+∠BOA=180°!
