2020-2021学年人教版八年级下册数学同步练习:18.2.1 矩形(Word版 无答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学同步练习:18.2.1 矩形(Word版 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览



文档简介
18.2.1
矩形
一、选择题
1、如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是(
)
A、AB=CD
B、AD=BC
C、∠AOB=45°
D、∠ABC=90°
矩形具有而平行四边形不具有的性质是(
)
A
、对角相等
B、对角线互相平分
C、一组对边平行另一组对边相等
D、对角线相等
如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为(
)
A、4
B、3
C、2
D、1
如图,在矩形ABCD中,若AC=2AB,则∠AOB的大小是(
)
30°
B、45°
C、60°
D、90°
在Rt△ABC中,∠C=90°,∠B=30°,最短边长为5cm,则最长边上的中线长是(
)。
5cm
B、15cm
C、10cm
D、2.5cm
数学课上,老师要同学们判断一个四边形门框是否为矩形。下面是某合作小组的4位同学拟定的方案,其中正确的是(
)
测量对角线是否互相平分
B、测量两组对边是否分别相等
C、测量一组对角是否都是直角
D、测量三个角是否都是直角
ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是(
)
A、AB=AD
B、OA=OB
C、AC=BD
D、DC⊥BC
如图,在Rt△ABC中,∠BAC=90°,D、E分别BC、AB的中点,且AC=6cm,AB=8cm,则△ADE的周长是(
)
10cm
B、12cm
C、14cm
D、16cm
如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C?处,BC?交AD于点E,则线段DE的长为(
)
A、3
B、
C、5
D、
若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是(
)
A、矩形
B、平行四边形
C、对角线互相垂直的四边形
D、对角线相等的四边形
11、如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为(
)
A、5
B、10
C、12
D、13
12、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为(
)
A、3
B、4
C、5
D、6
下列关于矩形的说法中正确的是(
)
对角线相等的四边形是矩形
B、矩形的对角线相等且互相平分
对角线互相平分的四边形是矩形
D、矩形的对角线互相垂直且平分
在平行四边形ABCD中,AB=3,BC=4,当平行四边形ABCD的面积最大时,下列结论正确的是(
)
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD
①②③
B、①②④
C、②③④
D、①③④
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB。添加一个条件,不能使四边形DBCE成为矩形的是(
)
AB=BE
B、BE⊥DC
C、∠ADB=90°
D、CE⊥DE
填空题
16、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点。若DE=5,则AB的长为
。
17、用一把刻度尺来判定一个零件是矩形的方法是先测量两组对边是否分别相等,然后测量两条对角线是否相等,这样做的依据是
。
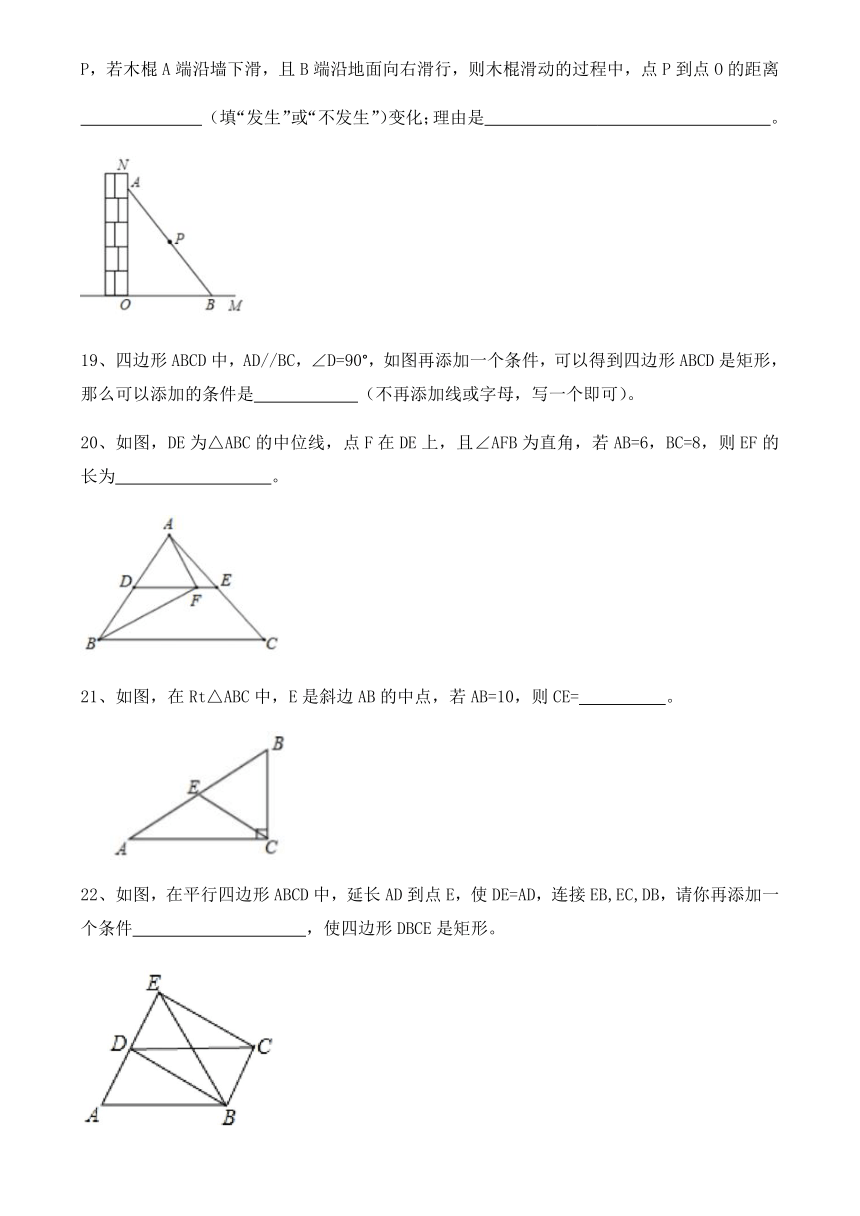
18、如图,一根长am的木棍(AB)斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行,则木棍滑动的过程中,点P到点O的距离
(填“发生”或“不发生”)变化;理由是
。
四边形ABCD中,AD//BC,∠D=90°,如图再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是
(不再添加线或字母,写一个即可)。
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=6,BC=8,则EF的长为
。
如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE=
。
如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你再添加一个条件
,使四边形DBCE是矩形。
解答题
如图,已知在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF,AD。
求证:EF=AD
已知,如图
ABCD的四个内角的平分线分别相交于点E、F、G、H。
求证:四边形EFGH是矩形。
如图,在矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,试说明BE=CF。
如图,在△ABC中,D是AB的中点,E是CD的中点,过点C作CF//AB交AE的延长线于点F,连接BF。
求证:DB=CF;
如果AC=BC,试判断四边形BDCF的形状,并证明你的结论。
已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交AB、AC于点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N。
求证:四边形AFBE是矩形;
求证:MN=.
如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E、F,连接BE、CF。
请你添加一个条件,使得,你添加的条件是
,并证明;
在问题(1)中,当BH与EH满足什么数量关系时,四边形BFCE是矩形?请说明理由。
已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF.
求证:BF=CD
矩形
一、选择题
1、如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是(
)
A、AB=CD
B、AD=BC
C、∠AOB=45°
D、∠ABC=90°
矩形具有而平行四边形不具有的性质是(
)
A
、对角相等
B、对角线互相平分
C、一组对边平行另一组对边相等
D、对角线相等
如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为(
)
A、4
B、3
C、2
D、1
如图,在矩形ABCD中,若AC=2AB,则∠AOB的大小是(
)
30°
B、45°
C、60°
D、90°
在Rt△ABC中,∠C=90°,∠B=30°,最短边长为5cm,则最长边上的中线长是(
)。
5cm
B、15cm
C、10cm
D、2.5cm
数学课上,老师要同学们判断一个四边形门框是否为矩形。下面是某合作小组的4位同学拟定的方案,其中正确的是(
)
测量对角线是否互相平分
B、测量两组对边是否分别相等
C、测量一组对角是否都是直角
D、测量三个角是否都是直角
ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是(
)
A、AB=AD
B、OA=OB
C、AC=BD
D、DC⊥BC
如图,在Rt△ABC中,∠BAC=90°,D、E分别BC、AB的中点,且AC=6cm,AB=8cm,则△ADE的周长是(
)
10cm
B、12cm
C、14cm
D、16cm
如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C?处,BC?交AD于点E,则线段DE的长为(
)
A、3
B、
C、5
D、
若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是(
)
A、矩形
B、平行四边形
C、对角线互相垂直的四边形
D、对角线相等的四边形
11、如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为(
)
A、5
B、10
C、12
D、13
12、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为(
)
A、3
B、4
C、5
D、6
下列关于矩形的说法中正确的是(
)
对角线相等的四边形是矩形
B、矩形的对角线相等且互相平分
对角线互相平分的四边形是矩形
D、矩形的对角线互相垂直且平分
在平行四边形ABCD中,AB=3,BC=4,当平行四边形ABCD的面积最大时,下列结论正确的是(
)
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD
①②③
B、①②④
C、②③④
D、①③④
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB。添加一个条件,不能使四边形DBCE成为矩形的是(
)
AB=BE
B、BE⊥DC
C、∠ADB=90°
D、CE⊥DE
填空题
16、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点。若DE=5,则AB的长为
。
17、用一把刻度尺来判定一个零件是矩形的方法是先测量两组对边是否分别相等,然后测量两条对角线是否相等,这样做的依据是
。
18、如图,一根长am的木棍(AB)斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行,则木棍滑动的过程中,点P到点O的距离
(填“发生”或“不发生”)变化;理由是
。
四边形ABCD中,AD//BC,∠D=90°,如图再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是
(不再添加线或字母,写一个即可)。
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=6,BC=8,则EF的长为
。
如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE=
。
如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你再添加一个条件
,使四边形DBCE是矩形。
解答题
如图,已知在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF,AD。
求证:EF=AD
已知,如图
ABCD的四个内角的平分线分别相交于点E、F、G、H。
求证:四边形EFGH是矩形。
如图,在矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,试说明BE=CF。
如图,在△ABC中,D是AB的中点,E是CD的中点,过点C作CF//AB交AE的延长线于点F,连接BF。
求证:DB=CF;
如果AC=BC,试判断四边形BDCF的形状,并证明你的结论。
已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交AB、AC于点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N。
求证:四边形AFBE是矩形;
求证:MN=.
如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E、F,连接BE、CF。
请你添加一个条件,使得,你添加的条件是
,并证明;
在问题(1)中,当BH与EH满足什么数量关系时,四边形BFCE是矩形?请说明理由。
已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF.
求证:BF=CD
