山东省烟台市莱州市2020——2021学年七年级上学期期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 山东省烟台市莱州市2020——2021学年七年级上学期期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 13:32:18 | ||
图片预览



文档简介
2020-2021学年山东省烟台市莱州市七年级(上)期中数学试卷(五四学制)
一、选择题(本题共10个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,请将正确答案的标号填在下表中)
1.下列图案中,有且只有三条对称轴的是( )
A. B. C. D.
2.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
3.下列各组数据能组成直角三角形的是( )
A.2,3,4 B.4,5,6 C.8,15,17 D.11,12,13
4.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是( )
A.30°、60° B.40°、70° C.50°、60° D.100°、30°
5.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
6.对于下列命题:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
7.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.42或37
8.如图,四边形ABCD是轴对称图形,直线AC是对称轴.如果∠BAD+∠BCD=170°,那么∠B等于( )
A.80° B.85° C.95° D.105°
9.如图,△ABC的三边AB、BC、CA长分别是10、15、20.其三条角平分线交于点O,将△ABC分为三个三角形,S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
10.如图,一架云梯25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
A.4米 B.6米 C.8米 D.10米
二、填空题(本题共10个小题)
11.正五角星形共有 条对称轴.
12.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以 个三角形.
13.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为 .
14.一帆船由于风向先向正西航行80千米,然后向正南航行150千米,这时它离出发点有 千米.
15.等腰三角形的两边长分别是6cm和4cm,那么第三边的长为 .
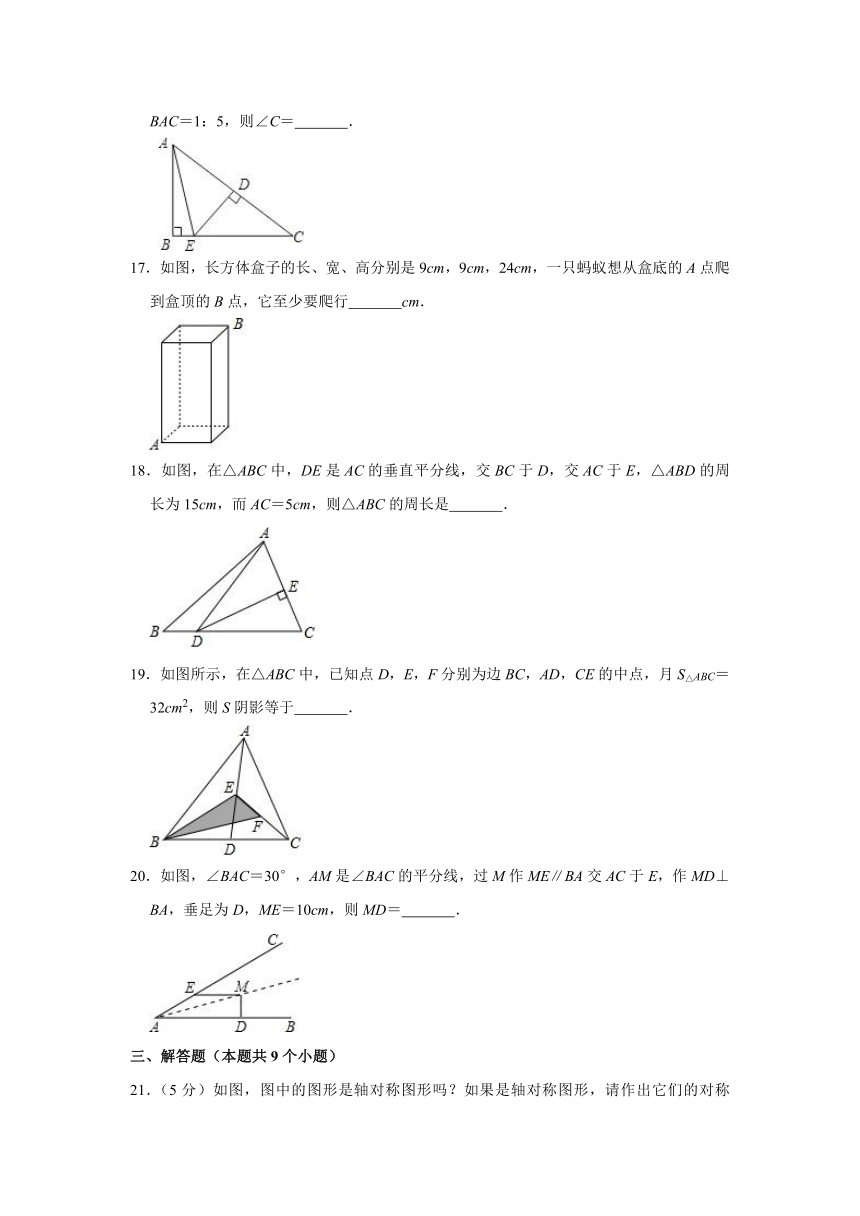
16.如图,在Rt△ABC中,B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C= .
17.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 cm.
18.如图,在△ABC中,DE是AC的垂直平分线,交BC于D,交AC于E,△ABD的周长为15cm,而AC=5cm,则△ABC的周长是 .
19.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,月S△ABC=32cm2,则S阴影等于 .
20.如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD= .
三、解答题(本题共9个小题)
21.(5分)如图,图中的图形是轴对称图形吗?如果是轴对称图形,请作出它们的对称轴.
22.(5分)如图,已知线段a、c和m,求作:△ABC,使BC=a,AB=c,BC边上的中线AM=m.
要求:不写作法,保留作图痕迹,标注字母.
23.(5分)如图,一菜农要修建蔬菜大棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜?
24.(6分)已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
25.(7分)如图,在△ABC中,∠ACB为直角,AB上的高CD及中线CE恰好把∠ACB三等分,若AC=20,求△ABC的两锐角及AD、DE、EB各为多少?
26.(8分)已知:如图,等腰直角三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF,那么DE与DF具有怎样的关系?请说明理由.
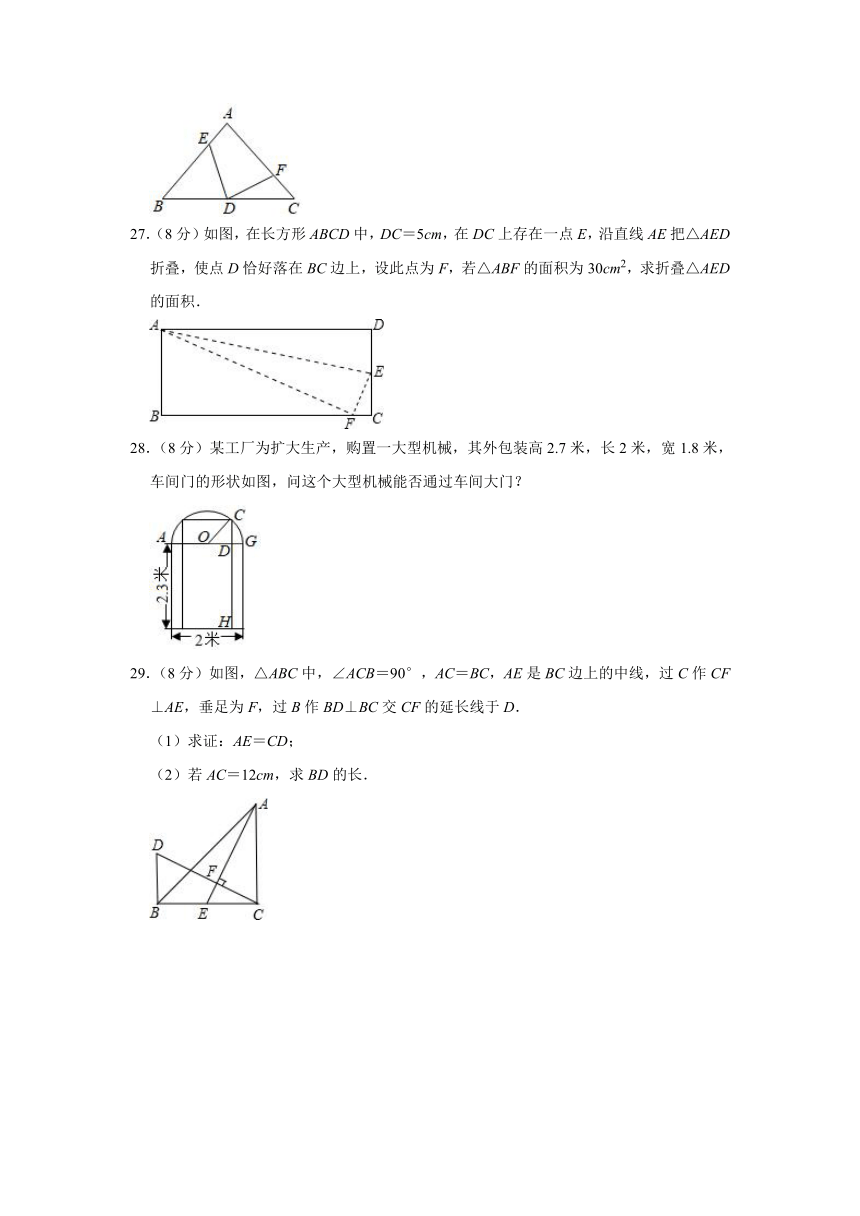
27.(8分)如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
28.(8分)某工厂为扩大生产,购置一大型机械,其外包装高2.7米,长2米,宽1.8米,车间门的形状如图,问这个大型机械能否通过车间大门?
29.(8分)如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
2020-2021学年山东省烟台市莱州市七年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题共10个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,请将正确答案的标号填在下表中)
1.下列图案中,有且只有三条对称轴的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形;
B、有四条对称轴;
C、不是轴对称图形;
D、有三条对称轴.
故选:D.
2.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
【分析】根据三角形的高解答即可.
【解答】解:△ABC的BC边上的高是AF,
故选:B.
3.下列各组数据能组成直角三角形的是( )
A.2,3,4 B.4,5,6 C.8,15,17 D.11,12,13
【分析】由82=64,152=225,172=289,64+225=289,可得出82+152=172,再利用勾股定理的逆定理,即可找出三边长分别为8,15,17的三角形为直角三角形.
【解答】解:∵82=64,152=225,172=289,64+225=289,
∴82+152=172,
∴三边长分别为8,15,17的三角形为直角三角形.
故选:C.
4.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是( )
A.30°、60° B.40°、70° C.50°、60° D.100°、30°
【分析】由三角形内角和定理和等腰三角形的判定分别对各个选项进行判断即可.
【解答】解:A、∵三角形中已知两个内角为30°、60°,
∴第三个内角为180°﹣30°﹣60°=90°,
∴这个三角形是直角三角形,不是等腰三角形,故选项A不符合题意;
B、∵三角形中已知两个内角为40°、70°,
∴第三个内角为180°﹣40°﹣70°=70°,
∴这个三角形由两个内角相等,
∴这个三角形是等腰三角形,故选项B符合题意;
C、∵三角形中已知两个内角为50°、60°,
∴第三个内角为180°﹣50°﹣60°=70°,
∴这个三角形不是等腰三角形,故选项C不符合题意;
D、∵三角形中已知两个内角为100°、30°,
∴第三个内角为180°﹣100°﹣30°=50°,
∴不是等腰三角形,故选项D不符合题意;
故选:B.
5.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
【分析】作出图形,延长AP与BC相交于点D,然后根据三角形的一个外角大于任何一个与它不相邻的内角解答.
【解答】解:如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选:A.
6.对于下列命题:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
【分析】根据轴对称的性质得到关于某一直线成轴对称的两个三角形全等,而两个全等三角形不一定是轴对称图形;等腰三角形的对称轴垂直平分底边,且平分顶角;一条线段的两个端点关于该线段的垂直平分线对称.
【解答】解:关于某一直线成轴对称的两个三角形全等,所以(1)为真命题;
等腰三角形的对称轴是直线而等腰三角形顶角的平分线为线段,所以(2)为假命题;
一条线段的两个端点关于该线段的垂直平分线对称,所以(3)为假命题;
两个全等三角形不一定是轴对称图形,所以(4)为假命题.
故选:B.
7.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.42或37
【分析】本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
【解答】解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD==9,
在Rt△ACD中,
CD==5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=9,
在Rt△ACD中,CD=5,
∴BC=9﹣5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故选:C.
8.如图,四边形ABCD是轴对称图形,直线AC是对称轴.如果∠BAD+∠BCD=170°,那么∠B等于( )
A.80° B.85° C.95° D.105°
【分析】根据四边形的内角和可求解∠B+∠D的度数,再由轴对称的性质可求解.
【解答】解:∵∠BAD+∠BCD=170°,∠BAD+∠BCD+∠B+∠D=360°,
∴∠B+∠D=190°,
由折叠可知:∠B=∠D,
∴∠B=95°.
故选:C.
9.如图,△ABC的三边AB、BC、CA长分别是10、15、20.其三条角平分线交于点O,将△ABC分为三个三角形,S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
【分析】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是10、15、20,所以面积之比就是2:4:4.
【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO=?AB?OE:?BC?OF:?AC?OD=AB:BC:AC=2:3:4,
故选:C.
10.如图,一架云梯25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
A.4米 B.6米 C.8米 D.10米
【分析】根据梯子长度不会变这个等量关系,我们可以根据BC求AC,根据AD、AC求CD,根据CD计算CE,根据CE,BC计算BE,即可解题.
【解答】解:由题意知AB=DE=25米,BC=7米,AD=4米,
∵在直角△ABC中,AC为直角边,
∴AC==24米,
已知AD=4米,则CD=24﹣4=20(米),
∵在直角△CDE中,CE为直角边
∴CE==15(米),
BE=15米﹣7米=8米.
故选:C.
二、填空题(本题共10个小题)
11.正五角星形共有 5 条对称轴.
【分析】根据轴对称图形的定义判断即可.
【解答】解:正五角星形共有5条对称轴.
故答案为:5.
12.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以 3 个三角形.
【分析】先以任意三条线段为一组分组,再根据三角形的任意两边之和大于第三边,任意两边之差小于第三边判断能否组成三角形.
【解答】解:任取三条线段为一组得:①1、2、3,②1、2、4,③1、2、5,④1、3、4,⑤1、3、5,⑥1、4、5,⑦2、3、4,⑧2、3、5,⑨2、4、5,⑩3、4、5,共十组,
①∵1+2=3,∴不能组成三角形;
②∵1+2=3<4,∴不能组成三角形;
③∵1+2=3<5,∴不能组成三角形;
④∵1+3=4,∴不能组成三角形;
⑤∵1+3=4<5,∴不能组成三角形;
⑥∵1+4=5,∴不能组成三角形;
⑦能够组成三角形;
⑧∵2+3=5,∴不能组成三角形;
⑨能够组成三角形;
⑩能够组成三角形.
故共可以组成3个形状不同的三角形.
13.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为 48 .
【分析】作出图形,过顶点A作AD⊥BC于D,根据等腰三角形三线合一的性质可得BD=BC,然后利用勾股定理列式求出AD,再根据三角形的面积公式列式计算即可得解.
【解答】解:如图,过顶点A作AD⊥BC于D,
则BD=BC=×12=6,
由勾股定理得,AD===8,
这个等腰三角形的面积=×12×8=48.
故答案为:48.
14.一帆船由于风向先向正西航行80千米,然后向正南航行150千米,这时它离出发点有 170 千米.
【分析】根据题意可知两次航向的方向构成了直角.然后根据题意知两次航行的路程即是两条直角边,根据勾股定理就能计算AC的长.
【解答】解:根据题意得:
AB=80,BC=150,
△ABC构成直角三角形,
根据勾股定理,
AC2=AB2+BC2,
∴AC2=802+1502,
∴AC=170千米.
答:这时它离出发点有170千米.
故答案为:170.
15.等腰三角形的两边长分别是6cm和4cm,那么第三边的长为 4cm或6cm .
【分析】题目给出等腰三角形有两条边长为6cm和4cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:由等腰三角形的概念,得
第三边的长可能为6cm和4cm,
即三角形的三边的长为4,4,6或4,6,6,
则第三边长为:4cm或6cm.
故答案为:4cm或6cm.
16.如图,在Rt△ABC中,B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C= 40° .
【分析】根据DE是AC的垂直平分线则AE=EC,根据等腰三角形等边对等角,以及直角三角形的两个锐角互余即可得到方程求得.
【解答】解:∵∠BAE:∠BAC=1:5,
∴设∠BAE=x°,则∠BAC=5x°,∠EAC=4x°,
∵DE是AC的垂直平分线,
∴AE=EC,
∴∠C=∠EAC=4x°,
∵在Rt△ABC中,∠BAC+∠C=90°,
∴5x+4x=90,
解得:x=10.
则∠C=40°.
故答案是:40°.
17.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 30 cm.
【分析】将长方形的盒子按不同方式展开,得到不同的矩形,求出不同矩形的对角线,最短者即为正确答案.
【解答】解:如图1所示,
AB==30(cm),
如图2所示:
AB==(cm).
∵30<,
∴蚂蚁爬行的最短路程是30cm.
故答案为:30.
18.如图,在△ABC中,DE是AC的垂直平分线,交BC于D,交AC于E,△ABD的周长为15cm,而AC=5cm,则△ABC的周长是 20cm .
【分析】根据线段垂直平分线的性质得到DA=DC,则利用等线段代换得到AB+BC=15,然后计算△ABC的周长.
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∵△ABD的周长为15cm,
∴AB+BD+DA=15,
∴AB+BD+DC=15,
即AB+BC=15,
∴△ABC的周长=AB+BC+AC=15+5=20(cm).
故答案为20cm.
19.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,月S△ABC=32cm2,则S阴影等于 8cm2 .
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.
【解答】解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×32=16(cm2),
∴S△BCE=S△ABC=×32=16(cm2),
∵点F是CE的中点,
∴S△BEF=S△BCE=×16=8(cm2).
故答案为:8cm2.
20.如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD= 5cm .
【分析】过M作MF⊥AC于F,先根据角平分线的性质得出MD=MF,再由角平分线的定义及平行线的性质得出∠CAM=∠AME=15°,由三角形外角的性质得出∠CEM=30°,从而在Rt△MEF中,利用30°角所对的直角边等于斜边的一半,得出MF=ME.
【解答】解:过M作MF⊥AC于F,
∵AM是∠BAC的角平分线,
∴MD=MF,∠BAM=∠CAM,
∵ME∥BA,
∴∠AME=∠BAM,
∴∠CAM=∠AME=∠BAC=×30°=15°,
∵∠CEM是△AME的外角,
∴∠CEM=∠CAM+∠AME=15°+15°=30°,
在Rt△MEF中,∠FEM=30°,
∴MF=ME=×10=5cm,
∴MD=MF=5cm.
故答案为5cm.
三、解答题(本题共9个小题)
21.(5分)如图,图中的图形是轴对称图形吗?如果是轴对称图形,请作出它们的对称轴.
【分析】根据轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴可得到答案.
【解答】解:第1,2,3,5个图形是轴对称图形;第4个图形不是轴对称图形.
如图所示:
22.(5分)如图,已知线段a、c和m,求作:△ABC,使BC=a,AB=c,BC边上的中线AM=m.
要求:不写作法,保留作图痕迹,标注字母.
【分析】首先要确定出底边,先作出线段BC=a,然后找出BC的中点,分别以B、BC中点为圆心,以c、m为半径作弧,两弧的交点即为A点,由此确定出所求作的三角形.
【解答】解:如图;
作法:1、作线段BC=a;
2、取线段的BC的中点,分别以B、BC中点为圆心,以c、m为半径作弧,两弧交于点A;
3、连接AB、AC;
结论:△ABC是所求作的三角形.
23.(5分)如图,一菜农要修建蔬菜大棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜?
【分析】在侧面的直角三角形中,由勾股定理可得直角三角形的斜边长.棚顶是以侧面的斜边为宽,棚的长为长的矩形,依据矩形的面积公式即可求解.
【解答】解:由题意可知,△AEB是直角三角形,其中AE=1.5m,BE=2m,
由勾股定理可得AE2+BE2=AB2,
即1.52+22=AB2,
所以AB=2.5m,
18×2.5=45(m2).
所以共需这种塑料薄膜45m2.
24.(6分)已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
【分析】先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
【解答】解:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBA﹣∠OCA=60°,
所以,∠BOC=180°﹣60°=120°.
25.(7分)如图,在△ABC中,∠ACB为直角,AB上的高CD及中线CE恰好把∠ACB三等分,若AC=20,求△ABC的两锐角及AD、DE、EB各为多少?
【分析】首先利用条件可得推出∠ACD=∠DCE=∠ECB=30°,再利用直角三角形30°角所对的直角边是斜边的一半可得答案.
【解答】解:∵△ABC中,∠C为直角,AB上的高CD及中线CE恰好把∠ACB三等分,
∴∠ACD=∠DCE=∠ECB=30°,
又∵CD⊥AB,AC=20,
∴∠A=60°,AD=10,
∵∠ACB为直角,
∴∠B=30°
∵AC=20,
∴AB=40,
∵CE是△ABC中线,
∴AE=BE=20,
∴DE=10.
26.(8分)已知:如图,等腰直角三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF,那么DE与DF具有怎样的关系?请说明理由.
【分析】根据等腰直角三角形的性质得到∠C=45°,中线AD平分∠BAC,并且AD=BC,则∠BAD=∠C,AD=DC,又EA=CF,根据全等三角形的判定易得到△ADE≌△CDF,然后根据全等三角形的性质即可得到结论.
【解答】解:DE与DF相等并且互相垂直,连接AD,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,
∵D为BC中点,
∴AD=BD=CD,AD⊥BC,
∴∠B=∠DAB=∠DAC=∠C=45°,
在△AED和△CFD中,
,
∴△AED≌△CFD(SAS);
∴DE=DF,∠ADE=∠CDF,
∵AD⊥BC,
∴∠ADC=90°,
即∠ADF+∠FDC=90°,
∴∠ADF+∠ADE=90°,
∴DE⊥DF.
27.(8分)如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
【分析】根据三角形的面积求得BF的长,再根据勾股定理求得AF的长,即为AD的长;设DE=x,则EC=5﹣x,EF=x.根据勾股定理列方程求得x的值,进而求得△AED的面积.
【解答】解:由折叠的对称性,得AD=AF,DE=EF.
由S△ABF=BF?AB=30,AB=5,
得BF=12.
在Rt△ABF中,由勾股定理,得
.
所以AD=13.
设DE=x,则EC=5﹣x,EF=x,FC=1,
在Rt△ECF中,EC2+FC2=EF2,
即(5﹣x)2+12=x2.
解得.
故.
28.(8分)某工厂为扩大生产,购置一大型机械,其外包装高2.7米,长2米,宽1.8米,车间门的形状如图,问这个大型机械能否通过车间大门?
【分析】根据勾股定理得出CD的长,进而得出CH的长,即可判定.
【解答】解:点D在车门中线0.9米处,且CD⊥AG,与地面交于H,
OC=OG=AG=1米,OD=0.9米,
在Rt△OCD中,由勾股定理得:
CD2=OC2﹣OD2=12﹣0.92=0.19,
∴CH=CD+DH=+2.3≈2.8>2.7,
∴这个大型机械能通过车间大门.
29.(8分)如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
【分析】(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得BD=EC=BC=AC,且AC=12,即可求出BD的长.
【解答】(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:∵△CDB≌△AEC,
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=BC=AC,且AC=12cm.
∴BD=6cm.
一、选择题(本题共10个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,请将正确答案的标号填在下表中)
1.下列图案中,有且只有三条对称轴的是( )
A. B. C. D.
2.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
3.下列各组数据能组成直角三角形的是( )
A.2,3,4 B.4,5,6 C.8,15,17 D.11,12,13
4.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是( )
A.30°、60° B.40°、70° C.50°、60° D.100°、30°
5.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
6.对于下列命题:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
7.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.42或37
8.如图,四边形ABCD是轴对称图形,直线AC是对称轴.如果∠BAD+∠BCD=170°,那么∠B等于( )
A.80° B.85° C.95° D.105°
9.如图,△ABC的三边AB、BC、CA长分别是10、15、20.其三条角平分线交于点O,将△ABC分为三个三角形,S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
10.如图,一架云梯25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
A.4米 B.6米 C.8米 D.10米
二、填空题(本题共10个小题)
11.正五角星形共有 条对称轴.
12.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以 个三角形.
13.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为 .
14.一帆船由于风向先向正西航行80千米,然后向正南航行150千米,这时它离出发点有 千米.
15.等腰三角形的两边长分别是6cm和4cm,那么第三边的长为 .
16.如图,在Rt△ABC中,B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C= .
17.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 cm.
18.如图,在△ABC中,DE是AC的垂直平分线,交BC于D,交AC于E,△ABD的周长为15cm,而AC=5cm,则△ABC的周长是 .
19.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,月S△ABC=32cm2,则S阴影等于 .
20.如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD= .
三、解答题(本题共9个小题)
21.(5分)如图,图中的图形是轴对称图形吗?如果是轴对称图形,请作出它们的对称轴.
22.(5分)如图,已知线段a、c和m,求作:△ABC,使BC=a,AB=c,BC边上的中线AM=m.
要求:不写作法,保留作图痕迹,标注字母.
23.(5分)如图,一菜农要修建蔬菜大棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜?
24.(6分)已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
25.(7分)如图,在△ABC中,∠ACB为直角,AB上的高CD及中线CE恰好把∠ACB三等分,若AC=20,求△ABC的两锐角及AD、DE、EB各为多少?
26.(8分)已知:如图,等腰直角三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF,那么DE与DF具有怎样的关系?请说明理由.
27.(8分)如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
28.(8分)某工厂为扩大生产,购置一大型机械,其外包装高2.7米,长2米,宽1.8米,车间门的形状如图,问这个大型机械能否通过车间大门?
29.(8分)如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
2020-2021学年山东省烟台市莱州市七年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题共10个小题,每小题均给出标号为A,B,C,D的四个备选答案,其中只有一个是正确的,请将正确答案的标号填在下表中)
1.下列图案中,有且只有三条对称轴的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形;
B、有四条对称轴;
C、不是轴对称图形;
D、有三条对称轴.
故选:D.
2.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
【分析】根据三角形的高解答即可.
【解答】解:△ABC的BC边上的高是AF,
故选:B.
3.下列各组数据能组成直角三角形的是( )
A.2,3,4 B.4,5,6 C.8,15,17 D.11,12,13
【分析】由82=64,152=225,172=289,64+225=289,可得出82+152=172,再利用勾股定理的逆定理,即可找出三边长分别为8,15,17的三角形为直角三角形.
【解答】解:∵82=64,152=225,172=289,64+225=289,
∴82+152=172,
∴三边长分别为8,15,17的三角形为直角三角形.
故选:C.
4.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是( )
A.30°、60° B.40°、70° C.50°、60° D.100°、30°
【分析】由三角形内角和定理和等腰三角形的判定分别对各个选项进行判断即可.
【解答】解:A、∵三角形中已知两个内角为30°、60°,
∴第三个内角为180°﹣30°﹣60°=90°,
∴这个三角形是直角三角形,不是等腰三角形,故选项A不符合题意;
B、∵三角形中已知两个内角为40°、70°,
∴第三个内角为180°﹣40°﹣70°=70°,
∴这个三角形由两个内角相等,
∴这个三角形是等腰三角形,故选项B符合题意;
C、∵三角形中已知两个内角为50°、60°,
∴第三个内角为180°﹣50°﹣60°=70°,
∴这个三角形不是等腰三角形,故选项C不符合题意;
D、∵三角形中已知两个内角为100°、30°,
∴第三个内角为180°﹣100°﹣30°=50°,
∴不是等腰三角形,故选项D不符合题意;
故选:B.
5.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( )
A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
【分析】作出图形,延长AP与BC相交于点D,然后根据三角形的一个外角大于任何一个与它不相邻的内角解答.
【解答】解:如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选:A.
6.对于下列命题:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
【分析】根据轴对称的性质得到关于某一直线成轴对称的两个三角形全等,而两个全等三角形不一定是轴对称图形;等腰三角形的对称轴垂直平分底边,且平分顶角;一条线段的两个端点关于该线段的垂直平分线对称.
【解答】解:关于某一直线成轴对称的两个三角形全等,所以(1)为真命题;
等腰三角形的对称轴是直线而等腰三角形顶角的平分线为线段,所以(2)为假命题;
一条线段的两个端点关于该线段的垂直平分线对称,所以(3)为假命题;
两个全等三角形不一定是轴对称图形,所以(4)为假命题.
故选:B.
7.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.42或37
【分析】本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
【解答】解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD==9,
在Rt△ACD中,
CD==5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=9,
在Rt△ACD中,CD=5,
∴BC=9﹣5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故选:C.
8.如图,四边形ABCD是轴对称图形,直线AC是对称轴.如果∠BAD+∠BCD=170°,那么∠B等于( )
A.80° B.85° C.95° D.105°
【分析】根据四边形的内角和可求解∠B+∠D的度数,再由轴对称的性质可求解.
【解答】解:∵∠BAD+∠BCD=170°,∠BAD+∠BCD+∠B+∠D=360°,
∴∠B+∠D=190°,
由折叠可知:∠B=∠D,
∴∠B=95°.
故选:C.
9.如图,△ABC的三边AB、BC、CA长分别是10、15、20.其三条角平分线交于点O,将△ABC分为三个三角形,S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
【分析】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是10、15、20,所以面积之比就是2:4:4.
【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO=?AB?OE:?BC?OF:?AC?OD=AB:BC:AC=2:3:4,
故选:C.
10.如图,一架云梯25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
A.4米 B.6米 C.8米 D.10米
【分析】根据梯子长度不会变这个等量关系,我们可以根据BC求AC,根据AD、AC求CD,根据CD计算CE,根据CE,BC计算BE,即可解题.
【解答】解:由题意知AB=DE=25米,BC=7米,AD=4米,
∵在直角△ABC中,AC为直角边,
∴AC==24米,
已知AD=4米,则CD=24﹣4=20(米),
∵在直角△CDE中,CE为直角边
∴CE==15(米),
BE=15米﹣7米=8米.
故选:C.
二、填空题(本题共10个小题)
11.正五角星形共有 5 条对称轴.
【分析】根据轴对称图形的定义判断即可.
【解答】解:正五角星形共有5条对称轴.
故答案为:5.
12.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以 3 个三角形.
【分析】先以任意三条线段为一组分组,再根据三角形的任意两边之和大于第三边,任意两边之差小于第三边判断能否组成三角形.
【解答】解:任取三条线段为一组得:①1、2、3,②1、2、4,③1、2、5,④1、3、4,⑤1、3、5,⑥1、4、5,⑦2、3、4,⑧2、3、5,⑨2、4、5,⑩3、4、5,共十组,
①∵1+2=3,∴不能组成三角形;
②∵1+2=3<4,∴不能组成三角形;
③∵1+2=3<5,∴不能组成三角形;
④∵1+3=4,∴不能组成三角形;
⑤∵1+3=4<5,∴不能组成三角形;
⑥∵1+4=5,∴不能组成三角形;
⑦能够组成三角形;
⑧∵2+3=5,∴不能组成三角形;
⑨能够组成三角形;
⑩能够组成三角形.
故共可以组成3个形状不同的三角形.
13.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为 48 .
【分析】作出图形,过顶点A作AD⊥BC于D,根据等腰三角形三线合一的性质可得BD=BC,然后利用勾股定理列式求出AD,再根据三角形的面积公式列式计算即可得解.
【解答】解:如图,过顶点A作AD⊥BC于D,
则BD=BC=×12=6,
由勾股定理得,AD===8,
这个等腰三角形的面积=×12×8=48.
故答案为:48.
14.一帆船由于风向先向正西航行80千米,然后向正南航行150千米,这时它离出发点有 170 千米.
【分析】根据题意可知两次航向的方向构成了直角.然后根据题意知两次航行的路程即是两条直角边,根据勾股定理就能计算AC的长.
【解答】解:根据题意得:
AB=80,BC=150,
△ABC构成直角三角形,
根据勾股定理,
AC2=AB2+BC2,
∴AC2=802+1502,
∴AC=170千米.
答:这时它离出发点有170千米.
故答案为:170.
15.等腰三角形的两边长分别是6cm和4cm,那么第三边的长为 4cm或6cm .
【分析】题目给出等腰三角形有两条边长为6cm和4cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:由等腰三角形的概念,得
第三边的长可能为6cm和4cm,
即三角形的三边的长为4,4,6或4,6,6,
则第三边长为:4cm或6cm.
故答案为:4cm或6cm.
16.如图,在Rt△ABC中,B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C= 40° .
【分析】根据DE是AC的垂直平分线则AE=EC,根据等腰三角形等边对等角,以及直角三角形的两个锐角互余即可得到方程求得.
【解答】解:∵∠BAE:∠BAC=1:5,
∴设∠BAE=x°,则∠BAC=5x°,∠EAC=4x°,
∵DE是AC的垂直平分线,
∴AE=EC,
∴∠C=∠EAC=4x°,
∵在Rt△ABC中,∠BAC+∠C=90°,
∴5x+4x=90,
解得:x=10.
则∠C=40°.
故答案是:40°.
17.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 30 cm.
【分析】将长方形的盒子按不同方式展开,得到不同的矩形,求出不同矩形的对角线,最短者即为正确答案.
【解答】解:如图1所示,
AB==30(cm),
如图2所示:
AB==(cm).
∵30<,
∴蚂蚁爬行的最短路程是30cm.
故答案为:30.
18.如图,在△ABC中,DE是AC的垂直平分线,交BC于D,交AC于E,△ABD的周长为15cm,而AC=5cm,则△ABC的周长是 20cm .
【分析】根据线段垂直平分线的性质得到DA=DC,则利用等线段代换得到AB+BC=15,然后计算△ABC的周长.
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∵△ABD的周长为15cm,
∴AB+BD+DA=15,
∴AB+BD+DC=15,
即AB+BC=15,
∴△ABC的周长=AB+BC+AC=15+5=20(cm).
故答案为20cm.
19.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,月S△ABC=32cm2,则S阴影等于 8cm2 .
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.
【解答】解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×32=16(cm2),
∴S△BCE=S△ABC=×32=16(cm2),
∵点F是CE的中点,
∴S△BEF=S△BCE=×16=8(cm2).
故答案为:8cm2.
20.如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD= 5cm .
【分析】过M作MF⊥AC于F,先根据角平分线的性质得出MD=MF,再由角平分线的定义及平行线的性质得出∠CAM=∠AME=15°,由三角形外角的性质得出∠CEM=30°,从而在Rt△MEF中,利用30°角所对的直角边等于斜边的一半,得出MF=ME.
【解答】解:过M作MF⊥AC于F,
∵AM是∠BAC的角平分线,
∴MD=MF,∠BAM=∠CAM,
∵ME∥BA,
∴∠AME=∠BAM,
∴∠CAM=∠AME=∠BAC=×30°=15°,
∵∠CEM是△AME的外角,
∴∠CEM=∠CAM+∠AME=15°+15°=30°,
在Rt△MEF中,∠FEM=30°,
∴MF=ME=×10=5cm,
∴MD=MF=5cm.
故答案为5cm.
三、解答题(本题共9个小题)
21.(5分)如图,图中的图形是轴对称图形吗?如果是轴对称图形,请作出它们的对称轴.
【分析】根据轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴可得到答案.
【解答】解:第1,2,3,5个图形是轴对称图形;第4个图形不是轴对称图形.
如图所示:
22.(5分)如图,已知线段a、c和m,求作:△ABC,使BC=a,AB=c,BC边上的中线AM=m.
要求:不写作法,保留作图痕迹,标注字母.
【分析】首先要确定出底边,先作出线段BC=a,然后找出BC的中点,分别以B、BC中点为圆心,以c、m为半径作弧,两弧的交点即为A点,由此确定出所求作的三角形.
【解答】解:如图;
作法:1、作线段BC=a;
2、取线段的BC的中点,分别以B、BC中点为圆心,以c、m为半径作弧,两弧交于点A;
3、连接AB、AC;
结论:△ABC是所求作的三角形.
23.(5分)如图,一菜农要修建蔬菜大棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜?
【分析】在侧面的直角三角形中,由勾股定理可得直角三角形的斜边长.棚顶是以侧面的斜边为宽,棚的长为长的矩形,依据矩形的面积公式即可求解.
【解答】解:由题意可知,△AEB是直角三角形,其中AE=1.5m,BE=2m,
由勾股定理可得AE2+BE2=AB2,
即1.52+22=AB2,
所以AB=2.5m,
18×2.5=45(m2).
所以共需这种塑料薄膜45m2.
24.(6分)已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
【分析】先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
【解答】解:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBA﹣∠OCA=60°,
所以,∠BOC=180°﹣60°=120°.
25.(7分)如图,在△ABC中,∠ACB为直角,AB上的高CD及中线CE恰好把∠ACB三等分,若AC=20,求△ABC的两锐角及AD、DE、EB各为多少?
【分析】首先利用条件可得推出∠ACD=∠DCE=∠ECB=30°,再利用直角三角形30°角所对的直角边是斜边的一半可得答案.
【解答】解:∵△ABC中,∠C为直角,AB上的高CD及中线CE恰好把∠ACB三等分,
∴∠ACD=∠DCE=∠ECB=30°,
又∵CD⊥AB,AC=20,
∴∠A=60°,AD=10,
∵∠ACB为直角,
∴∠B=30°
∵AC=20,
∴AB=40,
∵CE是△ABC中线,
∴AE=BE=20,
∴DE=10.
26.(8分)已知:如图,等腰直角三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF,那么DE与DF具有怎样的关系?请说明理由.
【分析】根据等腰直角三角形的性质得到∠C=45°,中线AD平分∠BAC,并且AD=BC,则∠BAD=∠C,AD=DC,又EA=CF,根据全等三角形的判定易得到△ADE≌△CDF,然后根据全等三角形的性质即可得到结论.
【解答】解:DE与DF相等并且互相垂直,连接AD,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,
∵D为BC中点,
∴AD=BD=CD,AD⊥BC,
∴∠B=∠DAB=∠DAC=∠C=45°,
在△AED和△CFD中,
,
∴△AED≌△CFD(SAS);
∴DE=DF,∠ADE=∠CDF,
∵AD⊥BC,
∴∠ADC=90°,
即∠ADF+∠FDC=90°,
∴∠ADF+∠ADE=90°,
∴DE⊥DF.
27.(8分)如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
【分析】根据三角形的面积求得BF的长,再根据勾股定理求得AF的长,即为AD的长;设DE=x,则EC=5﹣x,EF=x.根据勾股定理列方程求得x的值,进而求得△AED的面积.
【解答】解:由折叠的对称性,得AD=AF,DE=EF.
由S△ABF=BF?AB=30,AB=5,
得BF=12.
在Rt△ABF中,由勾股定理,得
.
所以AD=13.
设DE=x,则EC=5﹣x,EF=x,FC=1,
在Rt△ECF中,EC2+FC2=EF2,
即(5﹣x)2+12=x2.
解得.
故.
28.(8分)某工厂为扩大生产,购置一大型机械,其外包装高2.7米,长2米,宽1.8米,车间门的形状如图,问这个大型机械能否通过车间大门?
【分析】根据勾股定理得出CD的长,进而得出CH的长,即可判定.
【解答】解:点D在车门中线0.9米处,且CD⊥AG,与地面交于H,
OC=OG=AG=1米,OD=0.9米,
在Rt△OCD中,由勾股定理得:
CD2=OC2﹣OD2=12﹣0.92=0.19,
∴CH=CD+DH=+2.3≈2.8>2.7,
∴这个大型机械能通过车间大门.
29.(8分)如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
【分析】(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得BD=EC=BC=AC,且AC=12,即可求出BD的长.
【解答】(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:∵△CDB≌△AEC,
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=BC=AC,且AC=12cm.
∴BD=6cm.
同课章节目录
