2020-2021学年人教版七年级数学下册开学考试复习试卷1(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册开学考试复习试卷1(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 13:54:10 | ||
图片预览




文档简介
2020-2021学年人教版七年级数学下册开学考试复习试卷1
一.选择题(共12小题,满分36分,每小题3分)
1.下列方程是二元一次方程的是( )
A.﹣y+xy=2
B.3x﹣11=5x
C.3x=2+y
D.﹣=
2.一个正数a的平方根是2x﹣3与5﹣x,则这个正数a的值是( )
A.25
B.49
C.64
D.81
3.下列各组数的大小关系正确的是( )
A.+0.3<﹣0.1
B.0<﹣|﹣7|
C.﹣<﹣1.414
D.﹣>﹣
4.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3)
B.(﹣5,3)
C.(3,﹣5)
D.(﹣3,5)
5.如图,∠CED=60°,DF⊥AB于点F,DM∥AC交AB于点M,DE∥AB交AC于点E,则∠MDF的度数是( )
A.60°
B.40°
C.30°
D.20°
6.下列说法中正确的是( )
A.在同一平面内,不重合的两条直线的位置关系为平行或垂直
B.直线外一点到这条直线的垂线段叫这点到这条直线的距离
C.同旁内角互补
D.两点之间线段最短
7.点P(t+3,t+2)在直角坐标系的x轴上,则P点坐标为( )
A.(0,﹣2)
B.(﹣2,0)
C.(1,2)
D.(1,0)
8.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80°
B.85°
C.90°
D.95°
9.已知点P(3a,a+2)在x轴上,则P点的坐标是( )
A.(3,2)
B.(6,0)
C.(﹣6,0)
D.(6,2)
10.某市举办中学生足球赛,按比赛规则,每场比赛都要分出胜负,胜1场得3分,负一场扣1分,菁英中学队在8场比赛中得到12分,若设该队胜的场数为x,负的场数为y,则可列方程组为( )
A.
B.
C.
D.
11.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1
B.2
C.3
D.4
12.若两条直线被第三条直线所截,有一对同位角相等,则其中一对同旁内角的角平分线( )
A.互相垂直
B.互相平行
C.相交或平行
D.不相等
二.填空题(共6小题,满分18分,每小题3分)
13.下列关于有理数和无理数的说法:①有限小数和无限循环小数都是有理数;②无限不循环小数是无理数;③无理数都是无限小数;④任何有理数都能表示成两个整数之比.其中说法正确的是
.(填序号)
14.已知x是的整数部分,y是的小数部分,则xy的值
.
15.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为
.
16.如图,将一副三角板按如图放置,则下列结论:
①∠1=∠3;
②如果∠2=30°,则有BC∥AE;
③如果∠1=∠2=∠3,则有BC∥AE;
④如果∠2=45°,必有∠4=∠E.其中正确的有
(填序号).
17.三个同学对问题“若方程组,的解是,求方程组的解.”提出各自的想法:甲说:“这个题目好象条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“可以把第二个方程组的两个方程的两边都除以7,通过换元替换的方法来解决.”参考他们的讨论,你认为这题目的解应该是:
.
18.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
°.
三.解答题(共8小题,满分66分)
19.(6分)计算:
(1)﹣|2﹣|﹣+2;
(2)3﹣|﹣|.
20.(6分)解方组:
(1);
(2).
21.(8分)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
22.(8分)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
23.(9分)某环卫公司通过政府采购的方式计划购进一批A,B两种型号的新能源汽车.据了解,2辆A型汽车和3辆B型汽车的进价共计80万元;3辆A型汽车和2辆B型汽车的进价共计95万元.
(1)求A,B两种型号的汽车每辆进价分别为多少万元;
(2)该公司计划恰好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),并使得购进的B种型号的新能源汽车数量多于A种型号的新能源汽车数量,请直接写出该公司的采购方案.
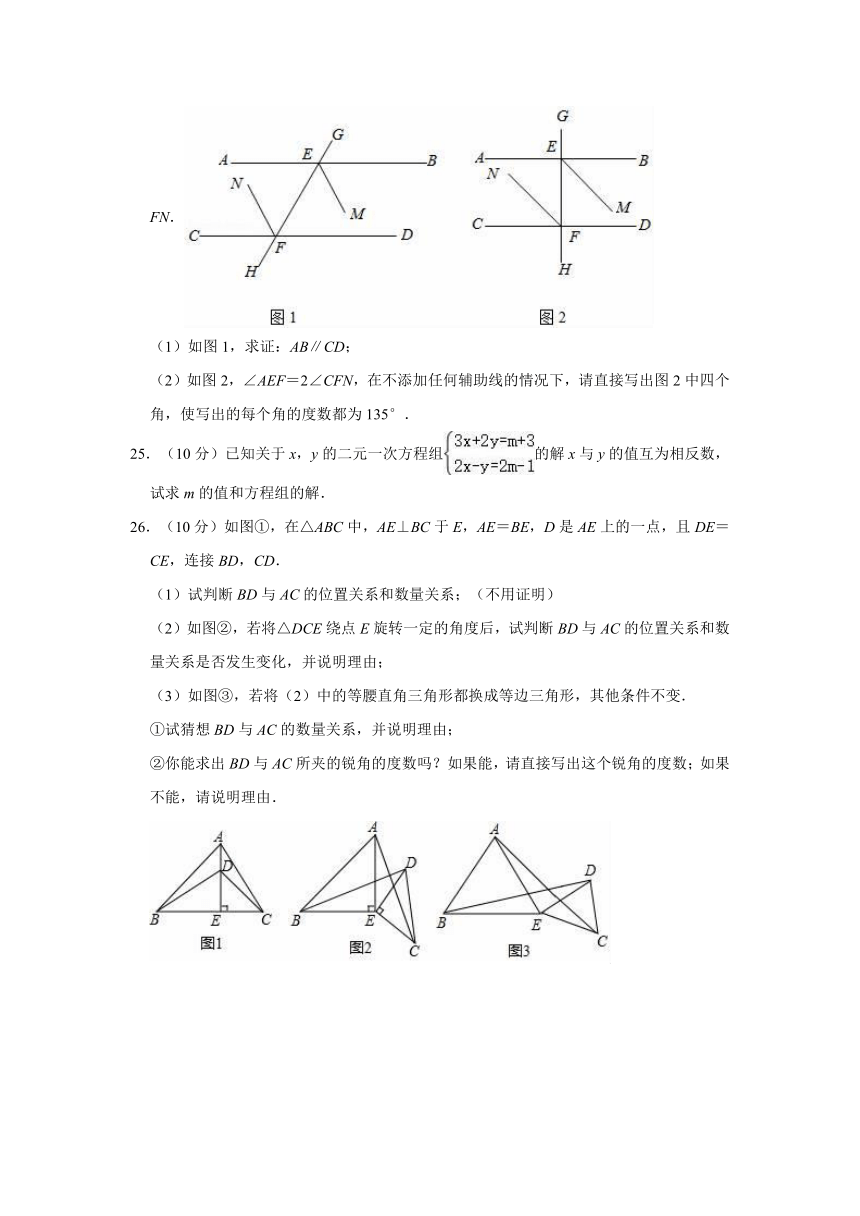
24.(9分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
25.(10分)已知关于x,y的二元一次方程组的解x与y的值互为相反数,试求m的值和方程组的解.
26.(10分)如图①,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系;(不用证明)
(2)如图②,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图③,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC所夹的锐角的度数吗?如果能,请直接写出这个锐角的度数;如果不能,请说明理由.
2021年02月15日宫老师的初中数学平行组卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、﹣y+xy=2,是二元二次方程,不合题意;
B、3x﹣11=5x,是一元一次方程,不合题意;
C、3x=2+y,是二元一次方程,符合题意;
D、﹣=,是分式方程,不合题意;
故选:C.
2.解:由正数的两个平方根互为相反数可得
(2x﹣3)+(5﹣x)=0,
解得x=﹣2,
所以5﹣x=5﹣(﹣2)=7,
所以a=72=49.
故选:B.
3.解:A、+0.3>﹣0.1,故本选项不符合题意;
B、0>﹣|﹣7|,故本选项不符合题意;
C、∵1.4142=1.999396,
∴﹣<﹣1.414,故本选项符合题意;
D、﹣<﹣,故本选项不符合题意;
故选:C.
4.解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
故选:D.
5.解:∵DE∥AB
∴∠A=∠CED=60°,
∵DM∥AC
∴∠DMF=∠A=60°,
∵DF⊥AB
∠DFM=90°,
∴∠MDF=90°﹣60°=30°.
故选:C.
6.解:A、在同一平面内,两条直线的位置只有两种:相交和平行,垂直是相交的一种情况,故A错误;
B、点到直线的距离指的是线段的长度,而非垂线段,故B错误;
C、两直线平行,同旁内角互补,故C错误;
D、两点之间线段最短,故D正确.
故选:D.
7.解:∵点P(t+3,t+2)在直角坐标系的x轴上,
∴t+2=0,
解得:t=﹣2,
故t+3=1,
则P点坐标为(1,0).
故选:D.
8.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
9.解:∵点P(3a,a+2)在x轴上,
∴y=0,
即a+2=0,
解得a=﹣2,
∴3a=﹣6,
∴点P的坐标为(﹣6,0).
故选:C.
10.解:依题意得:.
故选:C.
11.解:①将a=1代入原方程组,得解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
若x,y是互为相反数,则x+y=0,
即2a+1+2﹣2a=0,方程无解.
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
12.解:如图,
∵∠APE=∠CQE,
∴AB∥CD,
∴∠BPQ+∠DQP=180°,
∵PM平分∠BPQ,QN平分∠DQP,
∴∠BPQ=2∠MPQ,∠DQP=2∠NQP,
∴∠MPQ+∠NQP=90°,
∴∠POQ=90°,
即PM⊥QN,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
13.解:①任何有限小数或无限循环小数都是有理数,正确;
②无限不循环小数是无理数,正确;
③无理数都是无限小数,正确;
④有理数包括整数和分数,整数可以表示为整数:1的形式,分数本身就是分子:分母的形式,正确.
故答案为:①②③④.
14.解:∵x是的整数部分,
∴x=2,
∵y是的小数部分,
∴y=﹣2,
∴yx=2(﹣2)=2﹣4,
故答案为2﹣4.
15.解:将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
16.解:∵∠EAD=∠CAB=90°,
∴∠1=∠3,故①正确,
当∠2=30°时,∠3=60°,∠4=45°,
∴∠3≠∠4,
故AE与BC不平行,故②错误,
当∠1=∠2=∠3时,可得∠3=∠4=45°,
∴BC∥AE,故③正确,
∵∠E=60°,∠4=45°,
∴∠E≠∠4,故④错误,
故答案为:①③.
17.解:,
两边同时除以7得,
,
∵方程组的解是,
∴,
解得:;
故答案为:.
18.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=92°,
∴∠CFE=92°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣92°=23°.
故答案为:23.
三.解答题(共8小题,满分66分)
19.解:(1)﹣|2﹣|﹣+2
=﹣4﹣+2﹣3+2
=﹣5.
(2)3﹣|﹣|
=3﹣+
=4﹣.
20.解:,
②×3﹣①×2,得11x=﹣15,解得x=﹣,
把x=﹣代入①,得,解得y=,
故原方程组的解为;
(2)原方程组可化为,
①﹣②,得4y=8,解得y=2,
把y=2代入②,得2x﹣2=4,解得x=3,
故方程组的解为.
21.解:(1)C(0,2),D(4,2)
S四边形ABDC=AB?OC=4×2=8;
(2)存在,当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
22.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
23.解:(1)设A型汽车每辆的进价为x万元,B型汽车每辆的进价为y万元,
依题意,得:,
解得:,
答:A型汽车每辆的进价为25万元,B型汽车每辆的进价为10万元.
(2)设购进A型汽车m辆,购进B型汽车n辆,m<n,
依题意,得:25m+10n=200,
∴m=8﹣n.
∵m,n均为正整数,
∴n为5的倍数,
∴或或,
∵m<n,
∴不合题意舍去,
∴共2种购买方案,
方案一:购进A型车4辆,B型车10辆;
方案二:购进A型车2辆,B型车15辆.
24.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
25.解:方程组,
②×2+①得7x=5m+1,
∴x=,
将x=代入②,得y=,
∵x与y的值互为相反数,
∴+=0
∴m=﹣10,
∴x=﹣7,y=7,
∴原方程组的解为.
26.解:(1)结论:BD=AC,BD⊥AC.
理由:延长BD交AC于F.
∵AE⊥CB
∴∠AEC=∠BED=90°.
在△AEC和△BED中,
,
∴△AEC≌△BED,
∴AC=BD,∠CAE=∠EBD,
∵∠AEC=90°,
∴∠C+∠CAE=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴AC⊥BD.
(2)如图2中,不发生变化,设DE与AC交于点O,BD与AC交于点F.
理由是:∵∠BEA=∠DEC=90°,∴∠BEA+∠AED=∠DEC+∠AED,∴∠BED=∠AEC,
在△BED和△AEC中,
,
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,
∵∠DEC=90°,
∴∠ACE+∠EOC=90°,
∵∠EOC=∠DOF,
∴∠BDE+∠DOF=90°,
∴∠DFO=180°﹣90°=90°,
∴BD⊥AC;
(3)①如图3中,结论:BD=AC,
理由是:∵△ABE和△DEC是等边三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
,
∴△BED≌△AEC,
∴BD=AC.
②能;设BD与AC交于点F,由△BED≌△AEC可知,∠BDE=∠ACE,
∴∠DFC=180°﹣(∠BDE+∠EDC+∠DCF)=180°﹣(∠ACE+∠EDC+∠DCF)=180°﹣(60°+60°)=60°,
即BD与AC所成的锐角的度数为60°.
一.选择题(共12小题,满分36分,每小题3分)
1.下列方程是二元一次方程的是( )
A.﹣y+xy=2
B.3x﹣11=5x
C.3x=2+y
D.﹣=
2.一个正数a的平方根是2x﹣3与5﹣x,则这个正数a的值是( )
A.25
B.49
C.64
D.81
3.下列各组数的大小关系正确的是( )
A.+0.3<﹣0.1
B.0<﹣|﹣7|
C.﹣<﹣1.414
D.﹣>﹣
4.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3)
B.(﹣5,3)
C.(3,﹣5)
D.(﹣3,5)
5.如图,∠CED=60°,DF⊥AB于点F,DM∥AC交AB于点M,DE∥AB交AC于点E,则∠MDF的度数是( )
A.60°
B.40°
C.30°
D.20°
6.下列说法中正确的是( )
A.在同一平面内,不重合的两条直线的位置关系为平行或垂直
B.直线外一点到这条直线的垂线段叫这点到这条直线的距离
C.同旁内角互补
D.两点之间线段最短
7.点P(t+3,t+2)在直角坐标系的x轴上,则P点坐标为( )
A.(0,﹣2)
B.(﹣2,0)
C.(1,2)
D.(1,0)
8.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80°
B.85°
C.90°
D.95°
9.已知点P(3a,a+2)在x轴上,则P点的坐标是( )
A.(3,2)
B.(6,0)
C.(﹣6,0)
D.(6,2)
10.某市举办中学生足球赛,按比赛规则,每场比赛都要分出胜负,胜1场得3分,负一场扣1分,菁英中学队在8场比赛中得到12分,若设该队胜的场数为x,负的场数为y,则可列方程组为( )
A.
B.
C.
D.
11.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1
B.2
C.3
D.4
12.若两条直线被第三条直线所截,有一对同位角相等,则其中一对同旁内角的角平分线( )
A.互相垂直
B.互相平行
C.相交或平行
D.不相等
二.填空题(共6小题,满分18分,每小题3分)
13.下列关于有理数和无理数的说法:①有限小数和无限循环小数都是有理数;②无限不循环小数是无理数;③无理数都是无限小数;④任何有理数都能表示成两个整数之比.其中说法正确的是
.(填序号)
14.已知x是的整数部分,y是的小数部分,则xy的值
.
15.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为
.
16.如图,将一副三角板按如图放置,则下列结论:
①∠1=∠3;
②如果∠2=30°,则有BC∥AE;
③如果∠1=∠2=∠3,则有BC∥AE;
④如果∠2=45°,必有∠4=∠E.其中正确的有
(填序号).
17.三个同学对问题“若方程组,的解是,求方程组的解.”提出各自的想法:甲说:“这个题目好象条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“可以把第二个方程组的两个方程的两边都除以7,通过换元替换的方法来解决.”参考他们的讨论,你认为这题目的解应该是:
.
18.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
°.
三.解答题(共8小题,满分66分)
19.(6分)计算:
(1)﹣|2﹣|﹣+2;
(2)3﹣|﹣|.
20.(6分)解方组:
(1);
(2).
21.(8分)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
22.(8分)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
23.(9分)某环卫公司通过政府采购的方式计划购进一批A,B两种型号的新能源汽车.据了解,2辆A型汽车和3辆B型汽车的进价共计80万元;3辆A型汽车和2辆B型汽车的进价共计95万元.
(1)求A,B两种型号的汽车每辆进价分别为多少万元;
(2)该公司计划恰好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),并使得购进的B种型号的新能源汽车数量多于A种型号的新能源汽车数量,请直接写出该公司的采购方案.
24.(9分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
25.(10分)已知关于x,y的二元一次方程组的解x与y的值互为相反数,试求m的值和方程组的解.
26.(10分)如图①,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系;(不用证明)
(2)如图②,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图③,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC所夹的锐角的度数吗?如果能,请直接写出这个锐角的度数;如果不能,请说明理由.
2021年02月15日宫老师的初中数学平行组卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、﹣y+xy=2,是二元二次方程,不合题意;
B、3x﹣11=5x,是一元一次方程,不合题意;
C、3x=2+y,是二元一次方程,符合题意;
D、﹣=,是分式方程,不合题意;
故选:C.
2.解:由正数的两个平方根互为相反数可得
(2x﹣3)+(5﹣x)=0,
解得x=﹣2,
所以5﹣x=5﹣(﹣2)=7,
所以a=72=49.
故选:B.
3.解:A、+0.3>﹣0.1,故本选项不符合题意;
B、0>﹣|﹣7|,故本选项不符合题意;
C、∵1.4142=1.999396,
∴﹣<﹣1.414,故本选项符合题意;
D、﹣<﹣,故本选项不符合题意;
故选:C.
4.解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
故选:D.
5.解:∵DE∥AB
∴∠A=∠CED=60°,
∵DM∥AC
∴∠DMF=∠A=60°,
∵DF⊥AB
∠DFM=90°,
∴∠MDF=90°﹣60°=30°.
故选:C.
6.解:A、在同一平面内,两条直线的位置只有两种:相交和平行,垂直是相交的一种情况,故A错误;
B、点到直线的距离指的是线段的长度,而非垂线段,故B错误;
C、两直线平行,同旁内角互补,故C错误;
D、两点之间线段最短,故D正确.
故选:D.
7.解:∵点P(t+3,t+2)在直角坐标系的x轴上,
∴t+2=0,
解得:t=﹣2,
故t+3=1,
则P点坐标为(1,0).
故选:D.
8.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
9.解:∵点P(3a,a+2)在x轴上,
∴y=0,
即a+2=0,
解得a=﹣2,
∴3a=﹣6,
∴点P的坐标为(﹣6,0).
故选:C.
10.解:依题意得:.
故选:C.
11.解:①将a=1代入原方程组,得解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
若x,y是互为相反数,则x+y=0,
即2a+1+2﹣2a=0,方程无解.
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
12.解:如图,
∵∠APE=∠CQE,
∴AB∥CD,
∴∠BPQ+∠DQP=180°,
∵PM平分∠BPQ,QN平分∠DQP,
∴∠BPQ=2∠MPQ,∠DQP=2∠NQP,
∴∠MPQ+∠NQP=90°,
∴∠POQ=90°,
即PM⊥QN,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
13.解:①任何有限小数或无限循环小数都是有理数,正确;
②无限不循环小数是无理数,正确;
③无理数都是无限小数,正确;
④有理数包括整数和分数,整数可以表示为整数:1的形式,分数本身就是分子:分母的形式,正确.
故答案为:①②③④.
14.解:∵x是的整数部分,
∴x=2,
∵y是的小数部分,
∴y=﹣2,
∴yx=2(﹣2)=2﹣4,
故答案为2﹣4.
15.解:将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
16.解:∵∠EAD=∠CAB=90°,
∴∠1=∠3,故①正确,
当∠2=30°时,∠3=60°,∠4=45°,
∴∠3≠∠4,
故AE与BC不平行,故②错误,
当∠1=∠2=∠3时,可得∠3=∠4=45°,
∴BC∥AE,故③正确,
∵∠E=60°,∠4=45°,
∴∠E≠∠4,故④错误,
故答案为:①③.
17.解:,
两边同时除以7得,
,
∵方程组的解是,
∴,
解得:;
故答案为:.
18.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=92°,
∴∠CFE=92°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣92°=23°.
故答案为:23.
三.解答题(共8小题,满分66分)
19.解:(1)﹣|2﹣|﹣+2
=﹣4﹣+2﹣3+2
=﹣5.
(2)3﹣|﹣|
=3﹣+
=4﹣.
20.解:,
②×3﹣①×2,得11x=﹣15,解得x=﹣,
把x=﹣代入①,得,解得y=,
故原方程组的解为;
(2)原方程组可化为,
①﹣②,得4y=8,解得y=2,
把y=2代入②,得2x﹣2=4,解得x=3,
故方程组的解为.
21.解:(1)C(0,2),D(4,2)
S四边形ABDC=AB?OC=4×2=8;
(2)存在,当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
22.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
23.解:(1)设A型汽车每辆的进价为x万元,B型汽车每辆的进价为y万元,
依题意,得:,
解得:,
答:A型汽车每辆的进价为25万元,B型汽车每辆的进价为10万元.
(2)设购进A型汽车m辆,购进B型汽车n辆,m<n,
依题意,得:25m+10n=200,
∴m=8﹣n.
∵m,n均为正整数,
∴n为5的倍数,
∴或或,
∵m<n,
∴不合题意舍去,
∴共2种购买方案,
方案一:购进A型车4辆,B型车10辆;
方案二:购进A型车2辆,B型车15辆.
24.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
25.解:方程组,
②×2+①得7x=5m+1,
∴x=,
将x=代入②,得y=,
∵x与y的值互为相反数,
∴+=0
∴m=﹣10,
∴x=﹣7,y=7,
∴原方程组的解为.
26.解:(1)结论:BD=AC,BD⊥AC.
理由:延长BD交AC于F.
∵AE⊥CB
∴∠AEC=∠BED=90°.
在△AEC和△BED中,
,
∴△AEC≌△BED,
∴AC=BD,∠CAE=∠EBD,
∵∠AEC=90°,
∴∠C+∠CAE=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴AC⊥BD.
(2)如图2中,不发生变化,设DE与AC交于点O,BD与AC交于点F.
理由是:∵∠BEA=∠DEC=90°,∴∠BEA+∠AED=∠DEC+∠AED,∴∠BED=∠AEC,
在△BED和△AEC中,
,
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,
∵∠DEC=90°,
∴∠ACE+∠EOC=90°,
∵∠EOC=∠DOF,
∴∠BDE+∠DOF=90°,
∴∠DFO=180°﹣90°=90°,
∴BD⊥AC;
(3)①如图3中,结论:BD=AC,
理由是:∵△ABE和△DEC是等边三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
,
∴△BED≌△AEC,
∴BD=AC.
②能;设BD与AC交于点F,由△BED≌△AEC可知,∠BDE=∠ACE,
∴∠DFC=180°﹣(∠BDE+∠EDC+∠DCF)=180°﹣(∠ACE+∠EDC+∠DCF)=180°﹣(60°+60°)=60°,
即BD与AC所成的锐角的度数为60°.
同课章节目录
