人教版八年级数学下册课件-18.2.3 正方形(15张)
文档属性
| 名称 | 人教版八年级数学下册课件-18.2.3 正方形(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览


文档简介
正方形
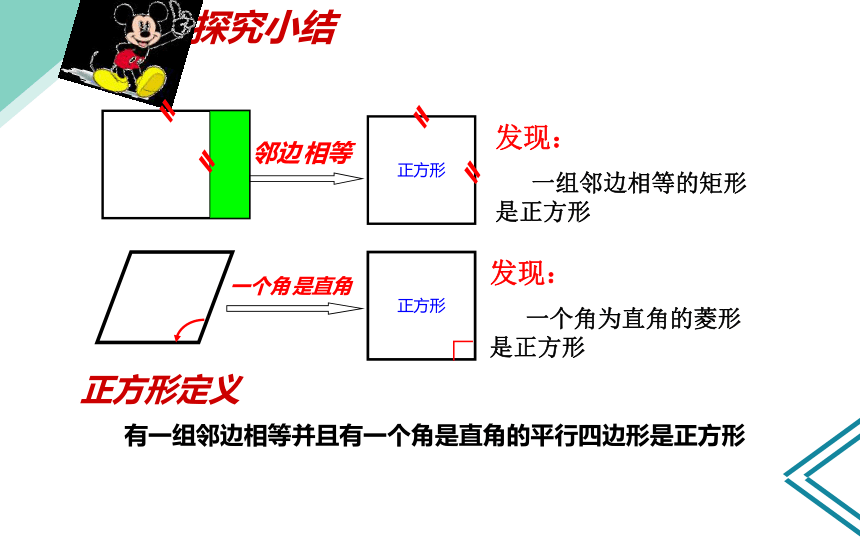
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
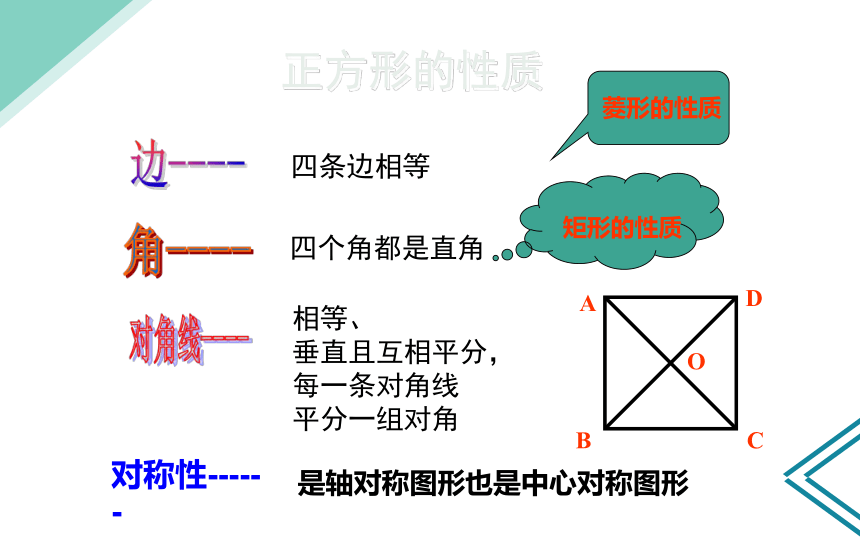
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
菱形的性质
矩形的性质
对称性------
是轴对称图形也是中心对称图形
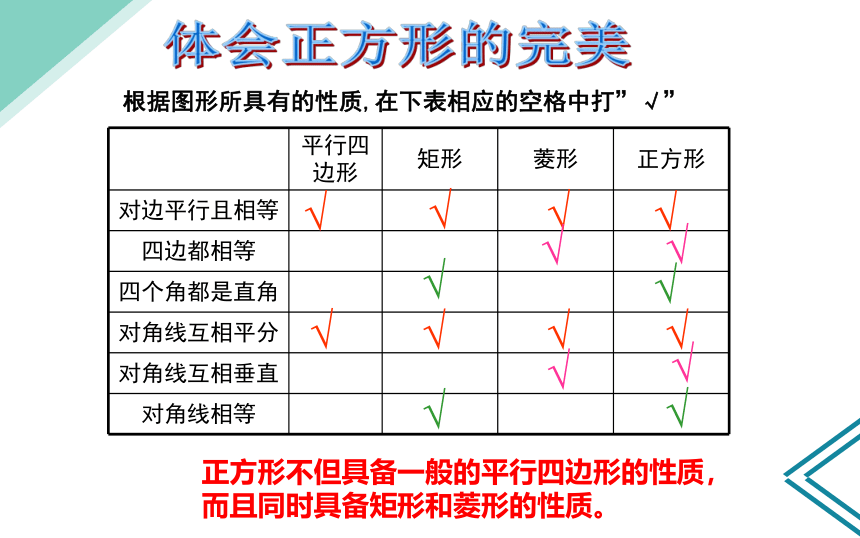
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
体会正方形的完美
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。
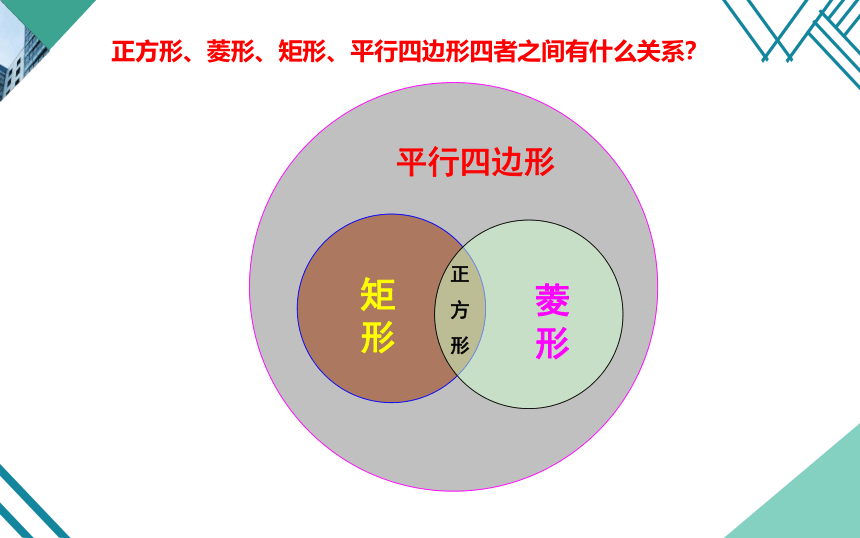
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
随堂小测验
下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( )
②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( )
④四条边都相等的四边形是正方形;( )
⑤四个角相等的四边形是正方形.( )
例
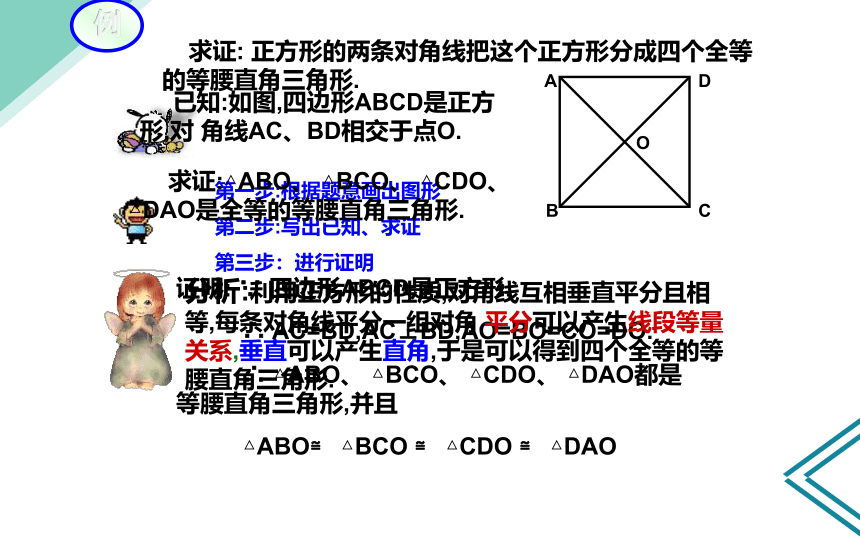
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做?你会做吗?
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
随堂练习
P59练习1、2
练习1 提示:有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
裁
练习2
提示:寻找直角三角形,运用直角三角形求边长和对角线.
.2.四边形ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积
和对角线长分别是多少?
A
D
A
B
C
E
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=30m,EB=10m
∴ S正方形ABCD=BC2=800(m2)
∴
∴
补充例1 已知:如图,正方形ABCD中,
对角线的交点为O,E是OB上的一点, DG⊥AE于G,DG交OA于F.
求证:OE=OF.
(补充例2 )已知:如图,四边形ABCD是正方形,分别过点A、C两点作直线L1∥L2,作BM⊥L1于M,DN⊥L1于N,直线MB、DN分别交
L1 、L2于Q、P点.
求证:四边形PQMN是正方形.
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质?
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
谢谢
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
菱形的性质
矩形的性质
对称性------
是轴对称图形也是中心对称图形
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
体会正方形的完美
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
随堂小测验
下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( )
②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( )
④四条边都相等的四边形是正方形;( )
⑤四个角相等的四边形是正方形.( )
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做?你会做吗?
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
随堂练习
P59练习1、2
练习1 提示:有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
裁
练习2
提示:寻找直角三角形,运用直角三角形求边长和对角线.
.2.四边形ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积
和对角线长分别是多少?
A
D
A
B
C
E
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=30m,EB=10m
∴ S正方形ABCD=BC2=800(m2)
∴
∴
补充例1 已知:如图,正方形ABCD中,
对角线的交点为O,E是OB上的一点, DG⊥AE于G,DG交OA于F.
求证:OE=OF.
(补充例2 )已知:如图,四边形ABCD是正方形,分别过点A、C两点作直线L1∥L2,作BM⊥L1于M,DN⊥L1于N,直线MB、DN分别交
L1 、L2于Q、P点.
求证:四边形PQMN是正方形.
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质?
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
谢谢
