人教版八年级数学下册 19.1.2 函数的图象 课件(17张)
文档属性
| 名称 | 人教版八年级数学下册 19.1.2 函数的图象 课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 00:00:00 | ||
图片预览




文档简介
一天中人的体温是随着时间的变化而变化的
19.1.2 函数的图像
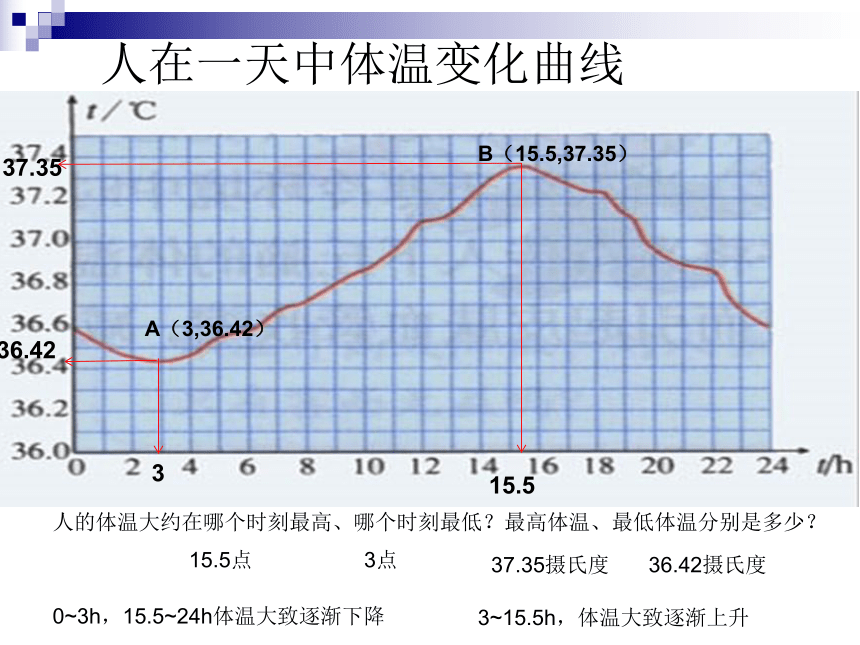
人在一天中体温变化曲线
人的体温大约在哪个时刻最高、哪个时刻最低?最高体温、最低体温分别是多少?
0~3h,15.5~24h体温大致逐渐下降
3点
36.42摄氏度
15.5点
37.35摄氏度
3~15.5h,体温大致逐渐上升
A(3,36.42)
B(15.5,37.35)
15.5
3
36.42
37.35
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
通过图象,我们可以数形结合地研究函数.
讲授新课
A(3,36.42)
B(15.5,37.35)
T/
O
1
时间
水位高度
1
2
3
4
5
4
3
2
5
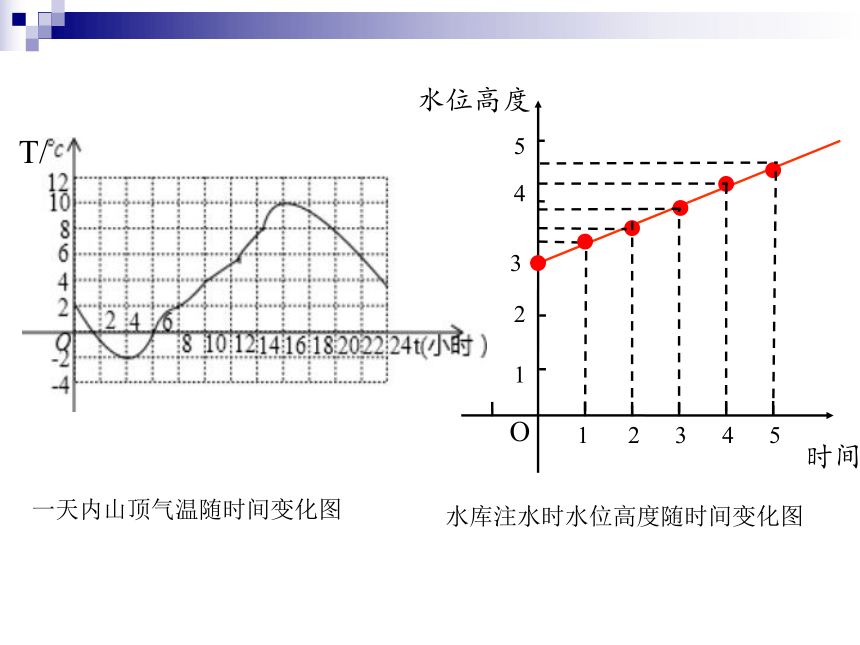
水库注水时水位高度随时间变化图
一天内山顶气温随时间变化图
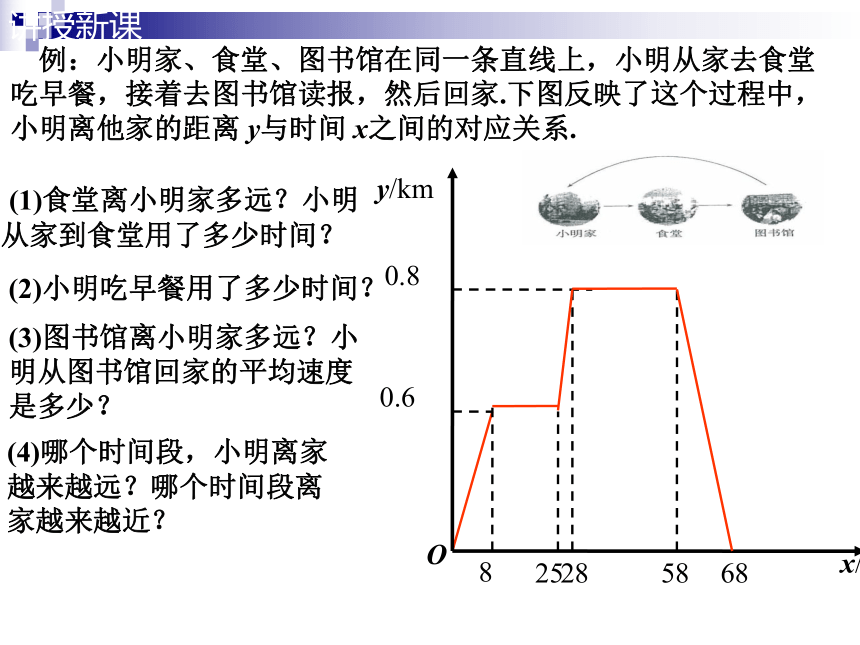
例:小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离他家的距离 y与时间 x之间的对应关系.
y/km
O
8
25
28
58
68
x/min
0.6
0.8
讲授新课
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)小明吃早餐用了多少时间?
(4)哪个时间段,小明离家越来越远?哪个时间段离家越来越近?
(3)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
归纳
1、看轴 明确变量
2、看线 变化趋势
3、看点 对应值
画出反映正方形面积S与边长X之间的函数关系图像
画一画!
S=????????
?
函数关系式:
(x>0)
(1)填写下表:
用空心圈表示不在曲线的点
用平滑曲线去连接画出的点
x
0.5
1
1.5
2
2.5
3
3.5
0.25
1
2.25
4
6.25
9
12.25
…
…
…
…
强化训练
画出这些函数的图象
(1)y=x+0.5;
(1)解:1.列表.
x
…
-3
-2
-1
0
1
2
3
…
y=x+0.5
…
…
2.描点.
3.连线.
O
-1
1
x
y
y=x+0.5
直线由左向右上升,即当x由小变大时,y=x+5随之增大.
-2.5
-0.5
0.5
1.5
2.5
3.5
-1.5
1
-1
强化训练
(2)解:1.列表.
x
1
2
3
4
6
…
…
2.描点.
3.连线.
曲线 从左向右下降,即当x由小变大时,随之减小.
6
3
2
1.5
1
强化训练
练习 : 八年级(7)班到某景点秋游,速度为每小时a千米,走了一段时间后,休息了一会,因道路变陡,又以每小时b千米(0A
B
C
D
A
O
小时
千米
O
O
O
千米
千米
千米
小时
小时
小时
判断点A(-2.5,-4)B(1,3)C(2.5,4)是否在函数 的图像上
????=2?????1
?
练习:
已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
(2)求当x=-4,-2,4时y的值是多少?
(3)求当y=0,4时x的值是多少?
(4)当x取何值时y的值最大?
当x取何值时y的值最小?
(5)当x的值在什么范围内时
y随x的增大而增大?当x的
值在什么范围内时y随x的
增大而减小?
(1)函数图象会使函数关系更为清晰,怎样画出函数的图象呢?
(2)你认为观察函数图象时要注意哪些问题?
课堂小结
图象信息(形)
图象上点的坐标特点(数)
对应关系和变化规律
谢谢观看!
19.1.2 函数的图像
人在一天中体温变化曲线
人的体温大约在哪个时刻最高、哪个时刻最低?最高体温、最低体温分别是多少?
0~3h,15.5~24h体温大致逐渐下降
3点
36.42摄氏度
15.5点
37.35摄氏度
3~15.5h,体温大致逐渐上升
A(3,36.42)
B(15.5,37.35)
15.5
3
36.42
37.35
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
通过图象,我们可以数形结合地研究函数.
讲授新课
A(3,36.42)
B(15.5,37.35)
T/
O
1
时间
水位高度
1
2
3
4
5
4
3
2
5
水库注水时水位高度随时间变化图
一天内山顶气温随时间变化图
例:小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离他家的距离 y与时间 x之间的对应关系.
y/km
O
8
25
28
58
68
x/min
0.6
0.8
讲授新课
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)小明吃早餐用了多少时间?
(4)哪个时间段,小明离家越来越远?哪个时间段离家越来越近?
(3)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
归纳
1、看轴 明确变量
2、看线 变化趋势
3、看点 对应值
画出反映正方形面积S与边长X之间的函数关系图像
画一画!
S=????????
?
函数关系式:
(x>0)
(1)填写下表:
用空心圈表示不在曲线的点
用平滑曲线去连接画出的点
x
0.5
1
1.5
2
2.5
3
3.5
0.25
1
2.25
4
6.25
9
12.25
…
…
…
…
强化训练
画出这些函数的图象
(1)y=x+0.5;
(1)解:1.列表.
x
…
-3
-2
-1
0
1
2
3
…
y=x+0.5
…
…
2.描点.
3.连线.
O
-1
1
x
y
y=x+0.5
直线由左向右上升,即当x由小变大时,y=x+5随之增大.
-2.5
-0.5
0.5
1.5
2.5
3.5
-1.5
1
-1
强化训练
(2)解:1.列表.
x
1
2
3
4
6
…
…
2.描点.
3.连线.
曲线 从左向右下降,即当x由小变大时,随之减小.
6
3
2
1.5
1
强化训练
练习 : 八年级(7)班到某景点秋游,速度为每小时a千米,走了一段时间后,休息了一会,因道路变陡,又以每小时b千米(0
B
C
D
A
O
小时
千米
O
O
O
千米
千米
千米
小时
小时
小时
判断点A(-2.5,-4)B(1,3)C(2.5,4)是否在函数 的图像上
????=2?????1
?
练习:
已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
(2)求当x=-4,-2,4时y的值是多少?
(3)求当y=0,4时x的值是多少?
(4)当x取何值时y的值最大?
当x取何值时y的值最小?
(5)当x的值在什么范围内时
y随x的增大而增大?当x的
值在什么范围内时y随x的
增大而减小?
(1)函数图象会使函数关系更为清晰,怎样画出函数的图象呢?
(2)你认为观察函数图象时要注意哪些问题?
课堂小结
图象信息(形)
图象上点的坐标特点(数)
对应关系和变化规律
谢谢观看!
