人教版八年级数学下册 19.2.1 正比例函数 课件(24张)
文档属性
| 名称 | 人教版八年级数学下册 19.2.1 正比例函数 课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 15:52:46 | ||
图片预览








文档简介
正比例函数的图像和性质
目
录
Contents
温故知新
01
探索新知
02
应用新知
03
再探新知
04
05
归 纳 总 结
温故知新
01
问题1:下列函数哪些是正比例函数?
(1)y=-3x ; (2)y= x + 3;
(3)y= 4x; (4)y= x2.
(1) (3)
01
一般地,形如 y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
列表、描点、连线
正比例函数的定义
画函数图象的步骤
探索新知
02
02
现在我们已经知道了正比例函数y=kx(k ≠0)的定义和画图象的步骤,那么正比例函数的图象有什么特征呢?
02
v
v
v
k ≠0可分为k>0和k<0
分组画图讨论
(1) k>0:画函数y=2x 的图象
再画函数 的图象
( 2)k<0:画函数y=-2x 的图象
再 画函数 的图象
画正比例函数 y =kx (k≠0)的图象
02
解:
1.列表:
2.描点:
3.连线:
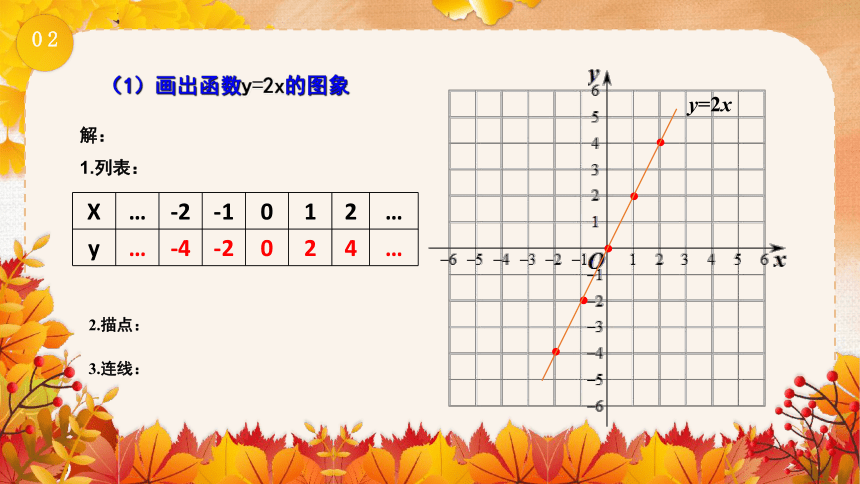
(1)画出函数y=2x的图象
X
…
-2
-1
0
1
2
…
y
…
-4
-2
0
2
4
…
y=2x
02
再画出函数 的图象
X
…
-4
-2
0
2
4
…
y
…
-2
-1
0
1
2
…
解:
1.列表:
2.描点:
3.连线:
-
-
-
-
-
5
4
3
2
1
-1 0
-2
-3
-4
-5
x
y
5
4
3
2
1
1
2
3
4
5
(k>0)
02
发现k>0两次画出的图象的相同点了吗?
当k>0时,函数图像有什么共同特征和性质?
①都是一条直线
②都过原点(0,0)
③ 图像过第一,三象限
④图像自左向右上升
⑤y随x的增大而增大
(2)画出函数y=-2x的图象
解:
1.列表
x
…
-2
-1
0
1
2
…
y
…
4
2
0
-2
-4
…
02
2.描点:
3.连线:
02
2.描点:
解:
1.列表:
3.连线:
X
…
-4
-2
0
2
4
…
y
…
2
1
0
-1
-2
…
再画出函数 的图象
02
5
4
3
2
1
1
2
3
4
5
(k<0)
-
-
-
-
-
5
4
3
2
1
-1 0
-2
-3
-4
-5
x
y
发现k<0两次画出的图象的相同点了吗?
当k<0时,函数图像有什么共同特征和性质?
①都是一条直线
②都过原点(0,0)
③ 图像过第二,四象限
④图像自左向右下降
⑤y随x的增大而减小
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
02
y=kx (k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx (k≠0)
y=kx
经过的象限
直线从左向右
Y随x的增大而
k>0
第三、一象限
上升
增大
k<0
第二、四象限
下降
减小
应用新知
03
03
1.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A. m =1 B. m>1
C. m<1 D. m≥1
分析:因为函数图象经过第一、三象限,所以m-1>0,解得m>1.
B
2.已知正比例函数y=kx(k<0)的图象上有两点(-3,y1),
(1,y2),则y1 y2.
分析:因为k<0,所以y的值随着x值的增大而减小,
又-3<1,则y1>y2.
03
>
再探新知
04
04
用最简便的方法画出下列函数的图象:
(1) y= x (2) y=-3x
两点
作图法
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
通过以上的学习,画正比例函数有无简便的方法呢?
04
(1)y= x (2)y=-3x
(1, )
-3
1
1
(1,-3)
2
1
x
y
x
y
y= x
y=-3x
0
0
归纳总结
05
23
正比例函数的图象和性质
图象:经过原点的直线.
当k>0时,经过第一、三象限;
当k<0时,经过第二、四象限.
性质:
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
05
正比例函数图象的简单作法:
过(0,0)和(1,K )作直线
感谢您的观看
目
录
Contents
温故知新
01
探索新知
02
应用新知
03
再探新知
04
05
归 纳 总 结
温故知新
01
问题1:下列函数哪些是正比例函数?
(1)y=-3x ; (2)y= x + 3;
(3)y= 4x; (4)y= x2.
(1) (3)
01
一般地,形如 y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
列表、描点、连线
正比例函数的定义
画函数图象的步骤
探索新知
02
02
现在我们已经知道了正比例函数y=kx(k ≠0)的定义和画图象的步骤,那么正比例函数的图象有什么特征呢?
02
v
v
v
k ≠0可分为k>0和k<0
分组画图讨论
(1) k>0:画函数y=2x 的图象
再画函数 的图象
( 2)k<0:画函数y=-2x 的图象
再 画函数 的图象
画正比例函数 y =kx (k≠0)的图象
02
解:
1.列表:
2.描点:
3.连线:
(1)画出函数y=2x的图象
X
…
-2
-1
0
1
2
…
y
…
-4
-2
0
2
4
…
y=2x
02
再画出函数 的图象
X
…
-4
-2
0
2
4
…
y
…
-2
-1
0
1
2
…
解:
1.列表:
2.描点:
3.连线:
-
-
-
-
-
5
4
3
2
1
-1 0
-2
-3
-4
-5
x
y
5
4
3
2
1
1
2
3
4
5
(k>0)
02
发现k>0两次画出的图象的相同点了吗?
当k>0时,函数图像有什么共同特征和性质?
①都是一条直线
②都过原点(0,0)
③ 图像过第一,三象限
④图像自左向右上升
⑤y随x的增大而增大
(2)画出函数y=-2x的图象
解:
1.列表
x
…
-2
-1
0
1
2
…
y
…
4
2
0
-2
-4
…
02
2.描点:
3.连线:
02
2.描点:
解:
1.列表:
3.连线:
X
…
-4
-2
0
2
4
…
y
…
2
1
0
-1
-2
…
再画出函数 的图象
02
5
4
3
2
1
1
2
3
4
5
(k<0)
-
-
-
-
-
5
4
3
2
1
-1 0
-2
-3
-4
-5
x
y
发现k<0两次画出的图象的相同点了吗?
当k<0时,函数图像有什么共同特征和性质?
①都是一条直线
②都过原点(0,0)
③ 图像过第二,四象限
④图像自左向右下降
⑤y随x的增大而减小
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
02
y=kx (k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx (k≠0)
y=kx
经过的象限
直线从左向右
Y随x的增大而
k>0
第三、一象限
上升
增大
k<0
第二、四象限
下降
减小
应用新知
03
03
1.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A. m =1 B. m>1
C. m<1 D. m≥1
分析:因为函数图象经过第一、三象限,所以m-1>0,解得m>1.
B
2.已知正比例函数y=kx(k<0)的图象上有两点(-3,y1),
(1,y2),则y1 y2.
分析:因为k<0,所以y的值随着x值的增大而减小,
又-3<1,则y1>y2.
03
>
再探新知
04
04
用最简便的方法画出下列函数的图象:
(1) y= x (2) y=-3x
两点
作图法
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
通过以上的学习,画正比例函数有无简便的方法呢?
04
(1)y= x (2)y=-3x
(1, )
-3
1
1
(1,-3)
2
1
x
y
x
y
y= x
y=-3x
0
0
归纳总结
05
23
正比例函数的图象和性质
图象:经过原点的直线.
当k>0时,经过第一、三象限;
当k<0时,经过第二、四象限.
性质:
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
05
正比例函数图象的简单作法:
过(0,0)和(1,K )作直线
感谢您的观看
