人教版数学七年级下册 7.2坐标方法的简单应用随堂练习(Word版 含答案)
文档属性
| 名称 | 人教版数学七年级下册 7.2坐标方法的简单应用随堂练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 739.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 16:02:37 | ||
图片预览



文档简介
人教版数学七年级下7.2坐标方法的简单应用随堂练习
一、选择题(共12小题;共60分)
1.
如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点
,,则“宝藏”点
的位置是
A.
B.
C.
D.
2.
如果点
在直线
上,点
的坐标是
,点
的坐标是
,那么三角形
的面积
A.
等于
B.
大于
C.
小于
D.
无法确定
3.
在平面直角坐标系中,点
的坐标变为
,则点
经历了怎样的图形变化
A.
先向左平移
个单位长度,再向下平移
个单位长度
B.
先向左平移
个单位长度,再向上平移
个单位长度
C.
先向右平移
个单位长度,再向上平移
个单位长度
D.
先向右平移
个单位长度,再向下平移
个单位长度
4.
如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为
,黑棋(乙)的坐标为
,则白棋(甲)的坐标是
A.
B.
C.
D.
5.
如图,,,
的坐标分别为:,,,在线段
或线段
上找一点
使
面积为整数且
,则满足条件的点
的个数是
A.
B.
C.
D.
6.
在平面直角坐标系中,将点
向右平移
个单位长度得到点
,则点
关于
轴的对称点
的坐标是
A.
B.
C.
D.
7.
如图,在一次活动中,位于
处的七年一班准备前往相距
的
与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为
A.
南偏西
,
B.
南偏西
,
C.
北偏东
,
D.
北偏东
,
8.
在平面直角坐标系中,点
的坐标变为
,则点
经历了怎样的图形变化
A.
先向左平移
个单位长度,再向下平移
个单位长度
B.
先向左平移
个单位长度,再向上平移
个单位长度
C.
先向右平移
个单位长度,再向上平移
个单位长度
D.
先向右平移
个单位长度,再向下平移
个单位长度
9.
已知点
,且
,点
到
轴的距离是
个单位,到
轴的距离是
个单位,则点
的坐标是
A.
B.
C.
或
D.
10.
在平面直角坐标系中,将点
向右平移
个单位长度,再向下平移
个单位长度所得到的点坐标为
A.
B.
C.
D.
11.
如图,在平面直角坐标系内放置一个直角梯形
,已知
,,,若点
在梯形内,且
,,那么点
的坐标是
A.
B.
C.
D.
12.
如图所示,四边形
中,,,,设
的长为
,四边形
的面积为
,则
与
之间的函数关系式是
A.
B.
C.
D.
二、填空题(共5小题;共25分)
13.
在平面直角坐标系中,将点
向右平移
个单位长度,再向下平移
个单位长度,那么平移后对应的点
的坐标为
?.
14.
将点
先向下平移
个单位长度,在向左平移
个单位长度,得到点
,则点
的坐标是
?.
15.
平面直角坐标系中有一点
在第四象限,它到
轴的距离是
,到
轴的距离是
,则点
的坐标为
?.
16.
平面直角坐标系中有一点
在第四象限,它到
轴的距离是
,到
轴的距离是
,则点
的坐标为
?.
17.
如果直线
与两坐标轴所围成的三角形面积是
,则
的值为
?.
三、解答题(共5小题;共65分)
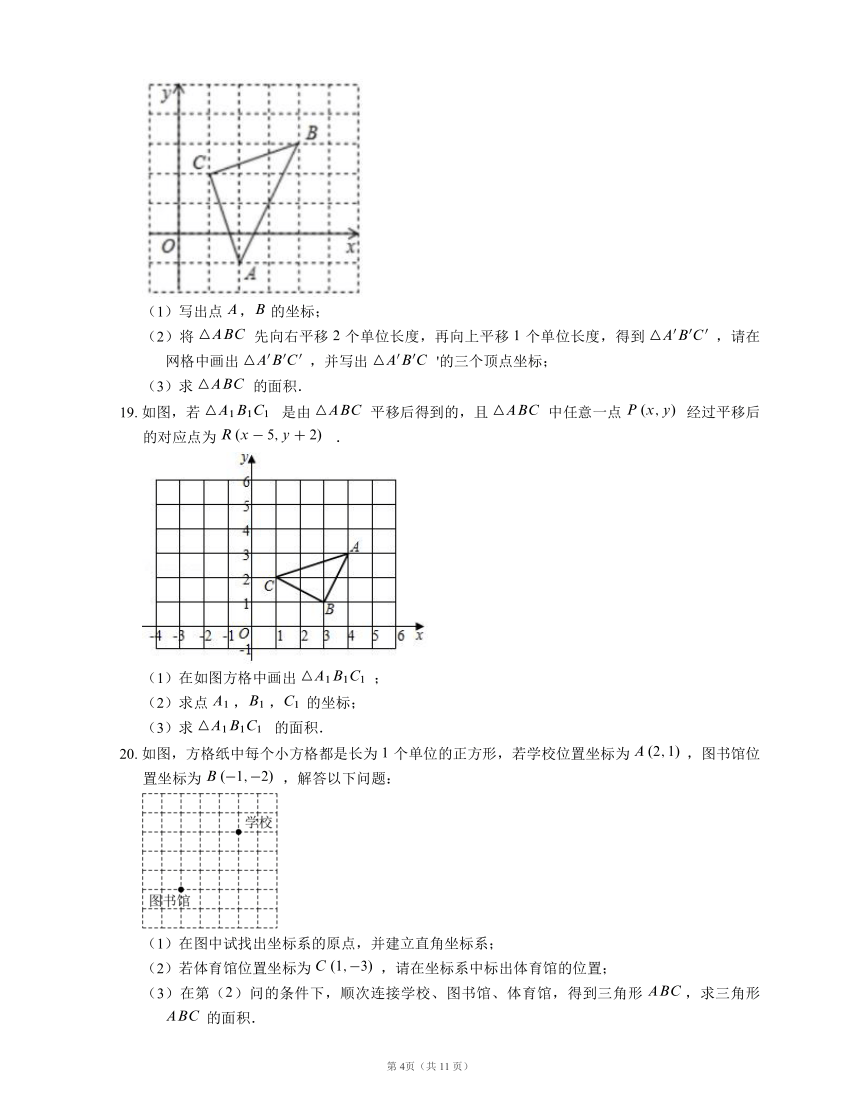
18.
如图,直角坐标系中,
的顶点都在网格点上,其中,
点坐标为
.
(1)写出点
,
的坐标;
(2)将
先向右平移
个单位长度,再向上平移
个单位长度,得到
,请在网格中画出
,并写出
'的三个顶点坐标;
(3)求
的面积.
19.
如图,若
是由
平移后得到的,且
中任意一点
经过平移后的对应点为
.
(1)在如图方格中画出
;
(2)求点
,,
的坐标;
(3)求
的面积.
20.
如图,方格纸中每个小方格都是长为
个单位的正方形,若学校位置坐标为
,图书馆位置坐标为
,解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为
,请在坐标系中标出体育馆的位置;
(3)在第()问的条件下,顺次连接学校、图书馆、体育馆,得到三角形
,求三角形
的面积.
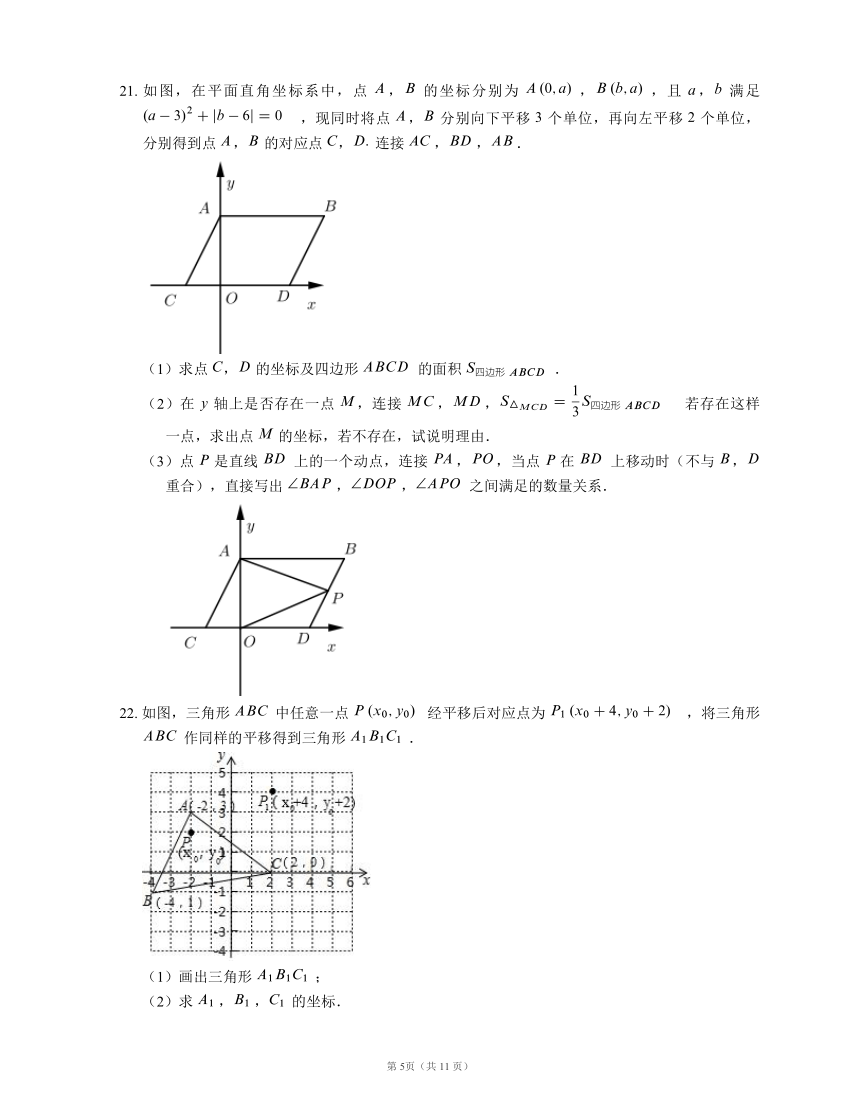
21.
如图,在平面直角坐标系中,点
,
的坐标分别为
,,且
,
满足
,现同时将点
,
分别向下平移
个单位,再向左平移
个单位,分别得到点
,
的对应点
,
连接
,,.
(1)求点
,
的坐标及四边形
的面积
.
(2)在
轴上是否存在一点
,连接
,,
若存在这样一点,求出点
的坐标,若不存在,试说明理由.
(3)点
是直线
上的一个动点,连接
,,当点
在
上移动时(不与
,
重合),直接写出
,,
之间满足的数量关系.
22.
如图,三角形
中任意一点
经平移后对应点为
,将三角形
作同样的平移得到三角形
.
(1)画出三角形
;
(2)求
,,
的坐标.
答案
第一部分
1.
D
【解析】由
,
点坐标可知坐标系,
则知
点坐标为
.
2.
A
3.
A
4.
D
【解析】根据题意可建立如图所示平面直角坐标系:
由坐标系知白棋(甲)的坐标是
,
故选:D.
5.
C
【解析】由题意得:,
,
.
又
点在线段
或线段
上,
满足条件的
的个数为:.
6.
D
【解析】将点
向右平移
个单位长度得到点
坐标为
,
点
关于
轴的对称点
的坐标是
.
7.
B
8.
A
【解析】
在平面直角坐标系中,点
的坐标变为
,
点
的横坐标减少
,纵坐标减少
,
点
先向左平移
个单位长度,再向下平移
个单位长度.
故选:A.
9.
C
【解析】,
,
同号,
点
到
轴的距离是
个单位,到
轴的距离是
个单位,
点
的横坐标是
或
,纵坐标是
或
,
点
的坐标是
或
.
10.
D
【解析】将点
向右平移
个单位长度,到达点坐标为
,再向下平移
个单位长度所得到的点坐标为
.
11.
B
【解析】设
点的纵坐标是
,
因而根据
,得到
,
解得
,因而
点的纵坐标是
;
设
的横坐标是
,则
的面积是
,
过
作
,交
,
分别于
,,
的面积是
,
根据
,得到
,因而点
的坐标是
.
12.
C
第二部分
13.
14.
【解析】
点
先向下平移
个单位长度,在向左平移
个单位长度得到点
,
点
的横坐标为
,
纵坐标为
,
点
的坐标为
.
15.
【解析】
在第四象限,
点横坐标为正数,纵坐标为负数.
它到
轴的距离是
,
纵坐标为
,
到
轴的距离是
,
横坐标为
.
点坐标为
.
16.
【解析】
点
在第四象限,
其横、纵坐标分别为正数、负数,
点
到
轴的距离为
,到
轴的距离为
,
点
的坐标为
.
17.
第三部分
18.
(1)
,;
??????(2)
如图,
为所作;,,;
??????(3)
的面积
.
19.
(1)
如图,
为所作;
??????(2)
点
的坐标为
,点
的坐标为
,点
的坐标为
;
??????(3)
的面积
.
20.
(1)
如图,
??????(2)
如图,
??????(3)
.
21.
(1)
,
,,解得
,,
,,
将点
,
分别向下平移
个单位,再向左平移
个单位,分别得到点
,
的对应点
,.
,,
.
??????(2)
在
轴上存在一点
,使
,
设
的坐标为
,
,
,解得
,
.
??????(3)
①
;
②
;
③
.
【解析】①当点
在线段
上移动时,,
理由如下:
如图
,过点
作
,
由
平移得到,则
,
,
,,
,
②当点
在
的延长线上时,同①的方法得,,
③当点
在
的延长线上时,同①的方法得,.
22.
(1)
如图,
即为所求.
??????(2)
由题可得,三角形向右平移
个单位、向上平移
个单位,
,,.
第1页(共1
页)
一、选择题(共12小题;共60分)
1.
如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点
,,则“宝藏”点
的位置是
A.
B.
C.
D.
2.
如果点
在直线
上,点
的坐标是
,点
的坐标是
,那么三角形
的面积
A.
等于
B.
大于
C.
小于
D.
无法确定
3.
在平面直角坐标系中,点
的坐标变为
,则点
经历了怎样的图形变化
A.
先向左平移
个单位长度,再向下平移
个单位长度
B.
先向左平移
个单位长度,再向上平移
个单位长度
C.
先向右平移
个单位长度,再向上平移
个单位长度
D.
先向右平移
个单位长度,再向下平移
个单位长度
4.
如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为
,黑棋(乙)的坐标为
,则白棋(甲)的坐标是
A.
B.
C.
D.
5.
如图,,,
的坐标分别为:,,,在线段
或线段
上找一点
使
面积为整数且
,则满足条件的点
的个数是
A.
B.
C.
D.
6.
在平面直角坐标系中,将点
向右平移
个单位长度得到点
,则点
关于
轴的对称点
的坐标是
A.
B.
C.
D.
7.
如图,在一次活动中,位于
处的七年一班准备前往相距
的
与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为
A.
南偏西
,
B.
南偏西
,
C.
北偏东
,
D.
北偏东
,
8.
在平面直角坐标系中,点
的坐标变为
,则点
经历了怎样的图形变化
A.
先向左平移
个单位长度,再向下平移
个单位长度
B.
先向左平移
个单位长度,再向上平移
个单位长度
C.
先向右平移
个单位长度,再向上平移
个单位长度
D.
先向右平移
个单位长度,再向下平移
个单位长度
9.
已知点
,且
,点
到
轴的距离是
个单位,到
轴的距离是
个单位,则点
的坐标是
A.
B.
C.
或
D.
10.
在平面直角坐标系中,将点
向右平移
个单位长度,再向下平移
个单位长度所得到的点坐标为
A.
B.
C.
D.
11.
如图,在平面直角坐标系内放置一个直角梯形
,已知
,,,若点
在梯形内,且
,,那么点
的坐标是
A.
B.
C.
D.
12.
如图所示,四边形
中,,,,设
的长为
,四边形
的面积为
,则
与
之间的函数关系式是
A.
B.
C.
D.
二、填空题(共5小题;共25分)
13.
在平面直角坐标系中,将点
向右平移
个单位长度,再向下平移
个单位长度,那么平移后对应的点
的坐标为
?.
14.
将点
先向下平移
个单位长度,在向左平移
个单位长度,得到点
,则点
的坐标是
?.
15.
平面直角坐标系中有一点
在第四象限,它到
轴的距离是
,到
轴的距离是
,则点
的坐标为
?.
16.
平面直角坐标系中有一点
在第四象限,它到
轴的距离是
,到
轴的距离是
,则点
的坐标为
?.
17.
如果直线
与两坐标轴所围成的三角形面积是
,则
的值为
?.
三、解答题(共5小题;共65分)
18.
如图,直角坐标系中,
的顶点都在网格点上,其中,
点坐标为
.
(1)写出点
,
的坐标;
(2)将
先向右平移
个单位长度,再向上平移
个单位长度,得到
,请在网格中画出
,并写出
'的三个顶点坐标;
(3)求
的面积.
19.
如图,若
是由
平移后得到的,且
中任意一点
经过平移后的对应点为
.
(1)在如图方格中画出
;
(2)求点
,,
的坐标;
(3)求
的面积.
20.
如图,方格纸中每个小方格都是长为
个单位的正方形,若学校位置坐标为
,图书馆位置坐标为
,解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为
,请在坐标系中标出体育馆的位置;
(3)在第()问的条件下,顺次连接学校、图书馆、体育馆,得到三角形
,求三角形
的面积.
21.
如图,在平面直角坐标系中,点
,
的坐标分别为
,,且
,
满足
,现同时将点
,
分别向下平移
个单位,再向左平移
个单位,分别得到点
,
的对应点
,
连接
,,.
(1)求点
,
的坐标及四边形
的面积
.
(2)在
轴上是否存在一点
,连接
,,
若存在这样一点,求出点
的坐标,若不存在,试说明理由.
(3)点
是直线
上的一个动点,连接
,,当点
在
上移动时(不与
,
重合),直接写出
,,
之间满足的数量关系.
22.
如图,三角形
中任意一点
经平移后对应点为
,将三角形
作同样的平移得到三角形
.
(1)画出三角形
;
(2)求
,,
的坐标.
答案
第一部分
1.
D
【解析】由
,
点坐标可知坐标系,
则知
点坐标为
.
2.
A
3.
A
4.
D
【解析】根据题意可建立如图所示平面直角坐标系:
由坐标系知白棋(甲)的坐标是
,
故选:D.
5.
C
【解析】由题意得:,
,
.
又
点在线段
或线段
上,
满足条件的
的个数为:.
6.
D
【解析】将点
向右平移
个单位长度得到点
坐标为
,
点
关于
轴的对称点
的坐标是
.
7.
B
8.
A
【解析】
在平面直角坐标系中,点
的坐标变为
,
点
的横坐标减少
,纵坐标减少
,
点
先向左平移
个单位长度,再向下平移
个单位长度.
故选:A.
9.
C
【解析】,
,
同号,
点
到
轴的距离是
个单位,到
轴的距离是
个单位,
点
的横坐标是
或
,纵坐标是
或
,
点
的坐标是
或
.
10.
D
【解析】将点
向右平移
个单位长度,到达点坐标为
,再向下平移
个单位长度所得到的点坐标为
.
11.
B
【解析】设
点的纵坐标是
,
因而根据
,得到
,
解得
,因而
点的纵坐标是
;
设
的横坐标是
,则
的面积是
,
过
作
,交
,
分别于
,,
的面积是
,
根据
,得到
,因而点
的坐标是
.
12.
C
第二部分
13.
14.
【解析】
点
先向下平移
个单位长度,在向左平移
个单位长度得到点
,
点
的横坐标为
,
纵坐标为
,
点
的坐标为
.
15.
【解析】
在第四象限,
点横坐标为正数,纵坐标为负数.
它到
轴的距离是
,
纵坐标为
,
到
轴的距离是
,
横坐标为
.
点坐标为
.
16.
【解析】
点
在第四象限,
其横、纵坐标分别为正数、负数,
点
到
轴的距离为
,到
轴的距离为
,
点
的坐标为
.
17.
第三部分
18.
(1)
,;
??????(2)
如图,
为所作;,,;
??????(3)
的面积
.
19.
(1)
如图,
为所作;
??????(2)
点
的坐标为
,点
的坐标为
,点
的坐标为
;
??????(3)
的面积
.
20.
(1)
如图,
??????(2)
如图,
??????(3)
.
21.
(1)
,
,,解得
,,
,,
将点
,
分别向下平移
个单位,再向左平移
个单位,分别得到点
,
的对应点
,.
,,
.
??????(2)
在
轴上存在一点
,使
,
设
的坐标为
,
,
,解得
,
.
??????(3)
①
;
②
;
③
.
【解析】①当点
在线段
上移动时,,
理由如下:
如图
,过点
作
,
由
平移得到,则
,
,
,,
,
②当点
在
的延长线上时,同①的方法得,,
③当点
在
的延长线上时,同①的方法得,.
22.
(1)
如图,
即为所求.
??????(2)
由题可得,三角形向右平移
个单位、向上平移
个单位,
,,.
第1页(共1
页)
