2020-2021学年八年级数学人教版下册18.2.3 正方形同步练习(Word版 无答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.2.3 正方形同步练习(Word版 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 288.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 16:06:44 | ||
图片预览


文档简介
18.2.3
正方形
一、选择题
1、已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件即可推出该四边形是正方形,那么这个条件可以是(
)
A、∠D=90°
B、AB=CD
C、AD=BC
D、BC=CD
如图,在正方形ABCD中,对角线AC、BD相交于点O,则图中的等腰三角形有(
)
A、4个
B、6个
C、8个
D、10个
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是(
)
BE=AF
B、∠DAF=∠BEC
C、∠AFB+∠BEC=90°
D、AG⊥BE
在四边形ABCD中,O四对角线的交点,能判定这个四边形是正方形的条件是(
)
AC=BD,ABCD
B、AD//BC,∠A=∠C
C、AO=BO=CO=DO,AC⊥BD
D、AO=CO,BO=DO,AB=BC,AB=BC
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE:EC=2:1,则线段CH的长是(
)。
3
B、4
C、5
D、6
在
ABCD中,下列条件不能判断ABCD是正方形的是(
)
∠ABC=90°且AB=AD
B、AB=BC且AC⊥BD
C、AC⊥BD且AC=BD
D、AC=BD
且AB=BC
如图,正方形ABCD的面积是1,则以相邻两边中点连线EF为边的正方形EFGH的周长为(
)
B、2
C、+1
D、2+1
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长度为2,则FM的长为(
)
A、2
B、
C、
D、1
填空题
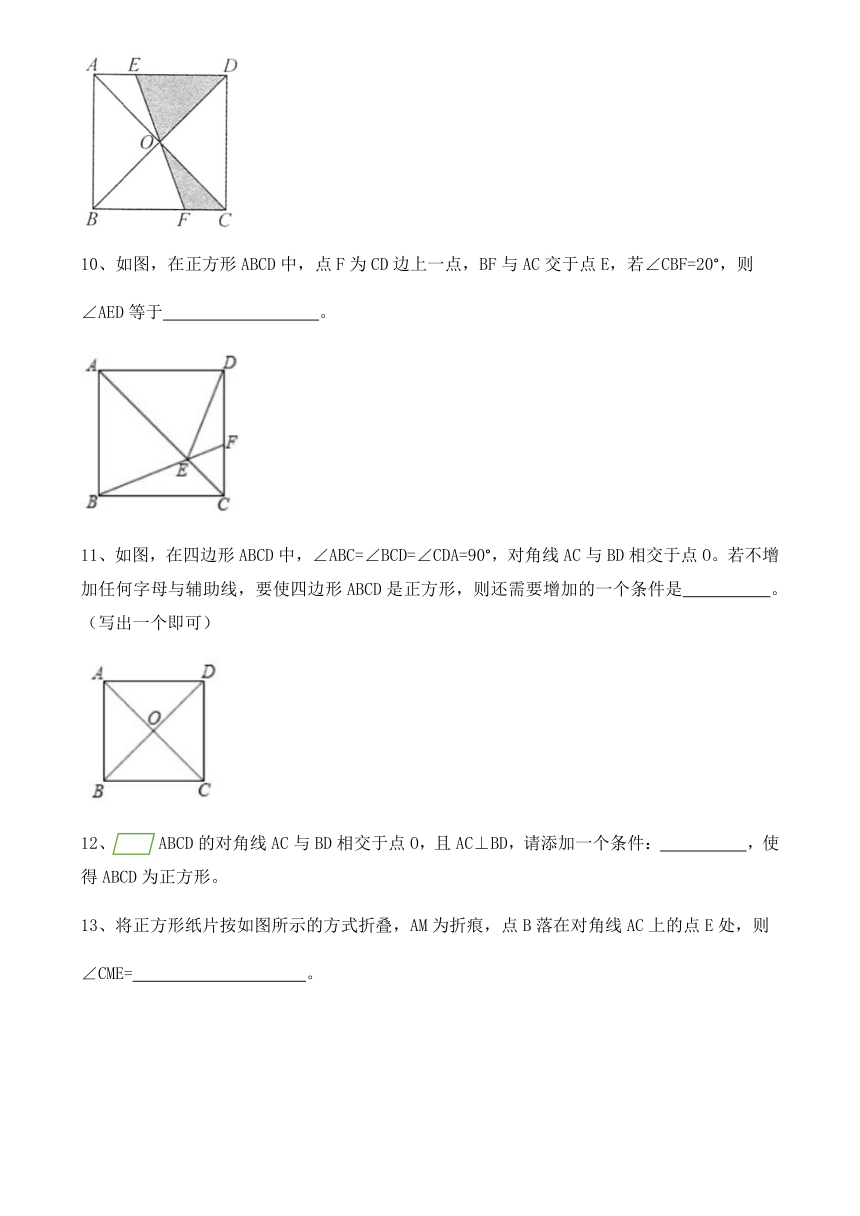
9、如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于E、F,则阴影部分的面积
。
10、如图,在正方形ABCD中,点F为CD边上一点,BF与AC交于点E,若∠CBF=20°,则
∠AED等于
。
11、如图,在四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,对角线AC与BD相交于点O。若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需要增加的一个条件是
。(写出一个即可)
ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:
,使得ABCD为正方形。
将正方形纸片按如图所示的方式折叠,AM为折痕,点B落在对角线AC上的点E处,则
∠CME=
。
解答题
14、如图,菱形ABCD的对角线AC、BD相交于点O,分别延长OA、OC到点E、F,使AE=CF,依次连接B、F、D、E各点。
(1)求证:;
(2)若∠ABC=50°,则当∠EBA=
时,四边形BFDE是正方形。
15、如图①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG、DE。我们探究图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)猜想图①中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图②、③的情形。请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图②证明你的判断。
①
②
③
如图①,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA=EB=FC=GD,连接EG,FH交于点O。
如图②,连接EF、FG、GH、HE,试判断四边形EFGH的形状,并证明你的结论;
将四边形ABCD沿线段EG、HF剪开,再把得到的四个四边形按图③的方式拼接成一个四边形。若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图③中阴影部分的面积为
cm2.
①
②
③
如图,在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE、DE,其中DE交直线AP于点F。
依题意补全图①;
若∠PAB=20°,求∠ADF的度数;
如图②,若45°<∠PAB<90°,用等式表示线段AB、FE、FD之间的数量关系,并证明。
①
②
正方形
一、选择题
1、已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件即可推出该四边形是正方形,那么这个条件可以是(
)
A、∠D=90°
B、AB=CD
C、AD=BC
D、BC=CD
如图,在正方形ABCD中,对角线AC、BD相交于点O,则图中的等腰三角形有(
)
A、4个
B、6个
C、8个
D、10个
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是(
)
BE=AF
B、∠DAF=∠BEC
C、∠AFB+∠BEC=90°
D、AG⊥BE
在四边形ABCD中,O四对角线的交点,能判定这个四边形是正方形的条件是(
)
AC=BD,ABCD
B、AD//BC,∠A=∠C
C、AO=BO=CO=DO,AC⊥BD
D、AO=CO,BO=DO,AB=BC,AB=BC
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE:EC=2:1,则线段CH的长是(
)。
3
B、4
C、5
D、6
在
ABCD中,下列条件不能判断ABCD是正方形的是(
)
∠ABC=90°且AB=AD
B、AB=BC且AC⊥BD
C、AC⊥BD且AC=BD
D、AC=BD
且AB=BC
如图,正方形ABCD的面积是1,则以相邻两边中点连线EF为边的正方形EFGH的周长为(
)
B、2
C、+1
D、2+1
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长度为2,则FM的长为(
)
A、2
B、
C、
D、1
填空题
9、如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于E、F,则阴影部分的面积
。
10、如图,在正方形ABCD中,点F为CD边上一点,BF与AC交于点E,若∠CBF=20°,则
∠AED等于
。
11、如图,在四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,对角线AC与BD相交于点O。若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需要增加的一个条件是
。(写出一个即可)
ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:
,使得ABCD为正方形。
将正方形纸片按如图所示的方式折叠,AM为折痕,点B落在对角线AC上的点E处,则
∠CME=
。
解答题
14、如图,菱形ABCD的对角线AC、BD相交于点O,分别延长OA、OC到点E、F,使AE=CF,依次连接B、F、D、E各点。
(1)求证:;
(2)若∠ABC=50°,则当∠EBA=
时,四边形BFDE是正方形。
15、如图①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG、DE。我们探究图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)猜想图①中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图②、③的情形。请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图②证明你的判断。
①
②
③
如图①,在正方形ABCD中,E、F、G、H分别为边AB、BC、CD、DA上的点,HA=EB=FC=GD,连接EG,FH交于点O。
如图②,连接EF、FG、GH、HE,试判断四边形EFGH的形状,并证明你的结论;
将四边形ABCD沿线段EG、HF剪开,再把得到的四个四边形按图③的方式拼接成一个四边形。若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图③中阴影部分的面积为
cm2.
①
②
③
如图,在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE、DE,其中DE交直线AP于点F。
依题意补全图①;
若∠PAB=20°,求∠ADF的度数;
如图②,若45°<∠PAB<90°,用等式表示线段AB、FE、FD之间的数量关系,并证明。
①
②
