2020--2021学年人教版八年级下册数学18.1平行四边形 强化练习(word解析版)
文档属性
| 名称 | 2020--2021学年人教版八年级下册数学18.1平行四边形 强化练习(word解析版) | 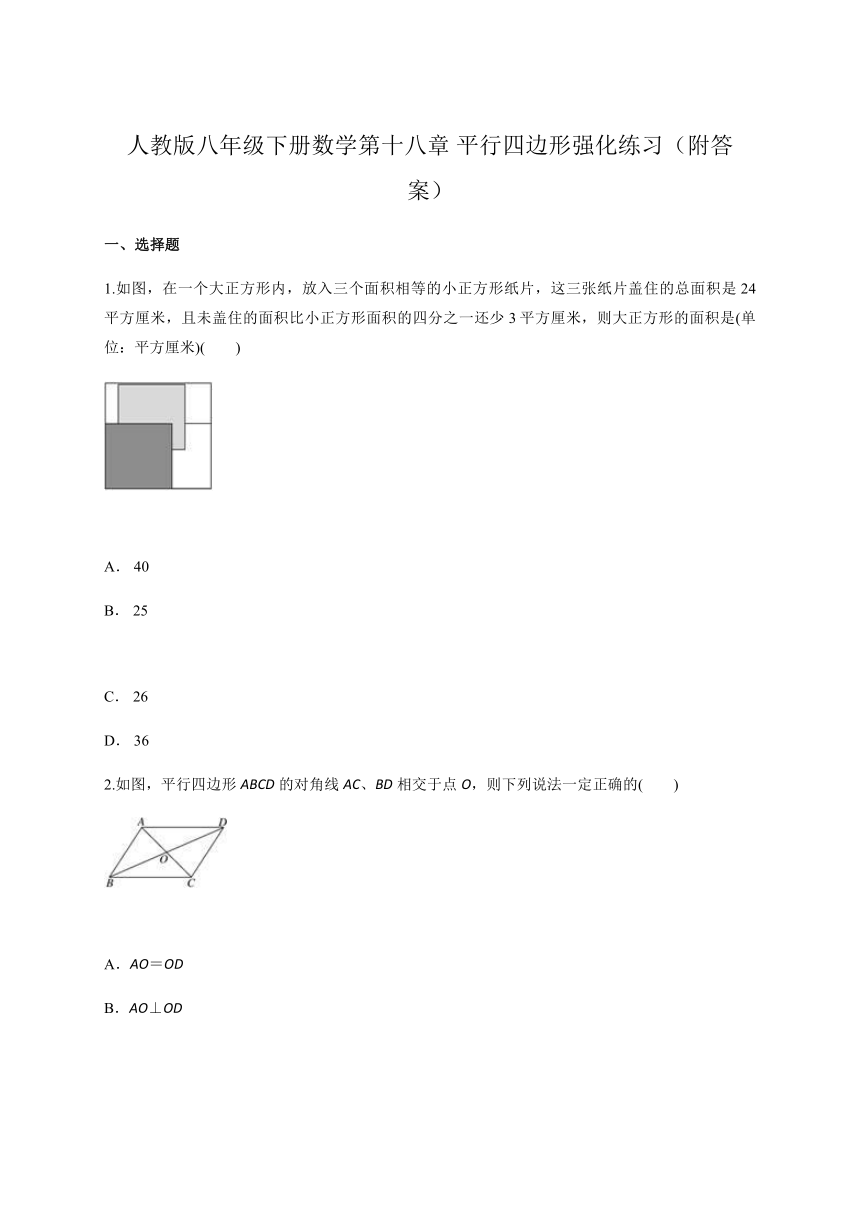 | |
| 格式 | docx | ||
| 文件大小 | 46.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 17:55:06 | ||
图片预览





文档简介
人教版八年级下册数学第十八章
平行四边形强化练习(附答案)
一、选择题
1.如图,在一个大正方形内,放入三个面积相等的小正方形纸片,这三张纸片盖住的总面积是24平方厘米,且未盖住的面积比小正方形面积的四分之一还少3平方厘米,则大正方形的面积是(单位:平方厘米)( )
A.
40
B.
25
C.
26
D.
36
2.如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB
3.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
A.
100°
B.
110°
C.
120°
D.
125°
4.下列说法中错误的是( )
A.
平行四边形的对角线互相平分
B.
两组对边分别相等的四边形是平行四边形
C.
矩形的对角线相等
D.
有一组邻边相等且有一个角是直角的四边形是正方形
5.如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是( )
①图甲,DE⊥AC,BF⊥AC
②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点
④图丁,E是AB上一点,EF⊥AB.
A.
3
B.
4
C.
1
D.
2
6.如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形有( )
A.
1对
B.
2对
C.
3对
D.
4对
7.如图,矩形ABCD的对角线交于点O,若∠ACB=30°,AB=2,则OC的长为( )
A.
2
B.
3
C.
2
D.
4
二、填空题
8.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足____________(关系)时,四边形EFGH为矩形.
9.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为__________.
10.?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:__________,使得?ABCD为正方形.
11.如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是__________(只需填写正确结论的序号).
12.在?ABCD中,两对角线交于点O,点E,F,G,H分别是AO,BO,CO,DO的中点,那么以图中的点为顶点的平行四边形共有__________个.
三、解答题
13.如图,在矩形ABCD中,AB=24
cm,BC=8
cm,点P从A开始沿折线A-B-C-D以4
cm/s的速度移动,点Q从C开始沿CD边以2
cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
14.如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC满足什么条件时,四边形ADFE是矩形;
(2)当∠BAC满足什么条件时,平行四边形ADFE不存在;
(3)当△ABC分别满足什么条件时,平行四边形ADFE是菱形,正方形?
15.已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,且AO=CO.求证:四边形ABCD是平行四边形.
答案解析
1.【答案】B
【解析】设小正方形的边长为a,大正方形的边长为b,
由这三张纸片盖住的总面积是24平方厘米,可得ab+a(b-a)=24,①
由未盖住的面积比小正方形面积的四分之一还少3平方厘米,可得(b-a)2=a2-3,②
将①②联立解方程组可得:a=4,b=5,
∴大正方形的边长为5,
∴面积是25.
故选B.
2.【答案】C
【解析】∵四边形ABCD是平行四边形,
∴OA=OC;
故选C.
3.【答案】C
【解析】∵AD=CB,AB=CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AD∥BC,
∴∠A+∠ABC=180°,
∵∠ABC+∠ADC=120°,
∴∠ABC=60°,
∴∠A=120°,
故选C.
4.【答案】D
【解析】A.对角线互相平分是平行四边形的一条重要性质,故该选项正确;
B.两组对边分别相等的四边形是平行四边形,这是平行四边形的定义,故该选项正确;
C.矩形的对角线相等,是矩形的重要性质,故该选项正确;
D.有一组邻边相等且有一个角是直角的平行四边形是正方形,而不是一般的四边形,故该选项错误.
故选D.
5.【答案】A
【解析】①∵四边形ABCD是平行四边形,
∴S△ACD=S△ABC,
∵DE⊥AC,BF⊥AC,
∴DE∥BF,S△ACD=AC·DE,S△ABC=AC·BF,
∴DE=BF,
∴四边形BFDE是平行四边形;
②∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=CB,AD∥BC,
∴∠DAE=∠BCF,
∵DE平分∠ADC,BF平分∠ABC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形BFDE是平行四边形;
③∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB的中点,F是CD的中点,
∴DF=CD,BE=AB,
∴DF=BE,
∴四边形BFDE是平行四边形;
④∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB上一点,EF⊥AB,
无法判定DF=BE,
∴四边形BFDE不一定是平行四边形.
故选A.
6.【答案】D
【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中,
∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.
7.【答案】A
【解析】在矩形ABCD中,∠ABC=90°,
∵∠ACB=30°,AB=2,
∴AC=2AB=2×2=4,
∵四边形ABCD是矩形,
∴OC=OA=AC=2.
故选A.
8.【答案】AD=AB
【解析】∵四边形ABCD是矩形,
∴∠A=90°.
∵AE=AF,
∴∠AFE=∠AEF=45°.
又∵EH⊥EF,FG⊥EF,
∴∠GFB=∠HED=45°,
∴△DHE和△BGF都是等腰直角三角形.
如果四边形EFGH是矩形,则EH=FG,
∴ED=FB,
又∵AE=AF,
∴AD=AB.
9.【答案】(0,)
【解析】过D作DE⊥AC于E,
∵四边形ABCO是矩形,B(4,3),
∴OC=AB=3,OA=BC=4,∠COA=90°,
∵AD平分∠OAC,
∴OD=DE,
由勾股定理得OA2=AD2-OD2,AE2=AD2-DE2,
∴OA=AE=4,
由勾股定理得AC==5,
在Rt△DEC中,DE2+EC2=CD2,
即OD2+(5-4)2=(3-OD)2,
解得OD=,
所以D的坐标为(0,),
10.【答案】∠BAD=90°
【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,
∴?ABCD是菱形,
当∠BAD=90°时,?ABCD为正方形.
11.【答案】①③④
【解析】①∵△AEF是等边三角形,
∴∠EAF=60°,AE=AF,
又∵AE⊥BC,AF⊥CD,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥CD,∠C=∠BAD=120°,
∴∠B=180°-∠C=60°,故①正确;
②∵∠D=∠B=60°,
∴∠BAE=∠DAF=90°-60°=30°,
∴∠EAF=120°-30°-30°=60°,
但是AE不一定等于AF,故②错误;
③若AE=AF,则BC·AE=CD·AF,
∴BC=CD,
∴平行四边形ABCD是菱形,故③正确;
④若平行四边形ABCD是菱形,
则BC=CD,
∴BC·AE=CD·AF,
∴AE=AF,故④正确;
故答案为①③④.
12.【答案】4
【解析】根据对角线互相平分的四边形是平行四边形,可判定四边形EFGH是平行四边形;根据SAS可分别证明:△AHD≌△CFB,△AFB≌△CHD,可得AH=CF,AF=CH,所以AHCF是平行四边形;同理可得BGDE是平行四边形,则以图中的点为顶点的平行四边形是四边形EFGH、ABCD、AHCF、BGDE,故有4个.
13.【答案】解 根据题意得:CQ=2t,AP=4t,
则BP=24-4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24-4t,
解得t=4,
答:当t=4
s时,四边形QPBC是矩形.
【解析】求出CQ=2t,AP=4t,BP=24-4t,由已知推出∠B=∠C=90°,CD∥AB,推出CQ=BP时,四边形QPBC是矩形,得出方程2t=24-4t,求出即可.
14.【答案】解 (1)当∠BAC=150°时,四边形ADFE是矩形,
∴∠DAE=360°-120°-150°=90°;
∵四边形ADFE是平行四边形,
∴四边形ADFE是矩形(有一个角是直角的平行四边形是矩形);
(2)当∠BAC=60°时,平行四边形ADFE不存在,
∠DAE=180°-60°-60°-60°=0°;
(3)当AB=AC且∠BAC不等于60°时,平行四边形ADFE是菱形.
当AB=AC,∠BAC=150°时,平行四边形ADFE是正方形.
【解析】(1)根据矩形的四角相等为90度求解;
(2)根据D、A、E在同一条直线上时不能构成四边形求解;
(3)分别根据菱形的四边相等和正方形的四边相等,四角相等的特性解题.
15.【答案】证明 ∵AB∥CD,
∴∠BAO=∠DCO,
在△AOB和△COD中,
∴△AOB≌△COD(ASA),
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形.
【解析】由AB∥CD,AO=CO,利用ASA,可判定△AOB≌△COD,则可证得AB=CD,然后由一组对边平行且相等的四边形是平行四边形,证得四边形ABCD是平行四边形.
平行四边形强化练习(附答案)
一、选择题
1.如图,在一个大正方形内,放入三个面积相等的小正方形纸片,这三张纸片盖住的总面积是24平方厘米,且未盖住的面积比小正方形面积的四分之一还少3平方厘米,则大正方形的面积是(单位:平方厘米)( )
A.
40
B.
25
C.
26
D.
36
2.如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB
3.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
A.
100°
B.
110°
C.
120°
D.
125°
4.下列说法中错误的是( )
A.
平行四边形的对角线互相平分
B.
两组对边分别相等的四边形是平行四边形
C.
矩形的对角线相等
D.
有一组邻边相等且有一个角是直角的四边形是正方形
5.如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是( )
①图甲,DE⊥AC,BF⊥AC
②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点
④图丁,E是AB上一点,EF⊥AB.
A.
3
B.
4
C.
1
D.
2
6.如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形有( )
A.
1对
B.
2对
C.
3对
D.
4对
7.如图,矩形ABCD的对角线交于点O,若∠ACB=30°,AB=2,则OC的长为( )
A.
2
B.
3
C.
2
D.
4
二、填空题
8.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足____________(关系)时,四边形EFGH为矩形.
9.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为__________.
10.?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:__________,使得?ABCD为正方形.
11.如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是__________(只需填写正确结论的序号).
12.在?ABCD中,两对角线交于点O,点E,F,G,H分别是AO,BO,CO,DO的中点,那么以图中的点为顶点的平行四边形共有__________个.
三、解答题
13.如图,在矩形ABCD中,AB=24
cm,BC=8
cm,点P从A开始沿折线A-B-C-D以4
cm/s的速度移动,点Q从C开始沿CD边以2
cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
14.如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC满足什么条件时,四边形ADFE是矩形;
(2)当∠BAC满足什么条件时,平行四边形ADFE不存在;
(3)当△ABC分别满足什么条件时,平行四边形ADFE是菱形,正方形?
15.已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,且AO=CO.求证:四边形ABCD是平行四边形.
答案解析
1.【答案】B
【解析】设小正方形的边长为a,大正方形的边长为b,
由这三张纸片盖住的总面积是24平方厘米,可得ab+a(b-a)=24,①
由未盖住的面积比小正方形面积的四分之一还少3平方厘米,可得(b-a)2=a2-3,②
将①②联立解方程组可得:a=4,b=5,
∴大正方形的边长为5,
∴面积是25.
故选B.
2.【答案】C
【解析】∵四边形ABCD是平行四边形,
∴OA=OC;
故选C.
3.【答案】C
【解析】∵AD=CB,AB=CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AD∥BC,
∴∠A+∠ABC=180°,
∵∠ABC+∠ADC=120°,
∴∠ABC=60°,
∴∠A=120°,
故选C.
4.【答案】D
【解析】A.对角线互相平分是平行四边形的一条重要性质,故该选项正确;
B.两组对边分别相等的四边形是平行四边形,这是平行四边形的定义,故该选项正确;
C.矩形的对角线相等,是矩形的重要性质,故该选项正确;
D.有一组邻边相等且有一个角是直角的平行四边形是正方形,而不是一般的四边形,故该选项错误.
故选D.
5.【答案】A
【解析】①∵四边形ABCD是平行四边形,
∴S△ACD=S△ABC,
∵DE⊥AC,BF⊥AC,
∴DE∥BF,S△ACD=AC·DE,S△ABC=AC·BF,
∴DE=BF,
∴四边形BFDE是平行四边形;
②∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=CB,AD∥BC,
∴∠DAE=∠BCF,
∵DE平分∠ADC,BF平分∠ABC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形BFDE是平行四边形;
③∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB的中点,F是CD的中点,
∴DF=CD,BE=AB,
∴DF=BE,
∴四边形BFDE是平行四边形;
④∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB上一点,EF⊥AB,
无法判定DF=BE,
∴四边形BFDE不一定是平行四边形.
故选A.
6.【答案】D
【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中,
∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.
7.【答案】A
【解析】在矩形ABCD中,∠ABC=90°,
∵∠ACB=30°,AB=2,
∴AC=2AB=2×2=4,
∵四边形ABCD是矩形,
∴OC=OA=AC=2.
故选A.
8.【答案】AD=AB
【解析】∵四边形ABCD是矩形,
∴∠A=90°.
∵AE=AF,
∴∠AFE=∠AEF=45°.
又∵EH⊥EF,FG⊥EF,
∴∠GFB=∠HED=45°,
∴△DHE和△BGF都是等腰直角三角形.
如果四边形EFGH是矩形,则EH=FG,
∴ED=FB,
又∵AE=AF,
∴AD=AB.
9.【答案】(0,)
【解析】过D作DE⊥AC于E,
∵四边形ABCO是矩形,B(4,3),
∴OC=AB=3,OA=BC=4,∠COA=90°,
∵AD平分∠OAC,
∴OD=DE,
由勾股定理得OA2=AD2-OD2,AE2=AD2-DE2,
∴OA=AE=4,
由勾股定理得AC==5,
在Rt△DEC中,DE2+EC2=CD2,
即OD2+(5-4)2=(3-OD)2,
解得OD=,
所以D的坐标为(0,),
10.【答案】∠BAD=90°
【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,
∴?ABCD是菱形,
当∠BAD=90°时,?ABCD为正方形.
11.【答案】①③④
【解析】①∵△AEF是等边三角形,
∴∠EAF=60°,AE=AF,
又∵AE⊥BC,AF⊥CD,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥CD,∠C=∠BAD=120°,
∴∠B=180°-∠C=60°,故①正确;
②∵∠D=∠B=60°,
∴∠BAE=∠DAF=90°-60°=30°,
∴∠EAF=120°-30°-30°=60°,
但是AE不一定等于AF,故②错误;
③若AE=AF,则BC·AE=CD·AF,
∴BC=CD,
∴平行四边形ABCD是菱形,故③正确;
④若平行四边形ABCD是菱形,
则BC=CD,
∴BC·AE=CD·AF,
∴AE=AF,故④正确;
故答案为①③④.
12.【答案】4
【解析】根据对角线互相平分的四边形是平行四边形,可判定四边形EFGH是平行四边形;根据SAS可分别证明:△AHD≌△CFB,△AFB≌△CHD,可得AH=CF,AF=CH,所以AHCF是平行四边形;同理可得BGDE是平行四边形,则以图中的点为顶点的平行四边形是四边形EFGH、ABCD、AHCF、BGDE,故有4个.
13.【答案】解 根据题意得:CQ=2t,AP=4t,
则BP=24-4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24-4t,
解得t=4,
答:当t=4
s时,四边形QPBC是矩形.
【解析】求出CQ=2t,AP=4t,BP=24-4t,由已知推出∠B=∠C=90°,CD∥AB,推出CQ=BP时,四边形QPBC是矩形,得出方程2t=24-4t,求出即可.
14.【答案】解 (1)当∠BAC=150°时,四边形ADFE是矩形,
∴∠DAE=360°-120°-150°=90°;
∵四边形ADFE是平行四边形,
∴四边形ADFE是矩形(有一个角是直角的平行四边形是矩形);
(2)当∠BAC=60°时,平行四边形ADFE不存在,
∠DAE=180°-60°-60°-60°=0°;
(3)当AB=AC且∠BAC不等于60°时,平行四边形ADFE是菱形.
当AB=AC,∠BAC=150°时,平行四边形ADFE是正方形.
【解析】(1)根据矩形的四角相等为90度求解;
(2)根据D、A、E在同一条直线上时不能构成四边形求解;
(3)分别根据菱形的四边相等和正方形的四边相等,四角相等的特性解题.
15.【答案】证明 ∵AB∥CD,
∴∠BAO=∠DCO,
在△AOB和△COD中,
∴△AOB≌△COD(ASA),
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形.
【解析】由AB∥CD,AO=CO,利用ASA,可判定△AOB≌△COD,则可证得AB=CD,然后由一组对边平行且相等的四边形是平行四边形,证得四边形ABCD是平行四边形.
