2020-2021学年人教版七年级下册数学5.3.1平行线的性质 同步练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版七年级下册数学5.3.1平行线的性质 同步练习(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 20:04:13 | ||
图片预览
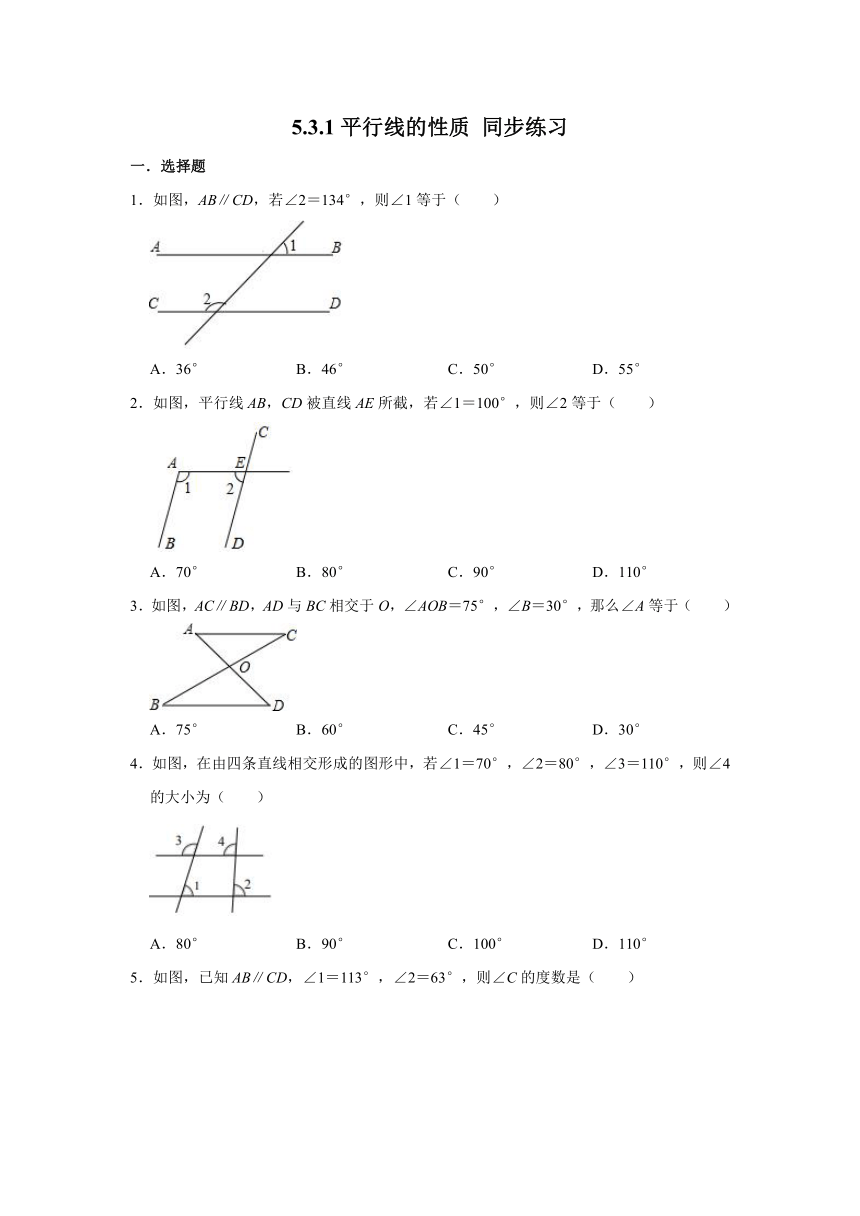



文档简介
5.3.1平行线的性质 同步练习
一.选择题
1.如图,AB∥CD,若∠2=134°,则∠1等于( )
A.36° B.46° C.50° D.55°
2.如图,平行线AB,CD被直线AE所截,若∠1=100°,则∠2等于( )
A.70° B.80° C.90° D.110°
3.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75° B.60° C.45° D.30°
4.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80° B.90° C.100° D.110°
5.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40° B.45° C.50° D.60°
6.如图,AB∥CD,CA平分∠DCB,且∠B=110°,则∠A的度数为( )
A.35° B.45° C.55° D.70°
7.如图,直线AB∥DE,AB与DF相交于点C,CE⊥DF,∠FCB=33°,则∠E的度数是( )
A.33° B.47° C.53° D.57°
8.下列图形中,由AB∥CD能得到∠1=∠2的是( )
A.
B.
C.
D.
9.下列四个图形中,不能推出∠2与∠1相等的是( )
A. B.
C. D.
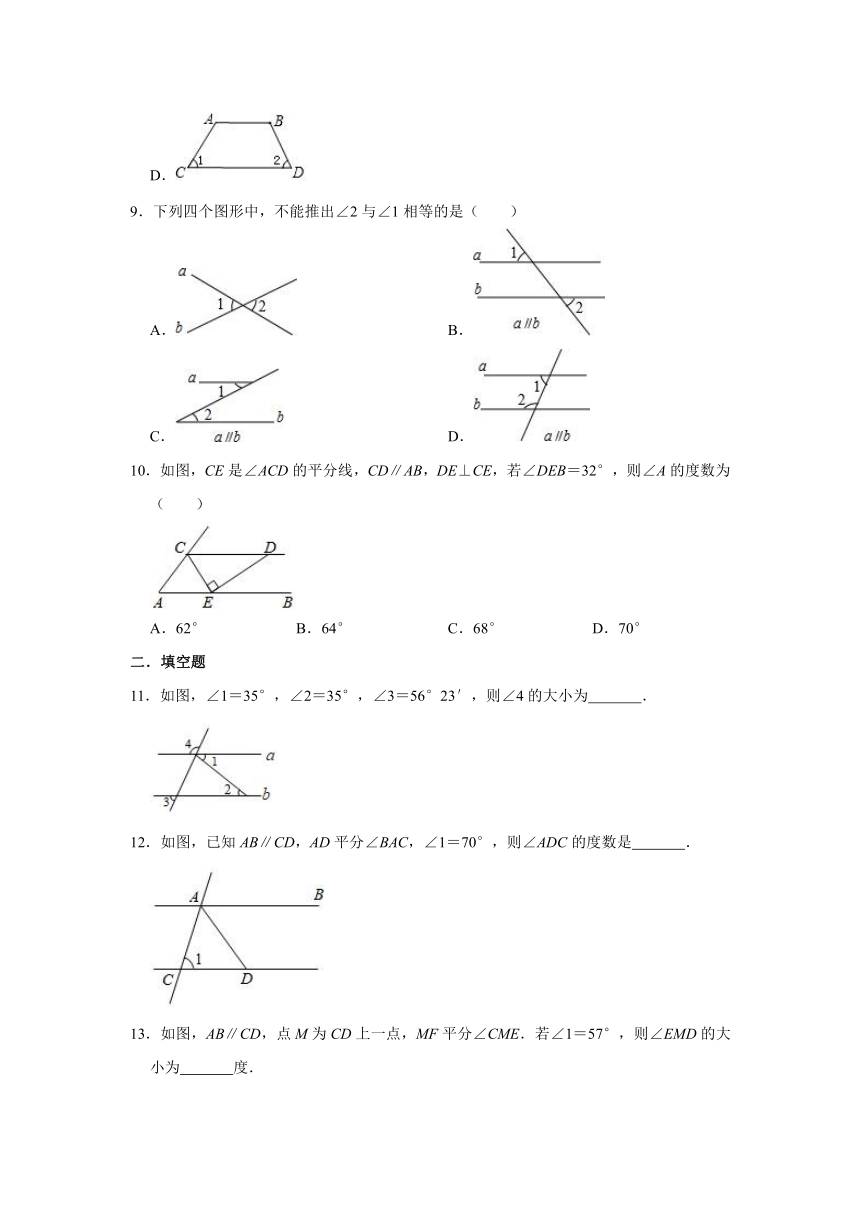
10.如图,CE是∠ACD的平分线,CD∥AB,DE⊥CE,若∠DEB=32°,则∠A的度数为( )
A.62° B.64° C.68° D.70°
二.填空题
11.如图,∠1=35°,∠2=35°,∠3=56°23′,则∠4的大小为 .
12.如图,已知AB∥CD,AD平分∠BAC,∠1=70°,则∠ADC的度数是 .
13.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
14.如图,a∥b,直角三角板直角顶点在直线b上.已知∠1=50°,则∠2的度数为 度.
15.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
三.解答题
16.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O= =40°( )
又∵OB∥DE(已知)
∴ =∠1= °( )
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ= °.
17.如图,直线AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,求∠AED的度数.
18.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,求∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
参考答案
一.选择题
1.解:∵AB∥CD,
∴∠2=∠3,
∵∠2=134°,
∴∠3=134°,
∵∠3+∠1=180°,
∴∠1=46°,
故选:B.
2.解:∵AB∥CD,
∴∠1+∠2=180°.
又∵∠1=100°,
∴∠2=180°﹣100°=80°.
故选:B.
3.解:∵∠AOB=75°,∠B=30°,
∴∠D=∠AOB﹣∠B=45°,
∵AC∥BD,
∴∠A=∠D=45°,
故选:C.
4.解:如图,
∵∠1=70°,
∴∠5=180°﹣70°=110°,
∴∠5=∠3=110°,
∴a∥b,
∴∠2+∠6=180°,
∵∠2=80°,
∴∠6=100°,
∴∠4=∠6=100°.
故选:C.
5.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
6.解:∵AB∥CD,
∴∠DCB+∠B=180°,
∵∠B=110°,
∴∠DCB=180°﹣∠B=180°﹣110°=70°,
∵CA平分∠DCB,
∴∠ACD=∠DCB=35°,
∵AB∥CD,
∴∠A=∠ACD=35°.
故选:A.
7.解:∵AB∥DE,∠FCB=33°,
∴∠D=∠FCB=33°,
又∵CE⊥DF,
∴∠DCE=90°,
∴∠D+∠E=90°,
则∠E=90°﹣∠D=57°,
故选:D.
8.解:A、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,故A正确;
B、∵AB∥CD,
∴∠1+∠2=180°,故A错误;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,故D错误.
故选:A.
9.解:A、∵∠1和∠2互为对顶角,
∴∠1=∠2,故本选项不合题意;
B、如图,∵a∥b,
∴∠1=∠3(两直线平行,同位角相等),
∵∠2=∠3(对顶角相等),
∴∠1=∠2,故本选项不合题意;
C、∵a∥b,
∴∠1=∠2(两直线平行,内错角相等),故本选项不合题意;
D、∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
不能判断∠1=∠2,故本选项符合题意;
故选:D.
10.解:∵CE是∠ACD的平分线,
∴∠ACE=∠DCE,
∵DE⊥CE,
∴∠CDE+∠DCE=90°,∠BED+∠AEC=90°,
∵∠DEB=32°,
∴∠AEC=90°﹣∠DEB=90°﹣32°=58°,
∵CD∥AB,
∴∠CDE=∠BED,
∴∠DCE=∠AEC,
∴∠ACE=∠AEC,
∴∠A=180°﹣2∠AEC=180°﹣2×58°=64°.
故选:B.
二.填空题
11.解:如图,
∵∠1=35°,∠2=35°,
∴∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠3=56°23′,
∴∠5=180°﹣∠3=123°37′,
∴∠4=123°37′.
故答案为:123°37′.
12.解:∵AB∥CD,
∴∠1+∠BAC=180°,
∴∠BAC=180°﹣∠1=180°﹣70°=110°.
∵AD平分∠BAC,
∴∠BAD=∠BAC=×110°=55°.
∵AB∥CD,
∴∠ADC=∠BAD=55°.
故答案为:55°.
13.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
14.解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1=90°﹣50°=40°,
∵a∥b,
∴∠2=∠3=40°,
故答案为:40.
15.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
三.解答题
16.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
17.解:∵AB∥CD,
∴∠BAE+∠AED=180°,∠BAC+∠C=180°,
∵∠C=50°,
∴∠BAC=130°,
∵AE平分∠BAC,
∴∠BAE=BAC=65°,
∴∠AED=180°﹣∠BAE=115°.
18.(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
一.选择题
1.如图,AB∥CD,若∠2=134°,则∠1等于( )
A.36° B.46° C.50° D.55°
2.如图,平行线AB,CD被直线AE所截,若∠1=100°,则∠2等于( )
A.70° B.80° C.90° D.110°
3.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75° B.60° C.45° D.30°
4.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80° B.90° C.100° D.110°
5.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40° B.45° C.50° D.60°
6.如图,AB∥CD,CA平分∠DCB,且∠B=110°,则∠A的度数为( )
A.35° B.45° C.55° D.70°
7.如图,直线AB∥DE,AB与DF相交于点C,CE⊥DF,∠FCB=33°,则∠E的度数是( )
A.33° B.47° C.53° D.57°
8.下列图形中,由AB∥CD能得到∠1=∠2的是( )
A.
B.
C.
D.
9.下列四个图形中,不能推出∠2与∠1相等的是( )
A. B.
C. D.
10.如图,CE是∠ACD的平分线,CD∥AB,DE⊥CE,若∠DEB=32°,则∠A的度数为( )
A.62° B.64° C.68° D.70°
二.填空题
11.如图,∠1=35°,∠2=35°,∠3=56°23′,则∠4的大小为 .
12.如图,已知AB∥CD,AD平分∠BAC,∠1=70°,则∠ADC的度数是 .
13.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
14.如图,a∥b,直角三角板直角顶点在直线b上.已知∠1=50°,则∠2的度数为 度.
15.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
三.解答题
16.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O= =40°( )
又∵OB∥DE(已知)
∴ =∠1= °( )
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ= °.
17.如图,直线AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,求∠AED的度数.
18.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,求∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
参考答案
一.选择题
1.解:∵AB∥CD,
∴∠2=∠3,
∵∠2=134°,
∴∠3=134°,
∵∠3+∠1=180°,
∴∠1=46°,
故选:B.
2.解:∵AB∥CD,
∴∠1+∠2=180°.
又∵∠1=100°,
∴∠2=180°﹣100°=80°.
故选:B.
3.解:∵∠AOB=75°,∠B=30°,
∴∠D=∠AOB﹣∠B=45°,
∵AC∥BD,
∴∠A=∠D=45°,
故选:C.
4.解:如图,
∵∠1=70°,
∴∠5=180°﹣70°=110°,
∴∠5=∠3=110°,
∴a∥b,
∴∠2+∠6=180°,
∵∠2=80°,
∴∠6=100°,
∴∠4=∠6=100°.
故选:C.
5.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
6.解:∵AB∥CD,
∴∠DCB+∠B=180°,
∵∠B=110°,
∴∠DCB=180°﹣∠B=180°﹣110°=70°,
∵CA平分∠DCB,
∴∠ACD=∠DCB=35°,
∵AB∥CD,
∴∠A=∠ACD=35°.
故选:A.
7.解:∵AB∥DE,∠FCB=33°,
∴∠D=∠FCB=33°,
又∵CE⊥DF,
∴∠DCE=90°,
∴∠D+∠E=90°,
则∠E=90°﹣∠D=57°,
故选:D.
8.解:A、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,故A正确;
B、∵AB∥CD,
∴∠1+∠2=180°,故A错误;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,故D错误.
故选:A.
9.解:A、∵∠1和∠2互为对顶角,
∴∠1=∠2,故本选项不合题意;
B、如图,∵a∥b,
∴∠1=∠3(两直线平行,同位角相等),
∵∠2=∠3(对顶角相等),
∴∠1=∠2,故本选项不合题意;
C、∵a∥b,
∴∠1=∠2(两直线平行,内错角相等),故本选项不合题意;
D、∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补),
不能判断∠1=∠2,故本选项符合题意;
故选:D.
10.解:∵CE是∠ACD的平分线,
∴∠ACE=∠DCE,
∵DE⊥CE,
∴∠CDE+∠DCE=90°,∠BED+∠AEC=90°,
∵∠DEB=32°,
∴∠AEC=90°﹣∠DEB=90°﹣32°=58°,
∵CD∥AB,
∴∠CDE=∠BED,
∴∠DCE=∠AEC,
∴∠ACE=∠AEC,
∴∠A=180°﹣2∠AEC=180°﹣2×58°=64°.
故选:B.
二.填空题
11.解:如图,
∵∠1=35°,∠2=35°,
∴∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠3=56°23′,
∴∠5=180°﹣∠3=123°37′,
∴∠4=123°37′.
故答案为:123°37′.
12.解:∵AB∥CD,
∴∠1+∠BAC=180°,
∴∠BAC=180°﹣∠1=180°﹣70°=110°.
∵AD平分∠BAC,
∴∠BAD=∠BAC=×110°=55°.
∵AB∥CD,
∴∠ADC=∠BAD=55°.
故答案为:55°.
13.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
14.解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1=90°﹣50°=40°,
∵a∥b,
∴∠2=∠3=40°,
故答案为:40.
15.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
三.解答题
16.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
17.解:∵AB∥CD,
∴∠BAE+∠AED=180°,∠BAC+∠C=180°,
∵∠C=50°,
∴∠BAC=130°,
∵AE平分∠BAC,
∴∠BAE=BAC=65°,
∴∠AED=180°﹣∠BAE=115°.
18.(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
