安徽省六安市金寨县2020-2021学年九年级上学期期末检测数学试题(Word版 含答案)
文档属性
| 名称 | 安徽省六安市金寨县2020-2021学年九年级上学期期末检测数学试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 20:11:16 | ||
图片预览

文档简介
金寨县
2020~2021
学年度第一学期九年级数学期末质量监测试卷
考生注意;
本试卷共
150
分,考试时间
120
分钟.
2.
请将各题答案填在答题卡上.
一、选择题(本大题共
10
小题,每小题4分,满分
40
分)
1.下对度形中,既是轴对称图形,又是中心对称图形的是
2如图,PA
是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠BAP=116°则∠P的度
数为
A.64°
B.26°
52°
D.38°
3.共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,若第二个月的增长率是x,第三个月的增长率是第二个月的两倍,那么y与x的函数关系是
A.
y=a(1+x)(1+2x)
B.
y=a(1+x)2
C.
y=2a(1+x)2
D.
y=2x2+a
4已知点A(x,y)在反比例函数的图象上,若x>2,则y的取值范围是
A.3B
y<3
C.
0D.
y>3
5.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与
AD
相交于点F.则图中与△ABD相似的是
A.△ABC
B.
△ABF
C.△BFD
D.
△AEF
6.如图,AB是⊙O的直径,C,D是上的三等分点,且sin∠ABC=,则∠A+∠D
等于
A.120°
B.95°
C.105°
D.150°
7.如图,AB是⊙O的直径,CD是弦,四边形OBCD是菱形,AC与OD
相交于点P,则下列结论错误的是
A.
OD⊥AC
B.AC平分OD
C
.CB=2DP
D.
AP=2OP
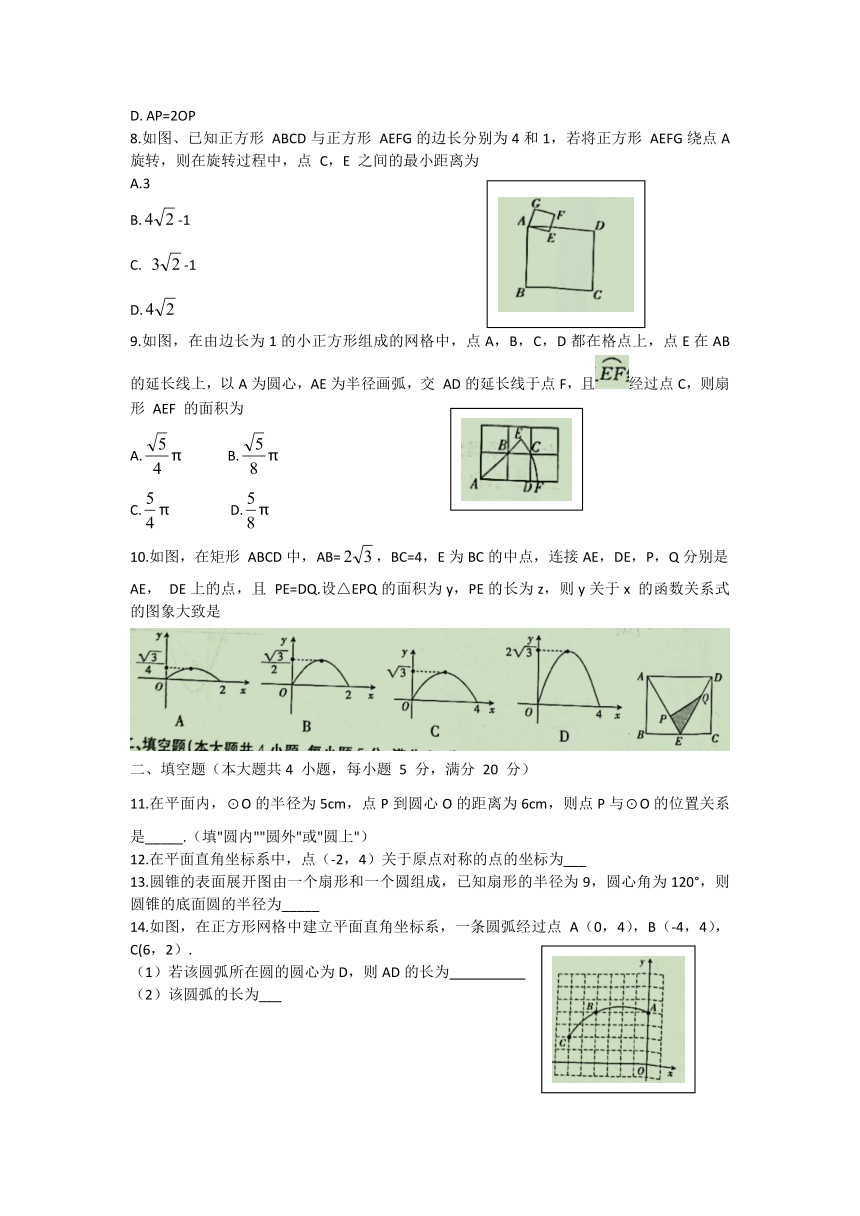
8.如图、已知正方形
ABCD与正方形
AEFG的边长分别为4和1,若将正方形
AEFG绕点A旋转,则在旋转过程中,点
C,E
之间的最小距离为
A.3
B.-1
C.
-1
D.
9.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点上,点E在AB的延长线上,以A为圆心,AE为半径画弧,交
AD的延长线于点F,且经过点C,则扇形
AEF
的面积为
A.π
B.π
C.π
D.π
10.如图,在矩形
ABCD中,AB=,BC=4,E为BC的中点,连接AE,DE,P,Q分别是AE,
DE上的点,且
PE=DQ.设△EPQ的面积为y,PE的长为z,则y关于x
的函数关系式的图象大致是
二、填空题(本大题共4
小题,每小题
5
分,满分
20
分)
11.在平面内,⊙O的半径为5cm,点P到圆心O的距离为6cm,则点P与⊙O的位置关系是_____.(填"圆内""圆外"或"圆上")
12.在平面直角坐标系中,点(-2,4)关于原点对称的点的坐标为___
13.圆锥的表面展开图由一个扇形和一个圆组成,已知扇形的半径为9,圆心角为120°,则圆锥的底面圆的半径为_____
14.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过点
A(0,4),B(-4,4),C(6,2).
(1)若该圆弧所在圆的圆心为D,则AD的长为
(2)该圆弧的长为___
三、(本大题共
2
小题,每小题
8
分,满分
16
分)
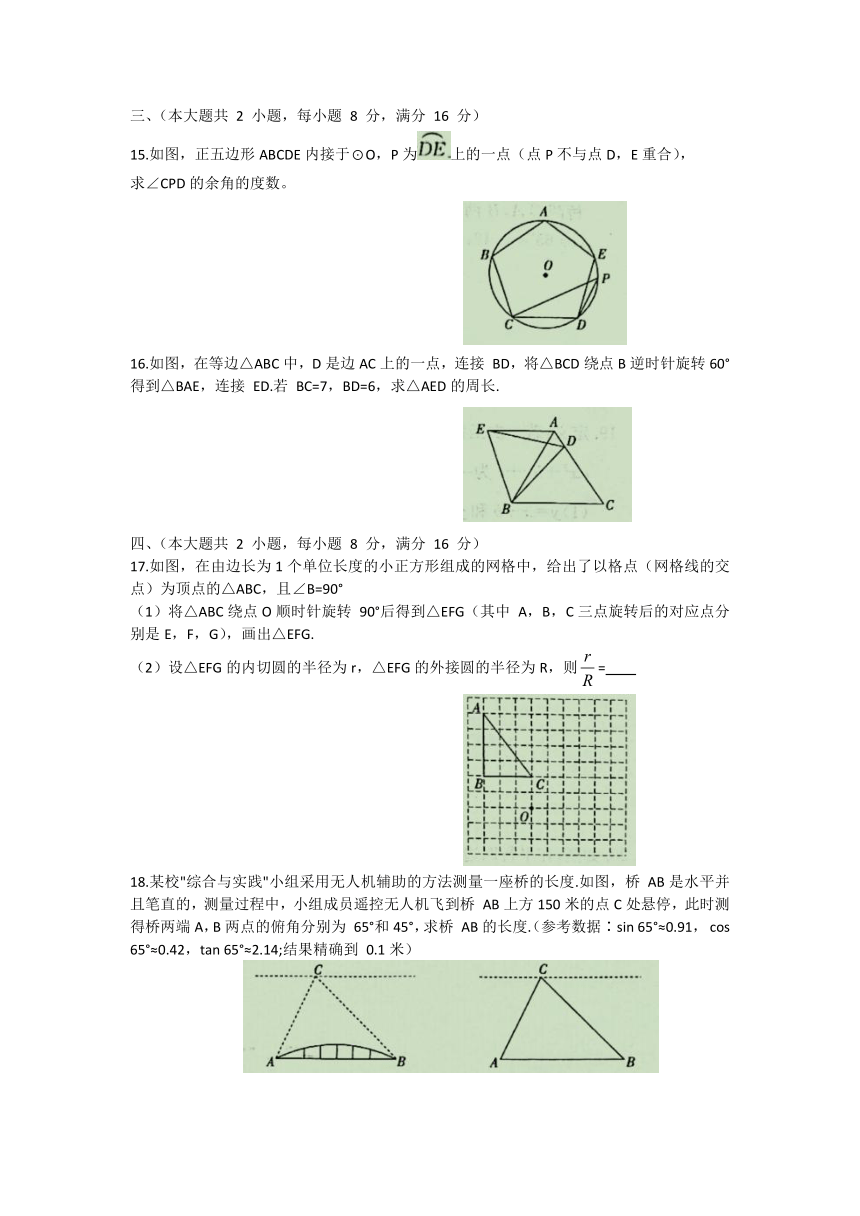
15.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D,E重合),
求∠CPD的余角的度数。
16.如图,在等边△ABC中,D是边AC上的一点,连接
BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接
ED.若
BC=7,BD=6,求△AED的周长.
四、(本大题共
2
小题,每小题
8
分,满分
16
分)
17.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的△ABC,且∠B=90°
(1)将△ABC绕点O顺时针旋转
90°后得到△EFG(其中
A,B,C三点旋转后的对应点分别是E,F,G),画出△EFG.
(2)设△EFG的内切圆的半径为r,△EFG的外接圆的半径为R,则=
18.某校"综合与实践"小组采用无人机辅助的方法测量一座桥的长度.如图,桥
AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥
AB上方150米的点C处悬停,此时测得桥两端A,B两点的俯角分别为
65°和45°,求桥
AB的长度.(参考数据∶sin
65°≈0.91,
cos
65°≈0.42,tan
65°≈2.14;结果精确到
0.1米)
五、(本大题共
2
小题,每小题
10
分,满分
20
分)
19.定义∶若一次函数
y=ax+b(a≠0)和反比例函数y=-(c≠0)满足a-b=b-c,则
y=ax?+bx+c
为一次函数和反比例函数的"等差"函数.
(1)y=x+b和y=-是否存在"等差"函数?若存在,请写出它们的"等差"函数.
(2)若y=5x+b和y=-存在"等差"函数,且"等差"函数的图象与y=-的图象的一个交点的横坐标为
1,求反比例函数的表达式.
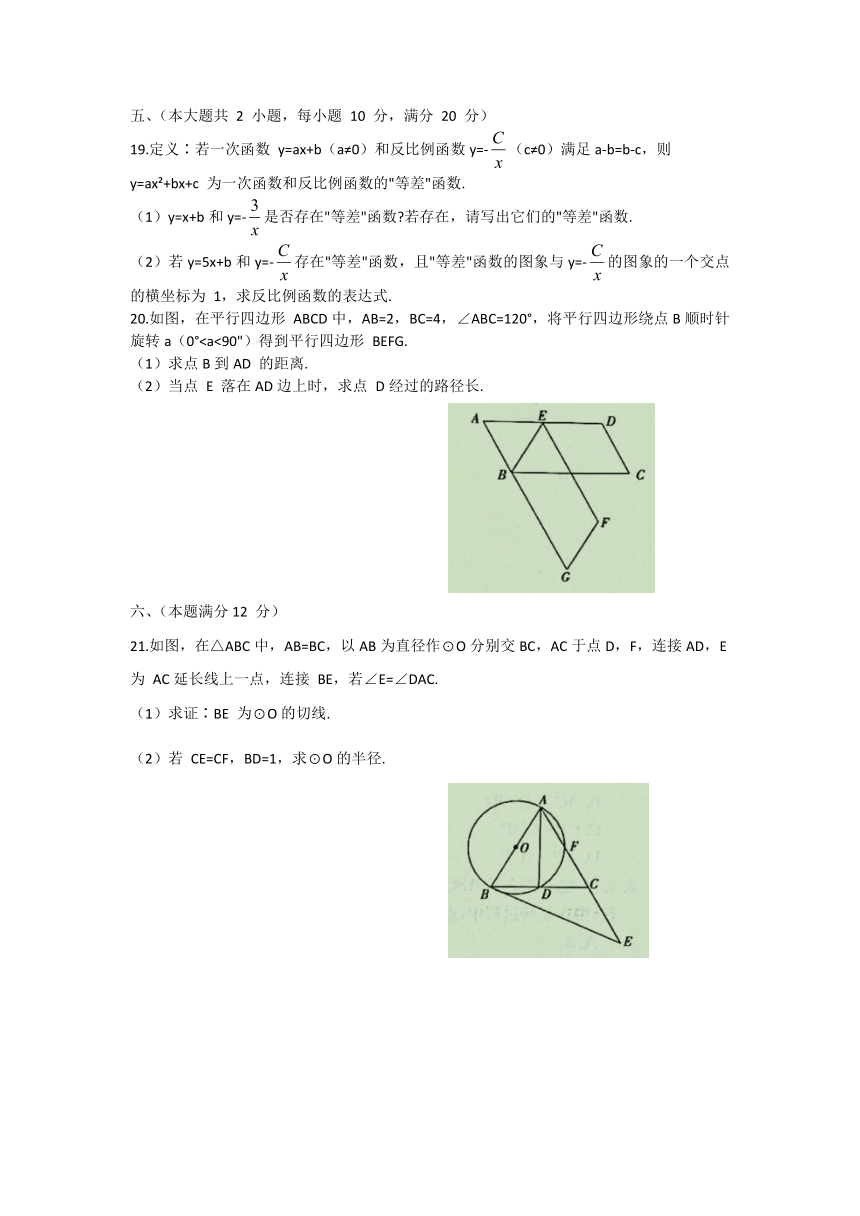
20.如图,在平行四边形
ABCD中,AB=2,BC=4,∠ABC=120°,将平行四边形绕点B顺时针
旋转a(0°BEFG.
(1)求点B到AD
的距离.
(2)当点
E
落在AD边上时,求点
D经过的路径长.
六、(本题满分12
分)
21.如图,在△ABC中,AB=BC,以AB为直径作⊙O分别交BC,AC于点D,F,连接AD,E为
AC延长线上一点,连接
BE,若∠E=∠DAC.
(1)求证∶BE
为⊙O的切线.
(2)若
CE=CF,BD=1,求⊙O的半径.
七、(本题满分
12
分)
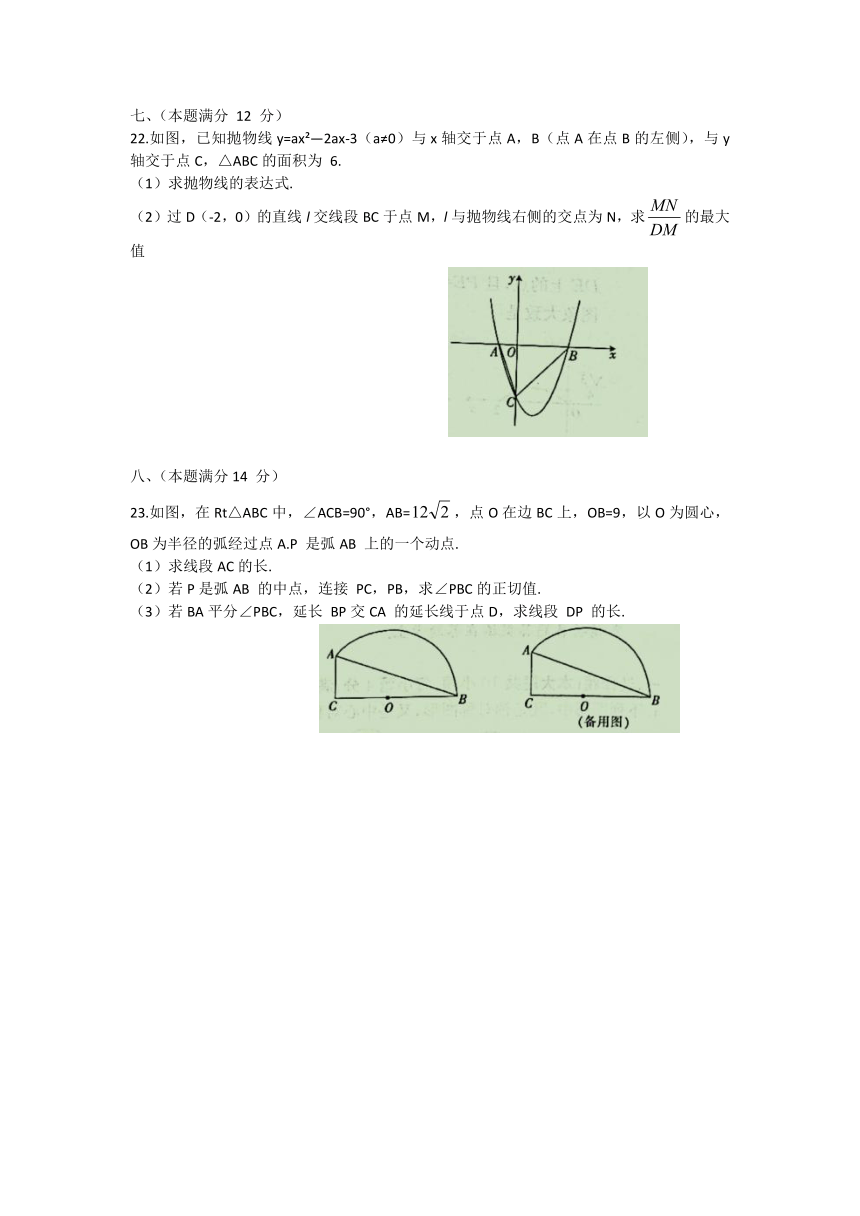
22.如图,已知抛物线y=ax?—2ax-3(a≠0)与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,△ABC的面积为
6.
(1)求抛物线的表达式.
(2)过D(-2,0)的直线l交线段BC于点M,l与抛物线右侧的交点为N,求的最大值
八、(本题满分14
分)
23.如图,在Rt△ABC中,∠ACB=90°,AB=,点O在边BC上,OB=9,以O为圆心,OB为半径的弧经过点A.P
是弧AB
上的一个动点.
(1)求线段AC的长.
(2)若P是弧AB
的中点,连接
PC,PB,求∠PBC的正切值.
(3)若BA平分∠PBC,延长
BP交CA
的延长线于点D,求线段
DP
的长.
2020~2021
学年度第一学期九年级数学期末质量监测试卷
考生注意;
本试卷共
150
分,考试时间
120
分钟.
2.
请将各题答案填在答题卡上.
一、选择题(本大题共
10
小题,每小题4分,满分
40
分)
1.下对度形中,既是轴对称图形,又是中心对称图形的是
2如图,PA
是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠BAP=116°则∠P的度
数为
A.64°
B.26°
52°
D.38°
3.共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,若第二个月的增长率是x,第三个月的增长率是第二个月的两倍,那么y与x的函数关系是
A.
y=a(1+x)(1+2x)
B.
y=a(1+x)2
C.
y=2a(1+x)2
D.
y=2x2+a
4已知点A(x,y)在反比例函数的图象上,若x>2,则y的取值范围是
A.3
y<3
C.
0
y>3
5.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与
AD
相交于点F.则图中与△ABD相似的是
A.△ABC
B.
△ABF
C.△BFD
D.
△AEF
6.如图,AB是⊙O的直径,C,D是上的三等分点,且sin∠ABC=,则∠A+∠D
等于
A.120°
B.95°
C.105°
D.150°
7.如图,AB是⊙O的直径,CD是弦,四边形OBCD是菱形,AC与OD
相交于点P,则下列结论错误的是
A.
OD⊥AC
B.AC平分OD
C
.CB=2DP
D.
AP=2OP
8.如图、已知正方形
ABCD与正方形
AEFG的边长分别为4和1,若将正方形
AEFG绕点A旋转,则在旋转过程中,点
C,E
之间的最小距离为
A.3
B.-1
C.
-1
D.
9.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在格点上,点E在AB的延长线上,以A为圆心,AE为半径画弧,交
AD的延长线于点F,且经过点C,则扇形
AEF
的面积为
A.π
B.π
C.π
D.π
10.如图,在矩形
ABCD中,AB=,BC=4,E为BC的中点,连接AE,DE,P,Q分别是AE,
DE上的点,且
PE=DQ.设△EPQ的面积为y,PE的长为z,则y关于x
的函数关系式的图象大致是
二、填空题(本大题共4
小题,每小题
5
分,满分
20
分)
11.在平面内,⊙O的半径为5cm,点P到圆心O的距离为6cm,则点P与⊙O的位置关系是_____.(填"圆内""圆外"或"圆上")
12.在平面直角坐标系中,点(-2,4)关于原点对称的点的坐标为___
13.圆锥的表面展开图由一个扇形和一个圆组成,已知扇形的半径为9,圆心角为120°,则圆锥的底面圆的半径为_____
14.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过点
A(0,4),B(-4,4),C(6,2).
(1)若该圆弧所在圆的圆心为D,则AD的长为
(2)该圆弧的长为___
三、(本大题共
2
小题,每小题
8
分,满分
16
分)
15.如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D,E重合),
求∠CPD的余角的度数。
16.如图,在等边△ABC中,D是边AC上的一点,连接
BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接
ED.若
BC=7,BD=6,求△AED的周长.
四、(本大题共
2
小题,每小题
8
分,满分
16
分)
17.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的△ABC,且∠B=90°
(1)将△ABC绕点O顺时针旋转
90°后得到△EFG(其中
A,B,C三点旋转后的对应点分别是E,F,G),画出△EFG.
(2)设△EFG的内切圆的半径为r,△EFG的外接圆的半径为R,则=
18.某校"综合与实践"小组采用无人机辅助的方法测量一座桥的长度.如图,桥
AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥
AB上方150米的点C处悬停,此时测得桥两端A,B两点的俯角分别为
65°和45°,求桥
AB的长度.(参考数据∶sin
65°≈0.91,
cos
65°≈0.42,tan
65°≈2.14;结果精确到
0.1米)
五、(本大题共
2
小题,每小题
10
分,满分
20
分)
19.定义∶若一次函数
y=ax+b(a≠0)和反比例函数y=-(c≠0)满足a-b=b-c,则
y=ax?+bx+c
为一次函数和反比例函数的"等差"函数.
(1)y=x+b和y=-是否存在"等差"函数?若存在,请写出它们的"等差"函数.
(2)若y=5x+b和y=-存在"等差"函数,且"等差"函数的图象与y=-的图象的一个交点的横坐标为
1,求反比例函数的表达式.
20.如图,在平行四边形
ABCD中,AB=2,BC=4,∠ABC=120°,将平行四边形绕点B顺时针
旋转a(0°
(1)求点B到AD
的距离.
(2)当点
E
落在AD边上时,求点
D经过的路径长.
六、(本题满分12
分)
21.如图,在△ABC中,AB=BC,以AB为直径作⊙O分别交BC,AC于点D,F,连接AD,E为
AC延长线上一点,连接
BE,若∠E=∠DAC.
(1)求证∶BE
为⊙O的切线.
(2)若
CE=CF,BD=1,求⊙O的半径.
七、(本题满分
12
分)
22.如图,已知抛物线y=ax?—2ax-3(a≠0)与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,△ABC的面积为
6.
(1)求抛物线的表达式.
(2)过D(-2,0)的直线l交线段BC于点M,l与抛物线右侧的交点为N,求的最大值
八、(本题满分14
分)
23.如图,在Rt△ABC中,∠ACB=90°,AB=,点O在边BC上,OB=9,以O为圆心,OB为半径的弧经过点A.P
是弧AB
上的一个动点.
(1)求线段AC的长.
(2)若P是弧AB
的中点,连接
PC,PB,求∠PBC的正切值.
(3)若BA平分∠PBC,延长
BP交CA
的延长线于点D,求线段
DP
的长.
同课章节目录
