_沪科版八年级数学下册课件-16.1 二次根式(17张)
文档属性
| 名称 | _沪科版八年级数学下册课件-16.1 二次根式(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 20:20:27 | ||
图片预览






文档简介
16.1 二次根式
求下面正方形的边长.
面积8
面积2
引入:
边长
边长
一般地,形如 的式子叫做二次根式.
(a≥0)
二次根式的定义
思考:
(1)二次根式与前面学习的算术平方根有什么关系?
(2)对于被开方数a有什么要求?
前面的学习中,我们遇到过这些式子
?
?
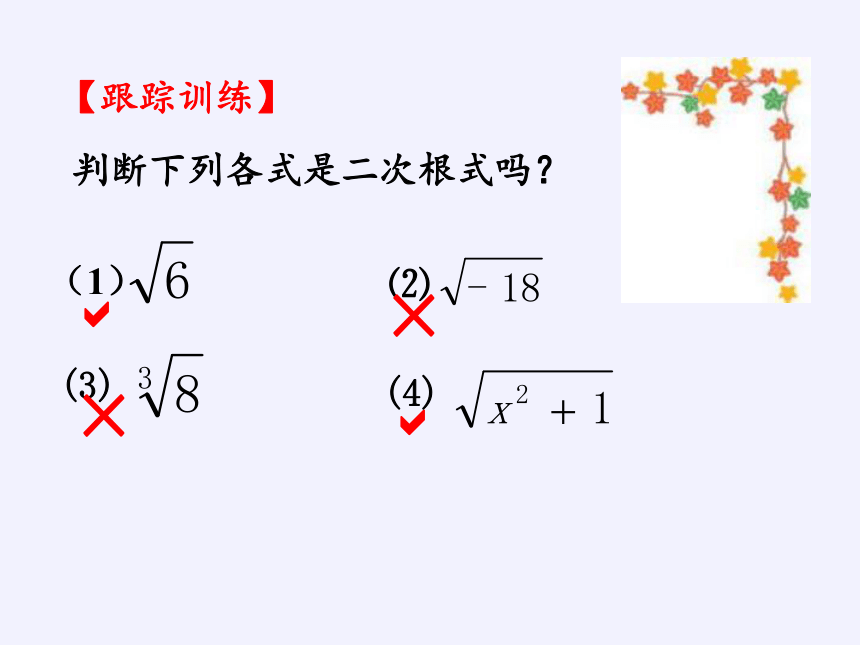
判断下列各式是二次根式吗?
【跟踪训练】
(1)
⑵
(3)
(4)
×
×
计算下列各式
6
6
20
20
合作探究一
= ,
= ;
(1)
(2)
(3)
,
.
5
5
猜想:你能得到什么结论?(用含字母的式子表示)
与
验证:下面式子是否相等,借助计算器验证.
结论:
积的算术平方根等于算术平方根的积.
问题:对于一切的实数a,b都成立吗?若不成立,请举反例说明。
想一想?
成立吗?为什么?
∵
∵
∴这个等式不成立.
注意:
a、b必须都是非负数!
积的算术平方根等于各因式算术平方根的积.
(a≥0,b≥0)
ab
=
.
,
,
;
计算下列各式, 观察计算结果,你发现什么结论?(用字母表示)
思考:
合作探究二
注意:
a必须是非负数!
b必须是正数!
商的算术平方根等于算术平方根的商.
(a≥0,b>0)
应用:结合性质,解决问题
我们把 这样的式子称为最简二次根式。
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式;
最简二次根式的定义
1、判断下列各式是否为最简二次根式?
(2) ( );
(3) ( );
(4) ( );
(1) ( );
×
×
×
√
【跟踪训练】
2、你能将(1)(2)(4)化简吗?
试一试。
在二次根式的运算中, 最后结果一般要求:
(1)写成最简二次根式的形式.
(2)分母中不含有根号.
【规律方法】
小结
通过今天的学习,
用你自己的话说说你的收获和体会?
两个概念:二次根式与最简二次根式
两个公式:
知识的升华
独立
作业
作业布置:
习题16.1第(1、2、4)题
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
谢 谢
求下面正方形的边长.
面积8
面积2
引入:
边长
边长
一般地,形如 的式子叫做二次根式.
(a≥0)
二次根式的定义
思考:
(1)二次根式与前面学习的算术平方根有什么关系?
(2)对于被开方数a有什么要求?
前面的学习中,我们遇到过这些式子
?
?
判断下列各式是二次根式吗?
【跟踪训练】
(1)
⑵
(3)
(4)
×
×
计算下列各式
6
6
20
20
合作探究一
= ,
= ;
(1)
(2)
(3)
,
.
5
5
猜想:你能得到什么结论?(用含字母的式子表示)
与
验证:下面式子是否相等,借助计算器验证.
结论:
积的算术平方根等于算术平方根的积.
问题:对于一切的实数a,b都成立吗?若不成立,请举反例说明。
想一想?
成立吗?为什么?
∵
∵
∴这个等式不成立.
注意:
a、b必须都是非负数!
积的算术平方根等于各因式算术平方根的积.
(a≥0,b≥0)
ab
=
.
,
,
;
计算下列各式, 观察计算结果,你发现什么结论?(用字母表示)
思考:
合作探究二
注意:
a必须是非负数!
b必须是正数!
商的算术平方根等于算术平方根的商.
(a≥0,b>0)
应用:结合性质,解决问题
我们把 这样的式子称为最简二次根式。
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式;
最简二次根式的定义
1、判断下列各式是否为最简二次根式?
(2) ( );
(3) ( );
(4) ( );
(1) ( );
×
×
×
√
【跟踪训练】
2、你能将(1)(2)(4)化简吗?
试一试。
在二次根式的运算中, 最后结果一般要求:
(1)写成最简二次根式的形式.
(2)分母中不含有根号.
【规律方法】
小结
通过今天的学习,
用你自己的话说说你的收获和体会?
两个概念:二次根式与最简二次根式
两个公式:
知识的升华
独立
作业
作业布置:
习题16.1第(1、2、4)题
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
谢 谢
