2020—2021学年北师大版七年级数学下册 第2章 平行线与相交线 综合训练(Word版 无答案)
文档属性
| 名称 | 2020—2021学年北师大版七年级数学下册 第2章 平行线与相交线 综合训练(Word版 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 20:47:46 | ||
图片预览

文档简介
平行线的性质和判定_习题综合训练
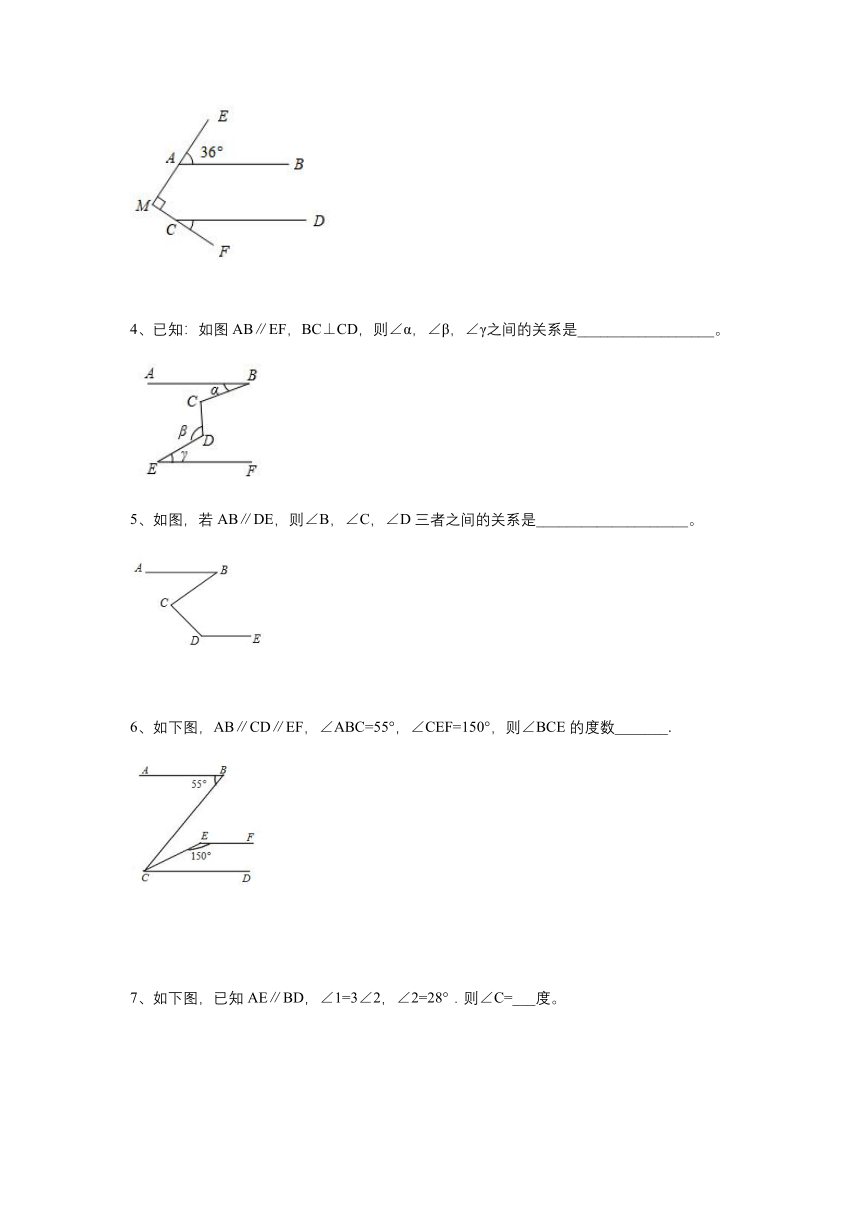
1、如图,AB∥CD,则∠B,∠E,∠F,∠G,∠D之间的关系是__________________。
2、细观察,找规律。
下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2=_______度,
图②中的∠A1+∠A2+∠A3=_______度,
图③中的∠A1+∠A2+∠A3+∠A4=_____度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=_______度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=__________度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1=__________度。
3、如图,AB∥CD,ME⊥MF,∠EAB=36°,则∠FCD=_______度.
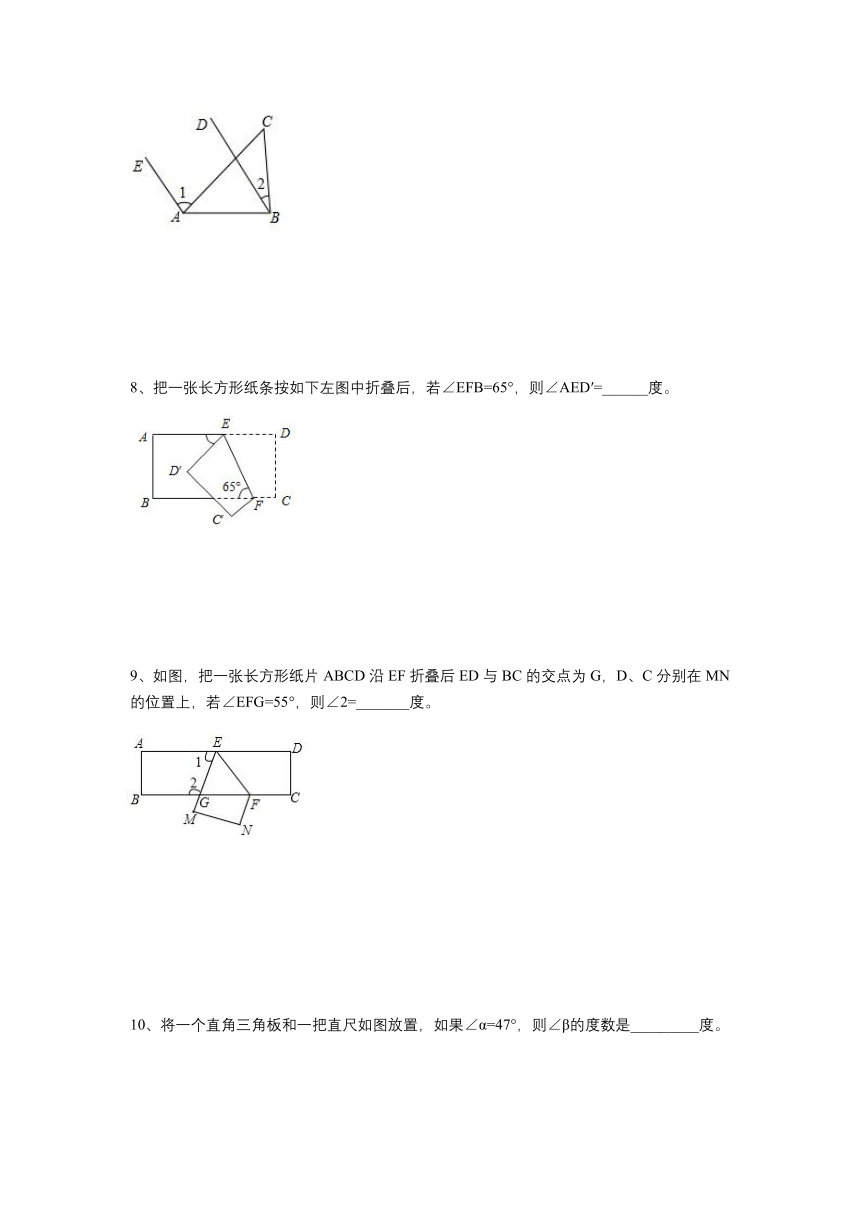
4、已知:如图AB∥EF,BC⊥CD,则∠α,∠β,∠γ之间的关系是__________________。
5、如图,若AB∥DE,则∠B,∠C,∠D三者之间的关系是____________________。
6、如下图,AB∥CD∥EF,∠ABC=55°,∠CEF=150°,则∠BCE的度数_______.
7、如下图,已知AE∥BD,∠1=3∠2,∠2=28°.则∠C=___度。
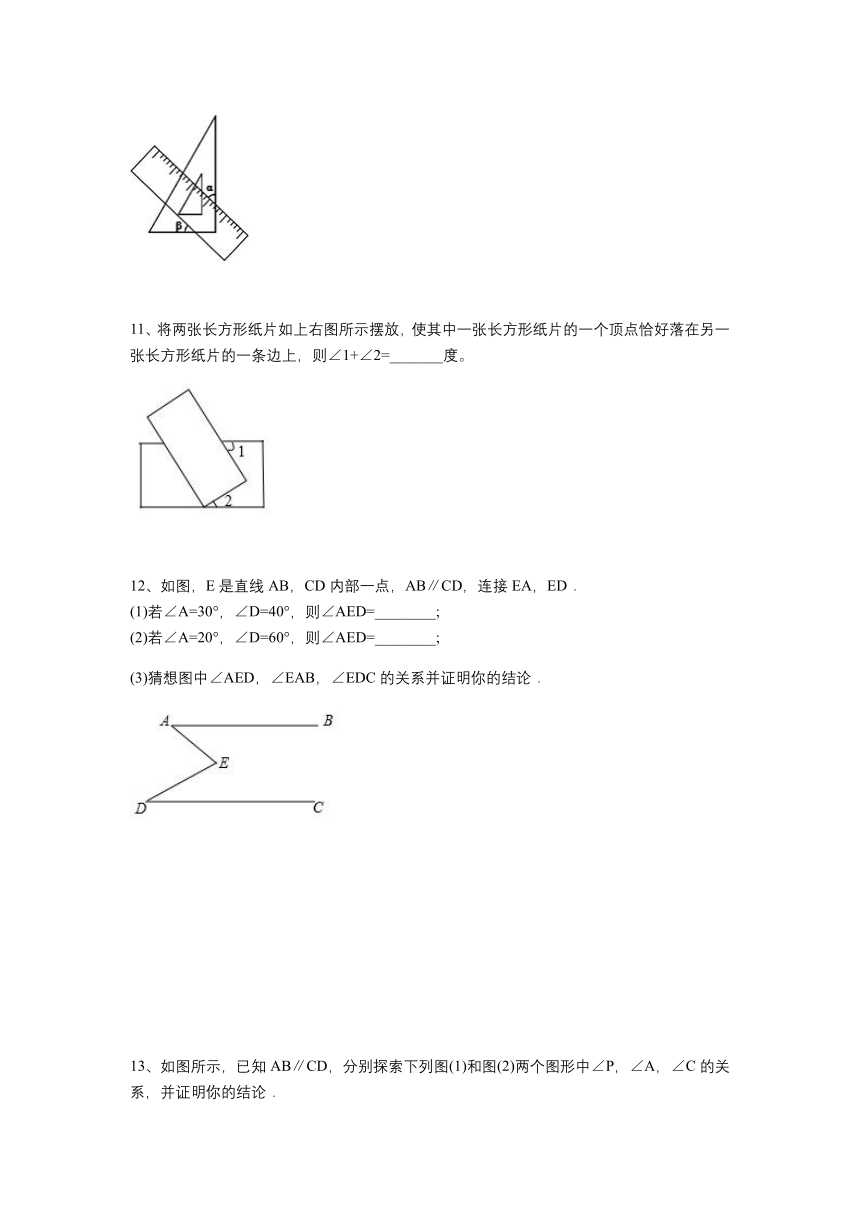
8、把一张长方形纸条按如下左图中折叠后,若∠EFB=65°,则∠AED′=______度。
9、如图,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=_______度。
10、将一个直角三角板和一把直尺如图放置,如果∠α=47°,则∠β的度数是_________度。
11、将两张长方形纸片如上右图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2=_______度。
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)若∠A=30°,∠D=40°,则∠AED=________;
(2)若∠A=20°,∠D=60°,则∠AED=________;
(3)猜想图中∠AED,∠EAB,∠EDC的关系并证明你的结论.
13、如图所示,已知AB∥CD,分别探索下列图(1)和图(2)两个图形中∠P,∠A,∠C的关系,并证明你的结论.
14、如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF⊥BC,AD⊥BC (已知)
∴∠BFE=90°,∠BDA=90°__________
即∠BFE=∠BDA
∴EF∥AD__________
∴∠2=__________.
又∵∠1=∠2(已知),
∴∠1=∠3.__________
∴AB∥__________,
∴∠BAC+__________=180°.
又∵∠BAC=70°(已知),
∴∠AGD=__________.
15、如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.
解:∵EF∥AD(已知)
∴∠2=(
__________
)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥
__________
?(
__________
)?
∴∠BAC+
__________
=180°(
__________
?)
又∵∠BAC=87°(已知)
∴∠AGD=
__________
?(等式的性质)
16、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:
解:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGB=90°
__________
∴∠ADC+∠EGB=180°
__________
∴AD∥EG
__________
∴∠1=∠2
__________
__________
=∠3
__________
又∵∠E=∠1(已知)
∴
__________
=
__________
(
__________
)
∴AD平分∠BAC
__________
.
17、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG//AC________
∴∠2=_________
∵∠1=∠2__________
∴∠1=∠DCA(等量代换)
∴EF//CD__________
∴∠AEF=∠ADC__________
∵EF⊥AB(已知)
∴∠AEF=90°__________
∴∠ADC=90°
∴CD⊥AB__________
18、填写下列证明过程中的推理根据:已知:如图所示,AC,BD相交于O,DF平分∠CDO与AC相交于F,BE平分∠ABO与AC相交于E,∠A=∠C.
求证:∠1=∠2.
证明:∵∠A=∠C(__________),
∴AB∥CD(__________).
∴∠ABO=∠CDO(__________).
又∵∠1=∠CDO,∠2=∠ABO(__________),
∴∠1=∠2(__________).
19、如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.求证:∠A=∠C.
证明:∵BE、DF分别平分∠ABC、∠ADC(已知)
∴∠1=∠ABC,∠3=∠ADC(__________)
∵∠ABC=∠ADC(已知)
∴∠ABC=∠ADC(__________)
∴∠1=∠3(__________)
∵∠1=∠2(已知)
∴∠2=∠3(等量代换)
∴(__________)∥(__________)(__________)
∴∠A+∠__________=180°,∠C+∠__________=180°(__________)
∴∠A=∠C(等量代换).
20、已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
21、如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
22、如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.
1、如图,AB∥CD,则∠B,∠E,∠F,∠G,∠D之间的关系是__________________。
2、细观察,找规律。
下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2=_______度,
图②中的∠A1+∠A2+∠A3=_______度,
图③中的∠A1+∠A2+∠A3+∠A4=_____度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=_______度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=__________度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1=__________度。
3、如图,AB∥CD,ME⊥MF,∠EAB=36°,则∠FCD=_______度.
4、已知:如图AB∥EF,BC⊥CD,则∠α,∠β,∠γ之间的关系是__________________。
5、如图,若AB∥DE,则∠B,∠C,∠D三者之间的关系是____________________。
6、如下图,AB∥CD∥EF,∠ABC=55°,∠CEF=150°,则∠BCE的度数_______.
7、如下图,已知AE∥BD,∠1=3∠2,∠2=28°.则∠C=___度。
8、把一张长方形纸条按如下左图中折叠后,若∠EFB=65°,则∠AED′=______度。
9、如图,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=_______度。
10、将一个直角三角板和一把直尺如图放置,如果∠α=47°,则∠β的度数是_________度。
11、将两张长方形纸片如上右图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2=_______度。
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)若∠A=30°,∠D=40°,则∠AED=________;
(2)若∠A=20°,∠D=60°,则∠AED=________;
(3)猜想图中∠AED,∠EAB,∠EDC的关系并证明你的结论.
13、如图所示,已知AB∥CD,分别探索下列图(1)和图(2)两个图形中∠P,∠A,∠C的关系,并证明你的结论.
14、如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF⊥BC,AD⊥BC (已知)
∴∠BFE=90°,∠BDA=90°__________
即∠BFE=∠BDA
∴EF∥AD__________
∴∠2=__________.
又∵∠1=∠2(已知),
∴∠1=∠3.__________
∴AB∥__________,
∴∠BAC+__________=180°.
又∵∠BAC=70°(已知),
∴∠AGD=__________.
15、如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.
解:∵EF∥AD(已知)
∴∠2=(
__________
)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥
__________
?(
__________
)?
∴∠BAC+
__________
=180°(
__________
?)
又∵∠BAC=87°(已知)
∴∠AGD=
__________
?(等式的性质)
16、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:
解:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGB=90°
__________
∴∠ADC+∠EGB=180°
__________
∴AD∥EG
__________
∴∠1=∠2
__________
__________
=∠3
__________
又∵∠E=∠1(已知)
∴
__________
=
__________
(
__________
)
∴AD平分∠BAC
__________
.
17、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG//AC________
∴∠2=_________
∵∠1=∠2__________
∴∠1=∠DCA(等量代换)
∴EF//CD__________
∴∠AEF=∠ADC__________
∵EF⊥AB(已知)
∴∠AEF=90°__________
∴∠ADC=90°
∴CD⊥AB__________
18、填写下列证明过程中的推理根据:已知:如图所示,AC,BD相交于O,DF平分∠CDO与AC相交于F,BE平分∠ABO与AC相交于E,∠A=∠C.
求证:∠1=∠2.
证明:∵∠A=∠C(__________),
∴AB∥CD(__________).
∴∠ABO=∠CDO(__________).
又∵∠1=∠CDO,∠2=∠ABO(__________),
∴∠1=∠2(__________).
19、如图,已知,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.求证:∠A=∠C.
证明:∵BE、DF分别平分∠ABC、∠ADC(已知)
∴∠1=∠ABC,∠3=∠ADC(__________)
∵∠ABC=∠ADC(已知)
∴∠ABC=∠ADC(__________)
∴∠1=∠3(__________)
∵∠1=∠2(已知)
∴∠2=∠3(等量代换)
∴(__________)∥(__________)(__________)
∴∠A+∠__________=180°,∠C+∠__________=180°(__________)
∴∠A=∠C(等量代换).
20、已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
21、如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
22、如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
