7.4 认识三角形(第2课时)(共32张PPT)
文档属性
| 名称 | 7.4 认识三角形(第2课时)(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 16:34:04 | ||
图片预览









文档简介
7.4 认识三角形
第2课时
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
找一找图中的三角形,并把它们勾画出来.
你还能举出一些实例吗?
新课导入
你对小学所学的三角形内容有什么回忆?
说一说
不在同一直线上的三条线段首尾相接所构成的图形叫作三角形(triangle).
三角形可用符号“△” 来表示, 如图2-2三角形可记作“△ABC”,读作“三角形ABC”. 其中,点A,B,C叫作△ABC的顶点; ∠A, ∠B, ∠C叫作△ABC的内角(简称△ABC的角);线段AB, BC, CA叫作△ABC的边.通常∠A, ∠B, ∠C的对边BC, AC, AB 可分别
用a, b, c来表示.
A
B
C
a
b
c
图2-2
我们如何来研究三角形?
三角形如何分类呢?
三角形按边如何分类呢?
探究
两条边相等的三角形叫作等腰三角形. 在等腰三角形中,相等的两边叫作腰,另外一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角,如图2-3.
三边都相等的三角形叫作等边三角形(或正三角形). 等边三角形是特殊的等腰三角形—腰和底边相等的等腰三角形,如图2-4.
A
B
C
A
B
C
顶
角
等腰三角形
图2-3
底角
底角
底边
腰
腰
等边三角形
图2-4
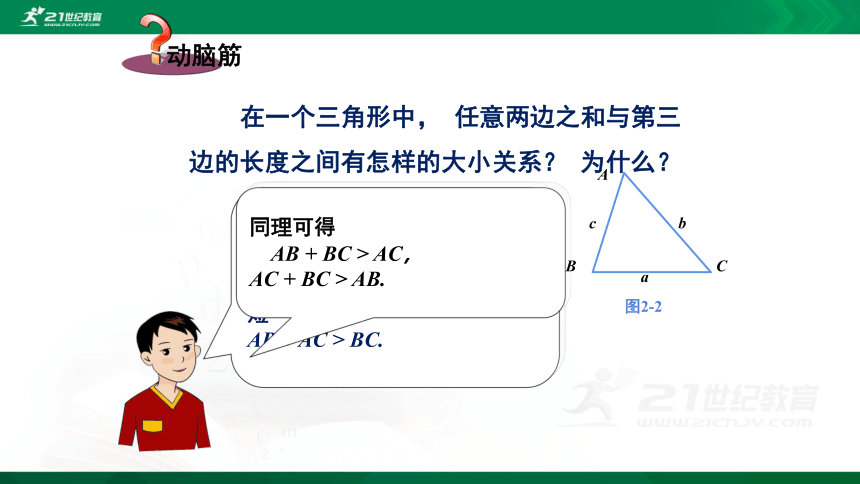
在一个三角形中, 任意两边之和与第三边的长度之间有怎样的大小关系? 为什么?
动脑筋
如图2-2, 在△ABC中, BC是连接B, C两点的一条线段, 由基本事实“两点之间线段最短” 可得
AB + AC > BC.
同理可得
AB + BC > AC,
AC + BC > AB.
A
B
C
a
b
c
图2-2
结论
三角形的任意两边之和大于第三边.
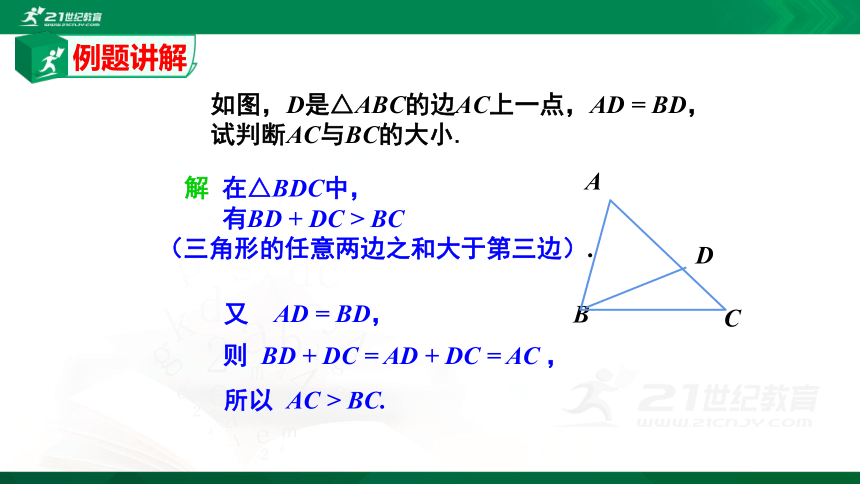
如图,D是△ABC的边AC上一点,AD = BD,试判断AC与BC的大小.
A
B
C
D
解 在△BDC中,
有BD + DC > BC
(三角形的任意两边之和大于第三边).
所以 AC > BC.
又 AD = BD,
则 BD + DC = AD + DC = AC ,
例题讲解
练习
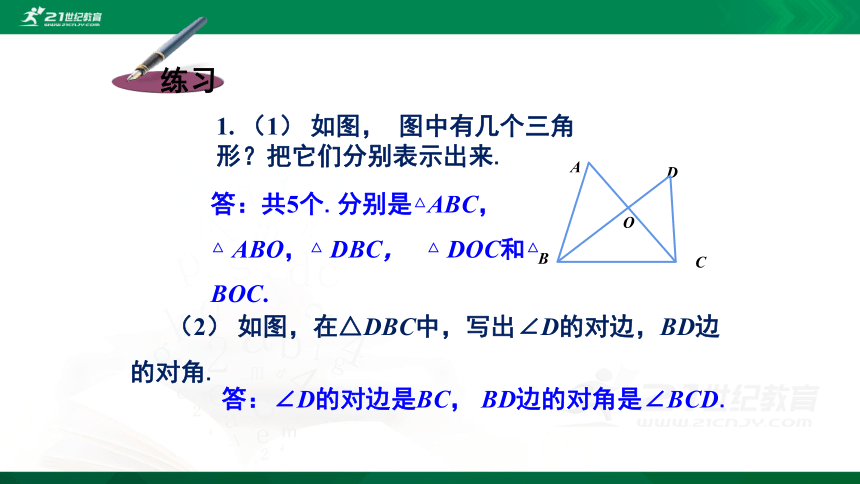
1. (1) 如图, 图中有几个三角 形?把它们分别表示出来.
(2) 如图,在△DBC中,写出∠D的对边,BD边的对角.
A
B
C
D
O
答:共5个.分别是△ABC,
△ ABO,△ DBC, △ DOC和△ BOC.
答:∠D的对边是BC, BD边的对角是∠BCD.
2. 三根长分别为2 cm,5 cm,6 cm的小木棒能首尾相接构成一个三角形吗?
答:能构成一个三角形.
因为“三角形的任意两边之和大于第三边”
2+5=7>6,所以能构成一个三角形.
等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )
A.16 B.18 C.20 D.16或20
解析
分类讨论:①当4是底边长时,周长为8+8+4=20;②当8是底边长时,周长为4+4+8=16;再由三角形的任意两边和大于第三边,确定三角形的第三边长, ②不符合.
C
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median).
三角形的“中线”
BE=EC
B
C
AE是BC边上的中线.
E
A
BE=EC
B
C
(1) 在纸上画出一个锐角三角形,
并画出它的三条中线,
议一议
它们有怎样的位置关系?
(2) 钝角三角形和直角三角形的中线又是怎样的?
E
A
A
C
B
F
E
D
O
则AB边上的中线是:
AC边上的中线是:
CF
BE
AD
∵BE是中线
∴ ____=____ =
∴AB=2____=2____
∵CF是中线
AE
CE
AF
BF
BC边上的中线是:
AC
如图,点D、E、F分别是边BC、AC、AB上的中点
三角形的三条中线交于一点.
2、你还能得到那些结论?
1、 思考:任意三角形的三条中线的交点都在三角形的内部吗?
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线吗?
试一试
B
A
C
1、用圆规画最简便.
2、将纸上画出的三角形剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的角平分线.
A
B
C
A
D
三形的角平分线的定义
B
A
C
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的一个角的平分线叫做三角形的角平分线.这句话对吗?
D
∠1=∠2
1
2
“三角形的角平分线”是一条线段
三角形的角平分线的性质
每人准备锐角三角形、钝角三角形和直角三角形纸片
各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗?
(2) 你能用折纸的办法得到它们吗?
(3) 在每个三角形中,这三条角平分线之间有怎样的
位置关系?
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴_____ =_____ = _____
∴∠ACB=2______=2_____
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的三条角平分线线交于一点
三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高.
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
一块三角形的煎饼,要把它分成面积大小相同的6块应怎样分?你有多少种分法?如果限定只能切三刀呢?
思考
1.图中共有几个三角形?把它们分别表示出来,并用量角器检验它们是锐角三角形、直角三角形,还是钝角三角形.
5个三角形.
△ABC、△ ADC、△ADE、△ADB、△EDB.
锐角三角形有△ADE,
直角三角形有△ABC、△ ADC,
钝角三角形有△ADB、△EDB.
课堂练习
2.4根小木棒的长度分别为2cm、3cm、
4cm和5cm.用其中3根搭三角形,可
以搭出几个不同的三角形?
满足两边之和大于第三边,两边之差小于第三边即可搭出三角形,有2cm、3cm、4cm组合,有3cm、4cm和5cm组合,有2cm、4cm和5cm组合,共3个不同的三角形.
3.剪一张三角形纸片,用折纸的方法折出这个三角形的3条角平分线.你有什么发现?
3条角平分线交于一点.
4.分别画出图中各个三角形的3条中线.你有什么发现?
3条中线交于一点.
5.分别画出图中各个三角形的3条高.你有什么发现?
3条高线交于一点.
6、图中以BC为边的三角形共有______个;它们分别___________________________________.
在△ABD中,∠A是______边的对角, ∠ADB是△_____的内角,又是________________的一个外角.
D
B
E
C
F
A
4
△BCF; △ BCE; △ BCD; △ BCA
△FDC 或△BDC
ABD
BD
1. 这节课我们研究的是什么?怎么研究的?
2. 进一步我们要研究三角形的哪些元素?
课堂小结
谢谢聆听
第2课时
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
找一找图中的三角形,并把它们勾画出来.
你还能举出一些实例吗?
新课导入
你对小学所学的三角形内容有什么回忆?
说一说
不在同一直线上的三条线段首尾相接所构成的图形叫作三角形(triangle).
三角形可用符号“△” 来表示, 如图2-2三角形可记作“△ABC”,读作“三角形ABC”. 其中,点A,B,C叫作△ABC的顶点; ∠A, ∠B, ∠C叫作△ABC的内角(简称△ABC的角);线段AB, BC, CA叫作△ABC的边.通常∠A, ∠B, ∠C的对边BC, AC, AB 可分别
用a, b, c来表示.
A
B
C
a
b
c
图2-2
我们如何来研究三角形?
三角形如何分类呢?
三角形按边如何分类呢?
探究
两条边相等的三角形叫作等腰三角形. 在等腰三角形中,相等的两边叫作腰,另外一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角,如图2-3.
三边都相等的三角形叫作等边三角形(或正三角形). 等边三角形是特殊的等腰三角形—腰和底边相等的等腰三角形,如图2-4.
A
B
C
A
B
C
顶
角
等腰三角形
图2-3
底角
底角
底边
腰
腰
等边三角形
图2-4
在一个三角形中, 任意两边之和与第三边的长度之间有怎样的大小关系? 为什么?
动脑筋
如图2-2, 在△ABC中, BC是连接B, C两点的一条线段, 由基本事实“两点之间线段最短” 可得
AB + AC > BC.
同理可得
AB + BC > AC,
AC + BC > AB.
A
B
C
a
b
c
图2-2
结论
三角形的任意两边之和大于第三边.
如图,D是△ABC的边AC上一点,AD = BD,试判断AC与BC的大小.
A
B
C
D
解 在△BDC中,
有BD + DC > BC
(三角形的任意两边之和大于第三边).
所以 AC > BC.
又 AD = BD,
则 BD + DC = AD + DC = AC ,
例题讲解
练习
1. (1) 如图, 图中有几个三角 形?把它们分别表示出来.
(2) 如图,在△DBC中,写出∠D的对边,BD边的对角.
A
B
C
D
O
答:共5个.分别是△ABC,
△ ABO,△ DBC, △ DOC和△ BOC.
答:∠D的对边是BC, BD边的对角是∠BCD.
2. 三根长分别为2 cm,5 cm,6 cm的小木棒能首尾相接构成一个三角形吗?
答:能构成一个三角形.
因为“三角形的任意两边之和大于第三边”
2+5=7>6,所以能构成一个三角形.
等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )
A.16 B.18 C.20 D.16或20
解析
分类讨论:①当4是底边长时,周长为8+8+4=20;②当8是底边长时,周长为4+4+8=16;再由三角形的任意两边和大于第三边,确定三角形的第三边长, ②不符合.
C
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median).
三角形的“中线”
BE=EC
B
C
AE是BC边上的中线.
E
A
BE=EC
B
C
(1) 在纸上画出一个锐角三角形,
并画出它的三条中线,
议一议
它们有怎样的位置关系?
(2) 钝角三角形和直角三角形的中线又是怎样的?
E
A
A
C
B
F
E
D
O
则AB边上的中线是:
AC边上的中线是:
CF
BE
AD
∵BE是中线
∴ ____=____ =
∴AB=2____=2____
∵CF是中线
AE
CE
AF
BF
BC边上的中线是:
AC
如图,点D、E、F分别是边BC、AC、AB上的中点
三角形的三条中线交于一点.
2、你还能得到那些结论?
1、 思考:任意三角形的三条中线的交点都在三角形的内部吗?
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线吗?
试一试
B
A
C
1、用圆规画最简便.
2、将纸上画出的三角形剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的角平分线.
A
B
C
A
D
三形的角平分线的定义
B
A
C
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的一个角的平分线叫做三角形的角平分线.这句话对吗?
D
∠1=∠2
1
2
“三角形的角平分线”是一条线段
三角形的角平分线的性质
每人准备锐角三角形、钝角三角形和直角三角形纸片
各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗?
(2) 你能用折纸的办法得到它们吗?
(3) 在每个三角形中,这三条角平分线之间有怎样的
位置关系?
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴_____ =_____ = _____
∴∠ACB=2______=2_____
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的三条角平分线线交于一点
三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高.
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
一块三角形的煎饼,要把它分成面积大小相同的6块应怎样分?你有多少种分法?如果限定只能切三刀呢?
思考
1.图中共有几个三角形?把它们分别表示出来,并用量角器检验它们是锐角三角形、直角三角形,还是钝角三角形.
5个三角形.
△ABC、△ ADC、△ADE、△ADB、△EDB.
锐角三角形有△ADE,
直角三角形有△ABC、△ ADC,
钝角三角形有△ADB、△EDB.
课堂练习
2.4根小木棒的长度分别为2cm、3cm、
4cm和5cm.用其中3根搭三角形,可
以搭出几个不同的三角形?
满足两边之和大于第三边,两边之差小于第三边即可搭出三角形,有2cm、3cm、4cm组合,有3cm、4cm和5cm组合,有2cm、4cm和5cm组合,共3个不同的三角形.
3.剪一张三角形纸片,用折纸的方法折出这个三角形的3条角平分线.你有什么发现?
3条角平分线交于一点.
4.分别画出图中各个三角形的3条中线.你有什么发现?
3条中线交于一点.
5.分别画出图中各个三角形的3条高.你有什么发现?
3条高线交于一点.
6、图中以BC为边的三角形共有______个;它们分别___________________________________.
在△ABD中,∠A是______边的对角, ∠ADB是△_____的内角,又是________________的一个外角.
D
B
E
C
F
A
4
△BCF; △ BCE; △ BCD; △ BCA
△FDC 或△BDC
ABD
BD
1. 这节课我们研究的是什么?怎么研究的?
2. 进一步我们要研究三角形的哪些元素?
课堂小结
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
